МОДЕЛИРОВАНИЕ  ДИФРАКЦИИ  ВОЛН  НА  ПОВЕРХНОСТИ  ВЯЗКОЙ  ЖИДКОСТИ  КРУГОВЫМ  ЦИЛИНДРОМ

Сычева  Елена  Михайловна

лаборант  кафедры  математического  моделирования  Института  Математики  и  Компьютерных  Наук  Тюменского  Государственного  Университета,

магистрант  кафедры  математического  моделирования  Тюменского  государственного  университета,  РФ,  г.  Тюмень

E-mail:  

MODELING  OF  THE  WAVE  DIFFRACTION  ON  THE  VISCOUS  LIQUID  SURFACE  BY  A  ROUND  CYLINDER

Sycheva  Elena

A  laboratory  assistant  of  the  Mathematical  Modeling  Department,  Institute  of  Mathematics  and  Computer  Science,  Tyumen  State  University,

a  Master  student  of  the  Mathematical  Modeling  Department,  Tyumen  State  University,  Russia,  Tyumen

АННОТАЦИЯ

Рассматривается  движение  жидкости,  вызванное  взаимодействием  набегающей  гравитационной  волны,  распространяющейся  на  поверхности  слоя  вязкой  несжимаемой  жидкости,  с  круговым  цилиндром  бесконечной  длины.  Получено  решение  задачи  для  колебаний  малой  амплитуды.

ABSTRACT

We  shall  consider  the  motion  of  liquid,  caused  by  the  interaction  of  incoming  gravitational  wave,  spreading  on  the  surface  of  the  viscous  incompressible  liquid  coat  with  an  infinitely  long  round  cylinder.  The  problem  was  solved  for  the  case  of  small  oscillations.

Ключевые  слова :  дифракция;  вязкость;  волновые  движения  жидкости.

Keywords :  diffraction;  viscosity;  wave  motion  of  liquid.

В  области  занятой  жидкостью,  выполняются  уравнение  неразрывности  и  уравнения  движения:

где:    —  вектор  скорости, 

  —  плотность, 

P  —  давление, 

  —  динамический  коэффициент  вязкости, 

  —  вектор  силы  тяжести.

При  заглублении  скорость  жидкости  должна  затухать,  т.  е.  выполнено  условие

На  свободной  поверхности    задаются  кинематическое  условие  [1]

и  динамические  условия  [2]

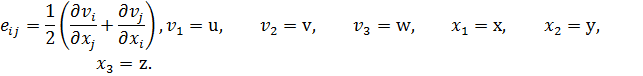
Здесь    —  постоянное  атмосферное  давление.

На  поверхности  цилиндра  S  в  случае  вязкой  жидкости  должно  выполняться  условие  прилипания:

Будем  рассматривать  колебания  с  амплитудой  весьма  малой  по  сравнению  с  длиной  волны.  Тогда  система  уравнений  и  граничных  условий  примет  вид:

                                (1)

    (2)

                   (3)

                                         (4)

где:    —  динамическое  давление, 

  —  кинематический  коэффициент  вязкости.

Решение  задачи  необходимо  искать  в  виде  суммы  потенциальной  и  вихревой  составляющей.  Исходя  из  этого,  представим  скорость  в  виде  [3]:

где:    —  потенциал, 

  —  векторная  функция  тока.

Тогда  применяя  к  уравнениям  (1)  операции  div  и  rot  их  можно  свести  к  системе  уравнений

Применяя  операции  дифференцирования  к  уравнениям  для  функции    и  компонент  векторной  функции  ,  получим  уравнения  для  вертикальной  составляющей  скорости 

                                  (5)

Граничные  условия  (2)  с  помощью  операций  дифференцирования  и  уравнений  (1)  преобразуются  к  виду

     (6)

                                 (7)

Из  условия  (3)  получим

                                  (8)

а  из  условия  затухания  волнового  движения  при  заглублении  (4):

                                         (9)

Таким  образом,  исходная  волновая  задача  сведена  к  задаче  для  вертикальной  составляющей  скорости  (5)—(9). 

Волновое  движение  жидкости  для  свободной  волны,  не  искаженной  препятствием,  описывается  следующими  функциями  [4]

,

где:    —  волновое  число, 

  —  длина  волны,  ,  , 

  —  направление  распространения  волны,  отсчитываемое  от  оси    в  горизонтальной  плоскости, 

  —  комплексная  частота,  для  которой  получено  дисперсионное  уравнение

Далее  будем  рассматривать  дифракцию  набегающей  волны  круговым  цилиндром  с  вертикальными  образующими.  Функции    и    будем  искать  в  виде

.

Выражения  для  функций  и    через    примут  следующий  вид:

Из  уравнений  (5)  вытекает  следующее  уравнение  Гельмгольца  для  функции 

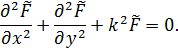
Условия  (6),  (7)  и  (9)  при  таком  представлении  для    и    выполняются,  а  из  условия  (8)  следует  условие  для 

где    —  контур  сечения  препятствия  горизонтальной  плоскостью.

Функцию    можно  представить  в  виде

где  первое  слагаемое    соответствует  набегающей  волне,  а  второе  характеризует  возмущенное  движение  жидкости.

Уравнение  Гельмгольца  для  определения  функции    и  условие  на  контуре    в  полярных  координатах  принимают  вид

                   (10)

                                   (11)

где    —  радиус  цилиндра.

Функция  ,  как  решение  уравнения  Гельмгольца,  должна  также  удовлетворять  условию  излучения  в  форме  [5]

Решение  уравнения  (10)  будем  искать  с  помощью  метода  разделения  переменных,  представив  неизвестную  функцию  в  виде

Подставив  последнее  выражение  в  уравнение  и  проведя  разделение  переменных,  получим  уравнения

где    —  константа  разделения. 

Решение  второго  уравнения,  удовлетворяющее  условию  периодичности  по    и  условию  симметрии  относительно  ,  имеет  вид 

где    —  целое  число.

Условию  излучения  удовлетворяет  функция  Ханкеля  первого  рода

Тогда  функция    примет  вид

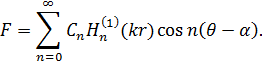
Коэффициенты    определим  из  условия  (11).  Для  этого  используем  разложение  [6]

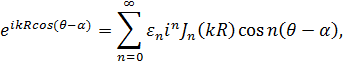
где    —  функция  Бесселя  первого  рода, 

Тогда  получим

В  случае  малого  значения  числа    (длина  волны  много  больше  радиуса  цилиндра)  условие  на  контуре    можно  записать  в  виде

Тогда  функция  ,  определяющая  суммарное  волновое  поле,  равна 

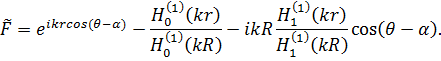
Список  литературы:

1.Кочин  Н.Е.,  Кибель  И.А.,  Розе  Н.В.  Теоретическая  гидромеханика.  Ч.  2.  М.:  Физматгиз.,  1963.  —  728  с.

2.Бэтчелор  Дж.  Введение  в  динамику  жидкости.  М.:  Мир,  1973.  —  792  с.

3.Баринов  В.А.,  Басинский  К.Ю.  Моделирование  волновых  движений  вязкой  жидкости  //  Вестник  Тюмен.  ун-та.  —  2009.  —  №  6.  —  С.  144—151.

4.Левич  В.Г.  Физико-химическая  гидродинамика.  М.:  Физматгиз,  1959.  —  700  с.

5.Кочин  Н.Е.  Собр.  Соч.  Т.  2.  М.;  Л.,  1949,  —  305  с.

6.Градштейн  И.С.,  Рыжик  И.М.  Таблицы  интегралов,  сумм,  рядов  и  произведений.  М.,  1963.  —  1100  с.