ПОСТРОЕНИЕ  ТРЕХМЕРНЫХ  СЕТОК  ОКОЛО  КРЫЛА  С  КРУТКОЙ  ДЛЯ  РАСЧЕТА  ТРАНСЗВУКОВОГО  ОБТЕКАНИЯ

Рябинин  Анатолий  Николаевич

д-р  физ.-мат.  наук,  гл.  научн.  сотр.  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт- Петербург

E-mail:  a _ryabinin@front.ru

GENERATION  OF  3D  MESHES  NEAR  THE  TWISTED  WING  FOR  CALCULATION  OF  TRANSONIC  FLOW

Ryabinin  Anatoly

D.Sc,  Principal  Researcher,  St.  Petersburg  State  University,  Russia,  St.  Petersburg

Настоящая  работа  поддержана  РФФИ,  грант  №  13-08-00288.  Исследования  были  проведены  с  использованием  вычислительных  ресурсов  Ресурсного  Центра  "Вычислительный  центр  СПбГУ"  ( http://cc.spbu.ru).

АННОТАЦИЯ

Описан  алгоритм  построения  трехмерной  расчетной  сетки  для  расчета  обтекания  крыльев,  использующей  вытянутые  вдоль  размаха  крыла  элементы.  Приведен  пример  расчета  трансзвукового  обтекания  сегмента  крыла  J78  с  круткой. 

ABSTRACT

An  algorithm  for  generation  a  three-dimensional  grid  is  described  for  the  calculation  of  flow  past  the  wings,  using  elongated  spanwise  elements.  An  example  of  calculation  of  transonic  flow  past  the  segment  of  J78  twisted  wing  is  presented.

Ключевые  слова:   численный  расчет;  крыло;  транзвуковое  течение;  построение  сетки.

Keywords:   numerical  calculation;  wing;  transonic  flow;  mesh  generation. 

В  расчете  трехмерных  течений  газа  важной  проблемой  является  уменьшение  размера  (количества  элементов)  расчетных  сеток,  что  позволяет  экономить  вычислительные  ресурсы  и  время  расчета.  Есть  течения,  в  которых  параметры  потока  меняются  вдоль  некоторого  направления  слабее,  чем  в  других  направлениях.  В  этом  случае  представляется  возможным  увеличивать  размер  ячеек  расчетной  сетки  вдоль  этого  направления,  тем  самым  уменьшая  количество  ячеек.  Этот  прием  используется,  например,  при  моделировании  пограничного  слоя,  в  котором  скорость  газа  резко  возрастает  с  увеличением  расстояния  до  обтекаемой  поверхности,  в  то  время  как  вдоль  поверхности  скорость  изменяется  значительно  слабее.  Другим  примером  практически  важного  случая  является  крыло  самолета.  Параметры  потока  меняются  вдоль  крыла  значительно  слабее,  чем  поперек,  поэтому  применение  элементарных  ячеек,  вытянутых  вдоль  размаха  крыла,  может  существенно  уменьшить  размер  расчетной  сетки  [1]. 

В  настоящей  работе  описан  алгоритм  построения  сеток  для  расчета  обтекания  крыла  с  шестигранными  ячейками  в  области  пограничного  слоя  и  пятигранными  ячейками  в  остальной  части  расчетной  области.  Размер  ячеек  может  меняться  вдоль  размаха  крыла  по  любому  заданному  закону,  например,  сетка  может  сгущаться  в  концевой  области.  Крыло  самолета,  как  правило,  имеет  крутку,  то  есть  локальный  угол  наклона  корды  крыла  меняется  вдоль  размаха.  Он  максимален  в  корневой  части  крыла  и  минимален  в  концевой  части.

За  основу  при  построении  трехмерной  сетки  берется  двумерная  сетка  (структурированная  или  неструктурированная).  Пространственные  элементы  строятся  экструдированием  (продавливанием)  двумерной  сетки  в  направлении  вдоль  размаха  крыла  с  поворотом  на  малый  угол,  соответствующий  крутке  крыла  области  расчетной  сетки,  примыкающей  к  крылу.  Таким  образом,  сетка  конструируется  на  основе  параллельного  переноса  исходной  двумерной  сетки  с  одновременной  ее  деформацией.  Область  сетки  радиуса  r₁,  содержащая  крыловой  профиль,  поворачивается  на  некоторый  угол  Δφ  вокруг  начала  координат,  находящегося  внутри  профиля,  область  сетки,  находящаяся  за  пределами  окружности  r  >  r₂  не  деформируются,  а  узлы  сетки,  попадающие  в  кольцо  r₁<  r  <  r₂,  поворачиваются  на  угол  (r₂  –  r)Δφ/(r₂  –  r₁).

Программа,  реализующая  описанный  алгоритм,  написана  на  языке  Паскаль.  Исходные  двумерные  сетки  построены  с  помощью  свободно  распространяемого  пакета  Gmsh  [4],  позволяющего  сохранять  построенную  сетку  в  большом  количестве  форматов.  В  качестве  входного  был  выбран  формат  SU2  [3].  На  выходе  трехмерная  расчетная  сетка  записывается  в  формате  TGrid  [6],  используемом  в  пакете  ANSYS  [2].

В  качестве  примера  ниже  приводится  результаты  расчета  трансзвукового  трехмерного  обтекания  сегмента  крыла  J78  [5].  Методом  конечных  объемов  решались  уравнения  Навье-Стокса,  осредненные  по  Рейнольдсу.  Принята  модель  турбулентности  k-ω  SST.  Расчеты  проводились  с  помощью  пакета  ANSYS  CFX  [2].  Исходная  двумерная  гибридная  расчетная  сетка,  имеющая  линзообразную  форму,  представлена  на  рис.  1.

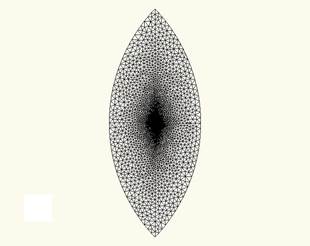
Рисунок  1.  Исходная  двумерная  расчетная  сетка,  содержащая  33664  элемента.  Слева  —  общий  вид,  справа  —  фрагмент  сетки  вблизи  носика  профиля

Расчетная  область  ограничена  двумя  дугами  окружности,  на  одной  из  дуг  задаются  входные  граничные  условия  (число  Маха,  направление  скорости  набегающего  потока,  температура  потока),  на  другой  —  среднее  давление.  Температура  и  давление  соответствуют  параметрам  стандартной  атмосферы  на  высоте  10  км.  Размеры  расчетной  области  по  горизонтали  80  хорд  профиля,  по  вертикали  —  200  хорд.  Двумерные  расчеты  обтекания  профиля  J78  дают,  что  при  фиксированном  числе  Маха  М  =  0,84  увеличение  угла  атаки  приводит  к  перестройке  конфигурации  сверхзвуковых  зон,  примыкающих  к  верхней  поверхности  профиля  при  некотором  значении  a  =  –  0.82^o.  Две  сверхзвуковые  зоны  сливаются  в  одну,  при  этом  скачком  увеличивается  подъемная  сила.  Обратный  процесс  (уменьшение  угла  атаки)  сопровождается  расщеплением  упомянутой  сверхзвуковой  зоны  на  две  и  скачкообразным  уменьшением  подъемной  силы  при  a  =  –  0.84^o. 

На  рис.  2  приведен  результат  расчета  трансзвукового  обтекания  сегмента  крыла  с  круткой,  концы  которого  имеют  углы  атаки  a₁  =  –  2,21^о  и  a₂  =  –    0,49^о.  Длина  сегмента  крыла  равна  4  хордам.  Таким  образом,  расчетный  объем  представляет  собой  цилиндр  с  линзообразным  основанием.  На  торцах  цилиндра  накладывается  условие  симметрии.  Граничное  значение  угла  атаки,  при  котором  происходит  слияние  или  расщепление  сверхзвуковых  зон,  примыкающих  к  верхней  поверхности  в  плоской  задаче  обтекания  профиля  находится  внутри  диапазона  (a_1,  a₂)  Однако  расчет  дает  две  сверхзвуковые  зоны  на  всем  протяжении  сегмента.  Форма  сверхзвуковых  зон  и  расстояние  между  ними  зависят  от  локального  угла  атаки. 

Рисунок  2.  Конфигурация  сверхзвуковых  зон,  примыкающих  к  крыловому  сегменту

В  указанном  примере  число  слоев  расчетной  сетки  вдоль  крыла  равно  20,  а  общее  число  элементов  сетки  составляет  673280  элементов.  Увеличение  числа  слоев  в  два  раза  не  меняет  формы  и  расположения  сверхзвуковых  зон,  аэродинамические  коэффициенты  изменяются  незначительно.

Таким  образом,  предлагаемый  алгоритм  позволяет  строить  сетки  для  расчета  трансзвукового  обтекания  крыльев  с  круткой,  имеющие  вытянутые  вдоль  крыла  ячейки.  Такие  сетки  имеют  относительно  небольшой  размер  и  вместе  с  тем  позволяют  прогнозировать  трехмерные  эффекты  обтекания. 

Список  литературы:

1.Богатырев  В.В.  Алгоритм  построения  экструзивных  объемных  сеток  около  крыла  самолета  //  Ученые  записки  ЦАГИ.  —  2012.  —  Т.  43.  —  №  1.  —  С.  71—79.

2.ANSYS  CFX-Solver  Modeling  Guide.  Release  13.0.  Canonsburg:  ANSYS,  Inc.,  2010.  —  604  p.

3.Copellan  S.  Users  Guide  SU2.  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  http://adl-public.stanford.edu/docs/display/SUSQUARED/User%27s+Guide   (дата  обращения:  10.08.14).

4.Geuzaine  Ch.,  Remacle  J.-F.  Gmsh  Reference  Manual  2014  —  278  p.  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  http://geuz.org/gmsh/doc/texinfo/gmsh.pdf  (дата  обращения:  10.08.14).

5.Kuzmin  A.  Non-unique  transonic  flows  over  airfoils  //  Computers  and  Fluids.  —  2012.  —  Vol.  63.  —  P.  1—8.

6.TGrid  5.0  User's  Guide.  ANSYS,  Inc.  2008.  —  281  p.  [Электронный  ресурс].  — (дата  обращения:  10.08.14).