ПРИМЕНЕНИЕ  СИСТЕМЫ  КОМПЬЮТЕРНОЙ  МАТЕМАТИКИ  MAPLE  ДЛЯ  РЕШЕНИЯ  ЗАДАЧ  ДИФФЕРЕНЦИАЛЬНОЙ  ГЕОМЕТРИИ

Голанова  Анна  Викторовна

канд.  пед.  наук,  доцент  кафедры  информатики  и  вычислительной  математики  Ленинградского  государственного  университета  имени  А.С.  Пушкина,  РФ,  г.  Пушкин

E -mail:  golanova@yandex.ru

Голикова  Екатерина  Ивановна

канд.  пед.  наук,  доцент  кафедры  информатики  и  вычислительной  математики  Ленинградского  государственного  университета  имени  А.  С.  Пушкина,  РФ,  г.  Пушкин

E -mail:  golikova_kat@inbox.ru

THE  SYSTEM  OF  COMPUTER  MATHEMATICS  MAPLE  TO  SOLVE  PROBLEMS  OF  DIFFERENTIAL  GEOMETRY

Anna  Golanova

candidate  of  Science,  associate  professor  of   department  of  computer  science  and  calculus  mathematics  of  Pushkin  Leningrad  State  University,  Russia,  Pushkin

Ekaterina  Golikova

candidate  of  Science,  associate  professor  of   department  of  computer  science  and  calculus  mathematics  of  Pushkin  Leningrad  State  University,  Russia,  Pushkin

АННОТАЦИЯ

В  статье  представлен  алгоритм  решения  геометрических  задач,  приводящих  к  дифференциальным  уравнениям  первого  порядка,  и  рассмотрена  его  реализация  в  системе  Maple.

ABSTRACT

The  article  presents  an  algorithm  for  solving  geometric  problems  leading  to  differential  equations  of  the  first  order,  and  its  realization  in  Maple  system.

Ключевые  слова:  компьютерное  моделирование;  дифференциальное  уравнение,  геометрическая  задача

Keywords:  computer  simulation;  differential  equation,  geometric  problem.

В  компьютерном  моделировании  дифференциальные  уравнения  занимают  особое  место.  Математическое  исследование  какого-либо  реального  явления  или  процесса  часто  приводит  к  решению  таких  уравнений,  поскольку  сами  законы,  которым  подчиняется  то  или  иное  явление  или  процесс,  записывают  в  виде  дифференциальных  уравнений.

В  курсе  «Компьютерное  моделирование»  для  бакалавров  по  направлению  050100.62  «Педагогическое  образование»  рассматриваются  геометрические  задачи,  приводящие  к  решению  дифференциальных  уравнений  первого  порядка  [1].

Выделим  основные  типы  таких  задач  (по  [2,  с.  158—161]):

1.  задачи,  приводящие  к  решению  уравнений  с  разделяющимися  переменными  (например,  найти  кривые,  у  которых  точка  пересечения  любой  касательной  с  осью  абсцисс  имеет  абсциссу,  вдвое  меньшую  абсциссы  точки  касания);

2.  задачи,  приводящие  к  решению  однородных  уравнений  (например,  найти  кривые,  у  которых  поднормаль  равна  разности  между  модулем  радиус-вектора  кривой  и  абсциссой  точки  касания);

3.  задачи,  приводящие  к  решению  линейных  уравнений  (например,  найти  кривые,  у  которых  площадь  трапеции,  ограниченной  осями  координат,  касательной  и  ординатой  точки  касания,  есть  величина  постоянная,  равная  3a²);

4.  задачи,  приводящие  к  решению  уравнений,  не  разрешённых  относительно  производной  (например,  найти  кривую,  проходящую  через  начало  координат  и  такую,  что  отрезок  нормали  к  ней,  отсекаемый  сторонами  первого  координатного  угла,  имеет  постоянную  длину,  равную  2);

5.  задачи,  приводящие  к  уравнениям,  допускающим  понижение  порядка  (например,  найти  кривые,  у  которых  радиус  кривизны  обратно  пропорционален  косинуса  угла  между  касательной  и  осью  абсцисс).

Рассмотрим  алгоритм  решения  геометрических  задач,  приводящих  к  дифференциальным  уравнениям  первого  порядка:

1.  построить  чертёж  в  декартовых  или  полярных  координатах;

2.  обозначить  искомую  кривую  через  y  =  y(x)  (если  задача  решается  в  прямоугольных  координатах)  и  выразить  все  упоминаемые  в  задаче  величины  через  три  величины:  x,  y,  y';

3.  воспользоваться  данным  в  условии  задачи  соотношением,  которое  позволяет  получить  дифференциальное  уравнение;

4.  решить  полученное  уравнение  и  найти  искомую  функцию  y(x).

Для  составления  дифференциального  уравнения  необходимо  знать  некоторые  простейшие  результаты  по  теории  плоских  кривых  из  дифференциальной  геометрии,  а  именно: 

1.  способы  задания  кривых:  в  декартовых  координатах,  в  параметрическом  виде,  в  полярных  координатах;

2.  положительное  направление  кривой;

3.  уравнение  касательной,  уравнение  нормали,  положительное  направление  касательной,  положительное  направление  нормали;

4.  подкасательная  кривой,  поднормаль  кривой;

5.  длина  дуги  кривой;

6.  радиус  кривизны  кривой,  радиус-вектор.

Для  решения  полученного  дифференциального  уравнения  можно  использовать  системы  компьютерной  математики  (например,  Mathcad,  Maple)  и  онлайн  калькуляторы.

В  качестве  примера  приведём  решение  следующей  геометрической  задачи:  найдите  уравнение  кривой,  проходящей  через  точку  (1,2)  и  обладающей  тем  свойством,  что  отношение  ординаты  любой  её  точки  к  абсциссе  пропорционально  угловому  коэффициенту  касательной  к  этой  кривой,  проведенной  в  той  же  точке,  с  коэффициентом  пропорциональности  k  =  3  [1,  c.  114,  №  368].

При  решении  задачи  будем  использовать  описанный  выше  алгоритм.

1.  Построим  чертёж  к  задаче  в  декартовых  координатах  (см.  Рис.  1).

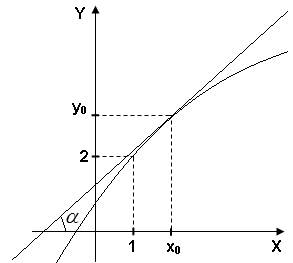
Рисунок  1.  Иллюстрация  задачи

2.  Обозначим  искомую  кривую  через  y  =  y(x).

3.  Составим  дифференциальное  уравнение,  воспользовавшись  условием  задачи.

Отношение  ординаты  любой  точки  к  абсциссе  пропорционально  коэффициенту  касательной  к  этой  кривой,  проведенной  в  той  же  точке,  т.  е.  .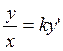

Коэффициент  пропорциональности  равен  3,  отсюда:  .

Так  как  кривая  проходит  через  точку  (1,2),  то  начальное  условие  задачи  Коши:  y(1)  =  2.

4.  Найдём  аналитическое  решение  получившегося  дифференциального  уравнения  в  системе  Maple.

Подключим  пакет  DETools  для  решения  дифференциального  уравнения  и  зададим  само  уравнение:

with(DETools):  d  :=  y(x)/x  =  3*(diff(y(x),  x)):

Воспользуемся  функцией  dsolve  для  нахождения  общего  решения:

dsolve(d,  y(x));

В  результате  получим:

y(x)  =  _C1  x^1/3;

Найдём  частное  решение  дифференциального  уравнения,  воспользовавшись  начальным  условием  y(1)  =  2.

dsolve({d,  y(1)  =  2},  y(x));

В  результате  получим:

y(x)  =  2  x^1/3;

Таким  образом,  уравнение  искомой  кривой  имеет  вид:  .

Отметим,  что  система  Maple  позволяет  решить  дифференциальное  уравнение  не  только  аналитически,  но  и  численно.  Для  этого  воспользуемся  функцией  dsolve,  но  с  дополнительными  параметрами,  например:

dsol:=dsolve(d1,  type  =  numeric,  method  =  classical[foreuler],  output  =  array([1,  1.1,  1.2,  1.3,  1.4,  1.5,  1.6,  1.7,  1.8,  1.9,  2])), 

где  d1  –  задача  Коши,  type  –  параметр,  указывающий  на  то,  что  решение  будет  численным,  method  –  выбранный  численный  метод  решения,  output  –  массив  выводимых  значений.

В  Maple  реализованы  следующие  численные  методы  решения  дифференциальных  уравнений:  метод  Рунге-Кутта-Фельберга  4—5-ого  порядка  (rkf45);  классический  метод  Рунге-Кута  4-ого  порядка  (classical[rk4]);  прямой  метод  Эйлера  (classical[foreuler]);  усовершенствованный  метод  Эйлера  (classical[heunform]);  модифицированный  метод  Эйлера  (classical[impoly]);  метод  Рунге-Кутта  7—8  порядка  (dverk78);  одношаговый  (gear)  и  многошаговый  методы  Гира  (mgear).

Существует  возможность  построения  графиков  аналитического  и  численного  решений. 

Для  построения  графика  аналитического  решения  воспользуемся  функцией  plot  из  пакета  plots,  например:

plot(2*x^(1/3),  x  =  1  ..  2,  style  =  point,  color  =  yellow),

где:  2*x^(1/3)  —  найденное  аналитическое  решение, 

x  —  интервал  построения, 

style  —  стиль  графика, 

color  —  цвет  графика.

Для  построения  графика  численного  решения  воспользуемся  функцией  odeplot  из  пакета  DETools,  например:

odeplot(dsol,  [x,  y(x),  color  =  red,  style  =  POINT],  1  ..  2),

где:  dsol  –  найденное  численное  решение,  x,  y(x),  color, 

style  —  параметры  графика, 

1..2  —  интервал  построения.

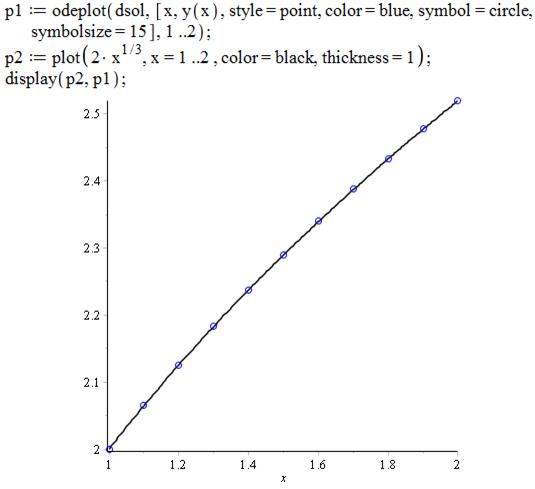
Рисунок  2.  Графики  аналитического  и  численного  решений  дифференциального  уравнения

Таким  образом,  использование  системы  Maple  при  решении  данной  геометрической  задачи  позволяет  не  только  найти  аналитическое  и  численное  решение,  но  и  визуализировать  его.  Возможность  построения  графиков  аналитического  и  численного  решения  в  одной  плоскости  даёт  возможность  оценить  ошибку  найденного  численного  решения.

Список  литературы

1.Высшая  математика:  Методические  указания  и  контрольные  задания  для  студентов-заочников  инженерно-технических  специальностей  высших  учебных  заведений  /  Арутюнов  Ю.С.,  Полозков  А.П.,  Полозков  Д.П.;  Под  ред.  Ю.С.  Арутюнова.  М.:  Высш.  школа,  1983.  —  128  с.

2.Голанова  А.В.,  Голикова  Е.И.  К  вопросу  об  отборе  содержания  лабораторных  работ  по  дисциплине  «Компьютерное  моделирование»  для  бакалавров  по  направлению  «Педагогическое  образование».  //  XVIII  Царскосельские  чтения:  материалы  междунар.  науч.  конф.  СПб:  ЛГУ  им.  А.С.  Пушкина,  —  2014.  —  Т.  III.  —  С.  130—134.

3.Зайцев  В.Ф.,  Петрушенко  А.А.,  Швецкий  М.В.  Дифференциальные  уравнения  (структурная  теория).  Практикум.  Часть  1.  Учебное  пособие  для  студентов  математического  факультета.  СПб.:  Интерлайн,  2008.  —  596  с.