ЭФФЕКТ  МАКСИМАЛЬНОГО  НАГРЕВАНИЯ  В  ПРОЦЕССЕ  ДИФФЕРЕНЦИРОВАННОЙ  ПЕРЕДАЧИ  ТЕПЛОТЫ

Зураб  Габриелович  Ростомашвили

д-р  физ.-мат.  наук,  профессор  департамента  информатики,  математики  и  физики  Телавского  Государственного  Университета  им.  Я.  Гогебашвили,  Грузия,  г.  Телави

E-mail: 

THE  EFFECT  OF  MAXIMAL  HEATING  IN  THE  PROCESS  OF  DIFFERENTIATED  HEAT  TRANSFER

Zurab  Rostomashvili

doctor  of  Science  ,professor  of  department  information,  mathematics  and  physics  of  Telavi  J.  Gogebashvili  state  university,  Georgia,  Telavi

АННОТАЦИЯ

Интересна  задача  о  максимальной  передаче  теплоты.  Газы,  жидкости  и  твердые  порошки  можно  разделить  на  большое  число  подсистем  и  к  ним  можно  применить  метод  дифференцированной  передачи  теплоты,  при  котором  в  тепловом  контакте  участвуют  холодное  тело  полностью  и  маленькая  часть  горячего  тела.  Получены  значения  максимальных  температур  для  классических  и  квантовых  систем.  Показано,  что  температура  холодной  системы  увеличивается  более,  чем  при  непосредственном  обычном  тепловом  контакте  для  классических  и  квантовых  систем.

ABSTRACT

Task  of  maximal  heat  transfer  is  very  important.  Gases,  liquids  and  solid  powders  can  be  divided  into  many  different  subsystems.  For  Such  systems  are  available  to  use  differentiated  method  of  heat  transfer.  In  this  case  a  cold  body  totally  and  a  small  part  of  hot  body  (almost  infinitely  small)  are  involved  in  thermal  process.  The  values  of  maximal  temperature  are  obtained  for  both  classic  and  quantum  systems.  It  is  shown  that  temperature  for  cold  system  incises  rather  than  for  direct  thermal  contact.

Ключевые  слова:  дифференцированная  передача  теплоты;  непосредственный  тепловой  контакт;  температура.

Keywords:  differentiated  transfer  of  heat;  Differential  heat  transfer;  transfer  of  Thermal  energy  by  direct  contact;  temperature. 

Работа  и  теплота  являются  одними  из  самых  важных  понятий  термодинамики.  При  циклических  обратимых  (цикл  Карно)  процессах  тепловые  двигатели  совершают  максимальную  работу  [1].  Само  собой  представляет  интерес  задача  о  максимальной  передаче  теплоты.  При  непосредственном  тепловом  контакте  между  горячим  и  холодним  телом  о  максимуме  и  нельзя  говорить,  однако  для  газов,  жидкостей  и  твердых  порошков  возможен  отличный  от  обычного,  процесс  теплопередачи  [2,  3],  т.  н.  дифференцированная  передача  теплоты  (ДПТ).  Суть  этого  процесса  заключается  в  том,  что  в  тепловом  контакте  участвуют  холодное  тело  полностью  и  маленкая  часть  (в  пределе  бесконечно  маленкая)  горячего  тела.  Т.  е.  горячее  тело  можно  разделить  на  оченъ  большое  число  частей,  что  не  представляет  трудность  для  вышеупомянутых  структур.  Горячее  тело    разделяется  на  большое  (в  дальнейшем  на  бесконечно  большое)  число  подсистем.  Подсистемы  при  этом  бесконечно  малы  по  отношению  горячего  тела,  хотя  они  должны  содержать  бесконечно  большое  число  частиц  (в  противном  случае  для  них  понятие  температуры  потеряло  смысл).  При  ДПТ  с  холодним  телом  сначала  приводят  в  тепловой  контакт  первую  подсистему  горячего  тела.  После  наступления  теплового  равновесия  эта  подсистема  удаляется  от  холодного  тела  и  больше  не  соприкасается  как  с  горячим,  так  и  с  холодным  телом.  Такую  процедуру  повторяют  для  второй,  третьей  и  т.  д.  последней  подсистемы.  В  конечном  итоге,  подсистемы  которые  уже  были  в  тепловом  равновесии  с  постепенно  опять  собираются  в  одну  систему,  которая  уже  охложденна.

Для  решения  задачи  максимального  нагревания  в  процессе  передачи  теплоты  в  классическом  случае,  напишем  уравнение  теплового  баланса  между  системы  ,  и  -ой  подсистемы  тела  .  Удельные  теплоёмкости  соответственно  обозначим  через    и  ,  массы  через    и  .  Начальную  температуру  тела    через  ,  а  температуру  тела    перед  тепловым  контактом  -ой  подсистемы  тела  ,  через  ,  массу  -ой  подсистемы  тела    через  .  После  теплового  равновесия  температура  тела    получает  приращение  ,  т.к.  .  Уравнение  теплового  баланса  имеет  вид:

  .  (1)

Т.  к.  ,  ,    и    величины  одного  порядка,  в  уравнении  (1)  можем  опустить  член  ,  после  чего  уравнение  (1)  принимает  вид: 

  .  (2)

На  основе  вышесказанного,  исходя  из  того,  что  мы  рассматриваем  очень  большое  число  подсистем,  ,  в  уравнении  (2)  можем  заменить  ,  .  В  этом  случае  (2)  принимает  вид: 

.  (3)

  и    в  интервале    будем  считать  очень  слабо  зависящимы  от  температуры.  За  начальное  условие  уравнения  (3)  можем  принять  ,  т.  е.  температура  тела    была    пока  подсистемы  тела    не  начали  тепловой  контакт  с  .

Интегрируя  (3),  для  конечной  температуры    получаем:

  ,  (4)  где  .

Рассмотрим  случай  когда  тело    не  разделяется  на  подсистемы  и  непосредственно  приходит  в  тепловом  равновесии  с  .  Если  конечную  температуру  обозначим  через  ,  уравнение  теплового  баланса  принимает  вид: 

,  (5)

и  для  окончательной  температуры  тела    получаем:

,  (6) 

В  случае  когда  ,  в  (4)  можем  заменить:  ,  после  чего  (4)  принимает  вид:

,

что  совпадает  значением  (6)  для  непосредственного  теплового  контакта  (НТК).  Эта  ситуация  для  ДПТ  соответствует  тому  случаю,  когда  тело    оченъ  маленькое,  и  представляет  одну  из  вышерассмотренных  подсистем!

В  случае  когда  ,  (4)  принимает  вид:  ,  эта  ситуация  для  ДПТ  соответствует  тому  случаю,  когда  тело    оченъ  маленькое.  Т.к.  ,  такой  же  результат  получаем  из  (6)  для  непосредственного  теплового  контакта:

.

Таким  образом  когда  одно  из  тел  участвующих  в  процессе  теплообмена  оченъ  маленькое,  как  ДПТ  так  и  НТК  дают  одинаковые  результаты.  Однако  в  реальных  ситуациях    порядка  единицы  и  к  примеру,  когда  ,  процесс  ДПТ  даёт  для  окончательной  температуры  ,  в  то  время  когда  процесс  НТК  даёт  значение  .  В  итоге  можем  утверждать,  что  для  классических,  неквантовых  систем  в  реальных  ситуациях  ДПТ  даёт  эффект  максимального  нагревания  в  процессе  передачи  теплоты.

Рассмотрим  ДПТ  для  спиновых  квантовых  систем.  В  отличии  от  классичесских  такие  системы  характеризуются  как  положительными,  так  и  отрицательными  абсолютными  температурами.  Обозначим  для  и    слабовзаимодействующих  спиновых  систем  число  спиновых  частиц  через    и  ,  температуры    и    соответственно.  Вдоль  направления  магнитного  поля  проекция  спина    принимает    значения  ()  и  соответственно  получаем    равноудалённых  невырождённых  энергетических  уровней  с  энергией  ,  где    и    представляют  магнитный  момент  спина  и  индукцию  магнитного  поля  соответственно.  Если  ввести  обратную  температуру  ,  для  статистической  суммы  такой  системы  получаем:

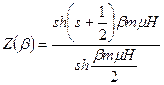  .  (7)

Для  энергии,  которая  ,  приходится  на  одну  частицу  в  случае    ,  имеем  [2—4]:

,  (8)

На  основе  (8)  для  энергии  спиновых  систем    и    напишем:

,  .

Т.  к.  при  НТК  между  спиновыми  системами    и  число  частиц  полученной  системы  равно  ,  поэтому  для  обратной  равновесной  температуры  системы    получаем:

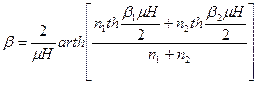  ,  (9)

Формула  (9)  уже  даёт  возможность  рассмотра  ДПТ  между  спиновими  системами    и    [1,  2].  Т.  к.  обе  системы  макроскопичны,  ,  поэтому  число  частиц  тела    -,  которая  приходит  в  тепловом  равновесии  с  телом  не  может  быть  меньше  единицы  и  при  этом  должна  быть  бесконечно  маленьким  по  отношению  с  .  В  таком  случае  на  основе  (9)  при  ДПТ  получим:

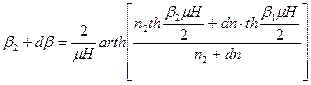  (10)

Разлагая  (10)  в  ряд  по  ,  в  линейном  приближении  получим:

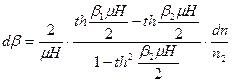.  (11)

Т.  к.  ,  поэтому    как  для  положительных,  так  и  для  отрицательных  абсолютных  температур  и  числитель  выражения  (11)  отрицателен.  А  из  условия 

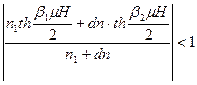
получаем,  что  знаменатель  выражения  (11)  положителен.  Всё  это  приводит  к  тому  ,что  температура  системы    повышается.  Т.  к.  при  ДПТ    меняется  от  0  до  ,  тогда  на  основе  (11)  в  конце  процесса  для  обратной  температуры,  которая,  соответствует  максимальной  абсолютной  температуре,  получим:

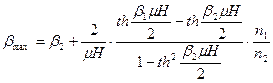  (12)

На  основе  численных  вычислений  легко  показать,  что  при  ДПТ  система    нагревается  больше  чем  при  НТК.

Таким  образом  ,при  ДПТ  холодные  системы  нагреваются  сильнее,  чем  при  НТК  как  для  классических,  так  и  для  квантовых  систем.  При  ДПТ  холодное  тело  в  итоге  оказывается  более  нагретым  по  сравнению  с  горячим  телом.

Список  литературы:

1.Ландау  Л.Л.,  Лифшиц  Е.М.  Статистическая  физика.  Часть  1.  М.  Наука,  1976.  —  75  с.

2.Ростомашвили  З.  Дифференцированная  передача  теплоты  для  слабовзаимодействующих  спиновых  систем.  Труды  Телавского  Государственного  Университета  №  2.  (22),  Телави.  2007.  —  235—238  с. 

3.Угулава  А.,  Ростомашвили  З..  Дифференцированная  передача  теплоты.  Труды  Телавского  Государственного  Университета  №  2.,  Телави.  2005.  —  11—14  с.