БЕСКОНТАКТНАЯ  РАДИОТОМОГРАФИЯ  ЧЕРЕЗ  НЕПЛОСКУЮ  ГРАНИЦУ  РАЗДЕЛА  СРЕД  В  ПРИБЛИЖЕНИИ  ФАЗОВОГО  ЭКРАНА

Суханов  Дмитрий  Яковлевич

канд.  физ.-мат.  наук,  доцент  ТГУ,  РФ,  г.  Томск

E-mail: 

Завьялова  Ксения  Владимировна

аспирант,  НИ  ТГУ,  РФ,  г.  Томск

E-mail: 

VISUALIZATION  OF  VOLUME  DISTRIBUTED  SOUND  SOURCE  OBJECTS

Dmitry  Sukhanov

candidate  of  physics-mathematical  sciences ,  associate  professor  of  Tomsk  State  University,  Russia,  Tomsk

Kseniia  Zavialova

graduate  student  of  Tomsk  State  University,  Russia,  Tomsk

АННОТАЦИЯ

Предлагается  быстрый  метод  восстановления  трёхмерных  изображений  объектов  скрытых  под  неплоской  поверхностью  раздела  сред  на  основе  сверхширокополосных  (СШП)  локационных  измерений.  Предполагается,  что  радиолокатор  перемещается  в  плоскости  над  средой  и  производит  радиолокационные  СШП  измерения  с  фиксированным  шагом.  Решение  обратной  задачи  осуществлено  в  приближении  однократного  рассеяния  и  приближении  фазового  экрана  для  неплоской  поверхности.  Алгоритм  восстановления  радио  изображения  неоднородностей  в  среде  сводится  к  трёхмерному  быстрому  преобразованию  Фурье. 

ABSTRACT

A  fast  method  for  reconstructing  of  three-dimensional  images  of  hidden  objects  under  the  non-planar  surface  between  two  media,  which  is  based  on  ultra-wideband  (UWB)  radar  measurements.  It  is  assumed  that  the  radar  moves  in  the  plane  above  the  medium  and  produces  UWB  radar  measurements  in  fixed  steps.  The  inverse  problem  solved  in  single-scattering  approximation  and  the  approximation  of  the  phase  screen  for  a  non-planar  surface.  Radio  image  reconstruction  algorithm  of  heterogeneities  in  the  medium  is  reduced  to  a  three-dimensional  fast  Fourier  transform. 

Ключевые  слова:  радиотомография;  радиголография;  синтез  апертуры;  фокусировка;  радар  подповерхностного  зондирования.

Keywords:  radiotomography;  radioholography;  synthetic  aperture;  focusing;  ground  penetrating  radar.

В  подповерхностной  радиотомографии  существует  проблема  восстановления  радиоизобжраений  при  зондировании  через  неровную  границу  раздела  сред.  Большинство  существующих  методов  работают  в  приближении,  что  поверхность  земли  плоская  [6—7].  При  бесконтактном  зондировании  для  учёта  преломления  на  плоской  границе  используется  закон  преломления  Снеллиуса  [2].  Для  зондирования  множества  различных  реальных  сцен  такого  приближения  вполне  достаточно  [1].  Для  восстановления  изображений  могут  применяться  методы  на  основе  миграции  во  временной  области,  метод  Столта  [3]  и  другие  [8,  4].  Однако  если  неровность  поверхности  сравнима  с  центральной  длиной  волны  зондирующего  сигнала,  то  восстанавливаемые  изображения  существенно  искажаются.  То  есть  необходимо  учитывать  неровность  поверхности  при  решении  обратной  задачи.  Саму  форму  поверхности  можно  восстановить  при  бесконтактном  зондировании  существующими  методами  сверхширокополосной  радиотомографии  в  однородной  среде  [5].  Таким  образом,  форму  поверхности  можно  считать  известной. 

В  данной  работе  предлагается  метод  восстановления  трёхмерных  радиоизображений  неоднородностей  скрытых  в  однородной  среде  с  неровной  поверхностью  при  бесконтактном  радиозондировании,  когда  моностатический  радиолокатор  перемещается  в  горизонтальной  плоскости.  Предполагается,  что  форма  поверхности  известна  и  показатель  преломления  фоновой  среды  известен.

ПОСТАНОВКА  ЗАДАЧИ  И  РЕШЕНИЕ  ПРЯМОЙ  ЗАДАЧИ

Будем  рассматривать  схему  измерений  представленную  на  рис.  1.  Считаем,  что  излучающая  и  приёмная  антенны  находятся  настолько  близко,  что  расстоянием  между  ними  можно  пренебречь.  Излучатель  и  приёмник  перемещаются  в  горизонтальной  плоскости  на  высоте  h  над  верхней  границей  поверхности  раздела  сред.  Максимальный  разброс  поверхностной  неровности  обозначим  d.  Показатель  преломления  верхней  среды  обозначим  ,  а  показатель  преломления  нижней  среды  .  Будем  считать,  что  излучатель  излучает  сферические  волны.  Неровную  границу  раздела  сред  будем  описывать  в  приближении  фазового  экрана,  то  есть  будем  считать,  что  волны  при  прохождении  неровной  границы  распространяются  по  оси  z  и  приобретают  фазовый  набег  в  соответствии  с  данной  траекторией.  Далее  волна  распространяется  в  однородной  среде  с  показателем  преломления  .  После  падения  волны  на  рассеивающую  неоднородность  появляется  волна,  распространяющаяся  обратно  по  той  же  траектории,  в  приёмную  антенну. 

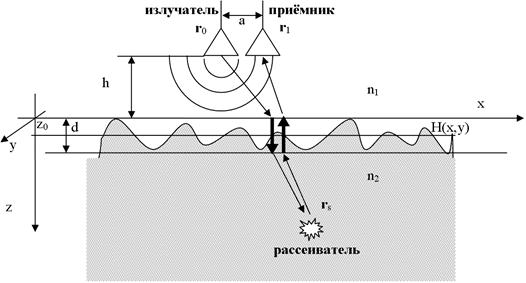
Рисунок  1.  Схема  измерений

По  измеренному  полю  в  приёмнике  необходимо  восстановить  изображение  неоднородностей  в  среде.  При  этом  учтём,  что  измеряется  только  интенсивность  поля.  За  счёт  интерференции  прямой  волны  (опорная  волна)  от  излучателя  в  приёмник  и  волны  рассеянной  неоднородностями  (предметная  волна)  возможно  извлечение  фазовой  информации. 

Запишем  решение  прямой  задачи  в  скалярном  приближении  однократного  рассеяния  и  фазового  экрана.  Поле  в  приёмной  антенне  можно  записать  в  виде:

,                                      (1)

где:  ,    —  поле,  прошедшее  фазовый  экран,

    —  поле  источника  на  высоте  , 

  —  функция  Грина, 

  ‑  функция  распределения  рассеивающих  неоднородностей, 

  —  волновое  число  в  верхней  среде, 

  —  волновое  число  в  нижней  среде, 

  —  волновое  число  в  свободном  пространстве, 

  —  координата  излучателя, 

  —  координата  точки  интегрирования  в  среде,  здесь  будем  считать  что  .

Согласно  (1)  было  проведено  численное  моделирование  моностатического  радиозондирования  объектов,  изображенных  на  рис.  2  для  неровной  границы  раздела  сред  изображенной  на  рис.  3.  Моделирование  проводилось  в  диапазоне  частот  от  1  до  10  ГГц  для  размера  апертуры  2  м,  ,  ,  =20  см.

Рисунок  2.  Изображение  моделируемых  объектов

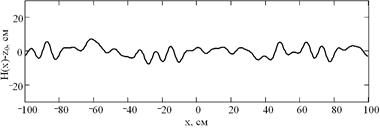
Рисунок  3.  Форма  моделируемой  неровной  поверхности

Результатом  моностатического  зондирования  будет  являться  поле  на  высоте  ,  то  есть  .  На  рис.  4  представлено  смоделированное  поле  в  области  измерений.

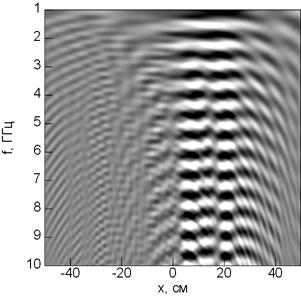
Рисунок  4.  Поле  в  области  измерений  на  различных  частотах,  действительная  часть

Под  влиянием  неровной  поверхности  произошло  искажение  поля,  что  должно  привести  к  искажениям  изображения  при  применении  методов,  в  которых  поверхность  считается  плоской. 

ВОССТАНОВЛЕНИЕ  РАСПРЕДЕЛЕНИЯ  НЕОДНОРОДНОСТЕЙ  ЗА  НЕРОВНОЙ  ПОВЕРХНОСТЬЮ  С  УЧЁТОМ  ЕЁ  ФОРМЫ

В  случае  если  искривлённая  поверхность  отклоняется  от  средней  горизонтальной  плоскости  на  расстояния  порядка  длины  волны,  то  её  невозможно  приближённо  считать  плоской.  Следовательно,  необходимо  разработать  метод  визуализации  радиотомографических  изображений  с  учётом  конкретной  формы  неровной  поверхности.

Решение  этой  обратной  задачи,  как  и  решение  прямой  задачи,  предполагается  осуществить  в  приближении  фазового  экрана.  То  есть  неровная  поверхность  будет  заменена  на  бесконечно  тонкий  фазовый  экран.  Так  же,  поскольку  рассматривается  случай  моностатического  зондирования  будем  рассматривать  рассеянные  радиоволны  как  поле  эквивалентных  источников  расположенных  в  точках  рассеивателей  и  излучающих  на  удвоенной  частоте.  То  есть,  обратная  задача,  сводится  к  задаче  обнаружения  множества  синфазных  источников  по  измерениям  поля  на  плоскости.  При  этом  надо  будет  учесть  прохождение  волн  через  неровную  границу  раздела  сред  в  приближении  фазового  экрана.  В  качестве  основы  для  решения  обратной  задачи  возьмём  метод,  описанный  в  статье  [5],  который  подобен  методу  миграции  Столта  [3],  применяемому  в  сейсмологии.

Сначала  необходимо  вычислить  поле  на  границе  раздела  сред  с  верхней  стороны  перед  прохождением  фазового  экрана.  Пусть  поле  в  области  измерений  задано  комплексной  функцией  ,  тогда  пространственный  спектр  поля  на  высоте  границы  раздела  сред    можно  записать  в  виде:

,

где  .

Теперь  необходимо  учесть  влияние  фазового  экрана.  Перейдём  в  пространство  координат: 

.

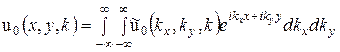Чтобы  компенсировать  искажение,  вносимое  фазовым  экраном  в  поле  необходимо  умножить    на  комплексно  сопряжённую  передаточную  функцию  фазового  экрана  то  есть:

Далее  опять  перейдем  в  область  пространственных  спектров  и  восстановим  пространственный  спектр  поля  в  нижней  среде  перед  прохождением  фазового  экрана: 

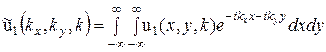
Теперь  изображение  неоднородностей  можно  восстановить  методом,  описанным  в  [5]:

,

где:    —  двумерный  пространственный  спектр  восстанавливаемого  изображения  на  глубине  .

Теперь  для  восстановления  трёхмерного  радиоизображения  достаточно  осуществить  преобразование  Фурье  по  пространственным  частотам  :

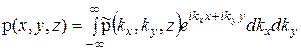.                         (3)

Таким  образом,  решение  обратной  задачи  с  учётом  прохождения  неровной  границы  раздела  сред  сводится  к  трехмерному  преобразованию  Фурье.

На  рис.  5  представлено  изображение  неоднородностей,  восстановленное  по  формуле  (3).  На  рис.  5  представлен  результат  восстановления  изображения  объектов,  скрытых  под  неровной  поверхностью.  Можно  видеть,  что  изображения  объектов  восстановлены  достаточно  отчётливо.  То  есть,  численная  модель,  показывает  возможность  применения  данного  метода. 

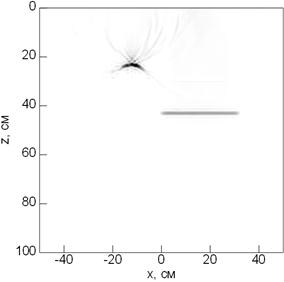
Рисунок  5.  Восстановленное  изображение  неоднородностей  (численное  моделирование)

Однако  стоит  учитывать,  что  и  прямая  и  обратная  задача  решались  в  одинаковых  приближениях:  приближении  фазового  экрана  и  с  заменой  рассеивателей  на  эквивалентные  источники  на  удвоенной  частоте.  То  есть,  по  сути,  обратная  задача  решалась  в  обратном  порядке  по  отношению  к  прямой  задаче,  и,  конечно,  показала  возможность  визуализации  рассеивающих  объектов.  Для  окончательной  проверки  применимости  предложенных  методов  решения  прямой  и  обратной  задач  моностатической  радиотомографии  через  неровную  границу  раздела  сред  необходимо  проведение  экспериментальных  исследований.

Заключение

В  работе  предложен  метод  восстановления  трёхмерных  радиоизображений  объектов  скрытых  в  однородной  среде  с  неровной  поверхностью.  Алгоритм  восстановления  сводится  к  быстрому  трёхмерному  преобразованию  Фурье  и  поэтому  может  быть  применён  в  системах  визуализации  реального  времени.  Для  учёта  неровности  поверхности  используется  приближение  фазового  экрана.  Результаты  численного  моделирования  показали  применимость  предложенного  метода. 

Список  литературы:

1.Capineri  L.,  Fiesoli  F.,  Windsor  C.,  “Holographic  radar:  A  strategy  for  uneven  surfaces”,  in  Proc.  14th  International  Conference  on  Ground  Penetrating  Radar  (GPR),  4-8  June,  2012,  Shanghai,  China,  —  pp.  143—145.

2.Fortuny-Guasch  J.,  "A  Novel  3-D  Subsurface  Radar  Imaging  Technique",  IEEE  Transactions  on  Geosciences  and  Remote  Sensing,  —  vol.  40,  —  №  2,  —  pp.  443—452,  February  2002. 

3.Stolt  R.H.,  “Migration  by  Fourier  transform”,  Geophysics,  —  vol.  43,  —  №  1,  —  pp.  23—48,  —  1978.

4.Sukhanov  D.Ya.,  Yakubov  V.P.,  “Application  of  linear  frequency  modulated  signals  in  three-dimensional  radio  tomography”,  Technical  physics,  —  vol.  55,  —  Issue  4,  —  pp.  546—550,  —  Apr  2010.

5.Sukhanov  D.Ya.,  Zav'yalova  K.V.,  “Reconstruction  of  3D  radio  images  from  multifrequency  holographic  measurements”,  Technical  physics,  vol.  57,  Issue  6,  —  pp.  819—823,  Jun  2012. 

6.Yakubov  V.P.,  Sukhanov  D.Ya.,  “Solution  of  a  subsurface  radio-imaging  inverse  problem  in  the  approximation  of  a  strongly  refractive  medium”,  Radiophysics  and  quantum  electronics,  vol.  50,  Issue  4,  —  pp.  299—307,  Apr  2007.

7.Yakubov  V.P.,  Omar  A.S.,  Suhanov  D.Y.,  et  al.  "New  Fast  SAR  Method  for  3-D  Subsurface  Radiotomography",  Tenth  International  Conference  on  Ground  Penetrating  Radar,  21—24  June,  2004,  Delft,  The  Netherlands,  —  pp.  103—106. 

8.Yilmaz  Oz.,  “Seismic  Data  Analysis:  processing,  inversion,  and  interpretation  of  seismic  data”,  2001.