МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  ЗАДАЧИ  РАЗРАБОТКИ  НЕФТЯНЫХ  МЕСТОРОЖДЕНИЙ

Григорян  Лусине  Арсеновна

старший  преподаватель  кафедры  высшей  алгебры  и  геометрии  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

E -mail:  honey.lusine@mail.ru

Тимофеева  Елена  Федоровна

канд.  физ.-мат.  наук,  доцент  кафедры  высшей  алгебры  и  геометрии  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

E-mail: 

MATHEMATICAL  MODELING  OF  THE  DEVELOPMENT  OF  OIL  FIELDS

Grigoryan  Lusine

senior  lecturer  of  Algebra  and  Geometry  department  Of  North  Caucasian  Federal  University,  Russia,  Stavropol

Timofeeva  Helena

candidate  of  Science,  assistant  professor  of  Algebra  and  Geometry  department

Of  North  Caucasian  Federal  University,  Russia,  Stavropol

АННОТАЦИЯ

В  статье  рассматривается  непоршневое  вытеснение  нефти  водой.  Построена  численная  модель  фильтрации  двухфазной  несжимаемой  жидкости.

ABSTRACT

The  problem  of  oil  production  by  means  of  non-piston  water  displacement  is  considered.  The  numerical  model  for  two−phase  incompressible  fluid  filtration  is  designed.

Ключевые  слова :  фильтрация;  несжимаемая  жидкость;  модель  Баклея-Леверетта.

Keywords :  filtration;  non-piston  water;  Bakly-Leveretta  model.

Введение.   В  настоящее  время  существенно  увеличились  масштабы  добычи  нефти  и  газа.  В  разработку  вводятся  новые  месторождения  со  сложными  физико-геологическими  условиями.  Решается  важнейшая  проблема  увеличения  полноты  извлечения  нефти  из  недр.  В  связи  с  этим  большое  значение  имеют  знание  современных  гидродинамических  методов  получения  информации  и  научных  основ  установления  оптимального  режима  эксплуатации  скважин  для  рационального  освоения  месторождений.  Определяющим  инструментом  для  обеспечения  этих  знаний  выступает  математическое  моделирование.

Добыча  нефти  в  большинстве  случаев  происходит  при  вытеснении  ее  в  поровом  пространстве  продуктивного  пласта  водой  или  газом.  Этот  процесс  применяется  при  естественных  режимах  эксплуатации  и  при  искусственных  методах  поддержания  пластового  давления  заводнением  или  нагнетанием  газа.  Теория  многофазной  многокомпонентной  фильтрации  служит  основой  для  расчета  таких  процессов  [6;  1—2)]  [4].

Одно  и  двухмерные  задачи  фильтрации  многофазной  жидкости  хорошо  изучены.  Для  них  построены  модели  и  схемы  расчета  [6].  С  учетом  активного  развития  вычислительной  техники  появились  особые  требования  к  алгоритмам  и  их  реализации.  Для  уменьшения  времени  решения  поставленных  задач  необходимо  применение  алгоритмов,  обеспечивающих  высокую  маштабируемость  и  возможность  эффективного  решения  на  многопроцессорных  вычислительных  системах.  Работа  посвящена  одному  из  подходов  численного  моделирования  процессов  фильтрации  двухфазной  несжимаемой  жидкости. 

Математическая  модель  двухфазной  фильтрации.

Рассмотрим  фильтрацию  двухфазной  жидкости,  состоящей  из  нефти  (н)  и  воды  (в),  в  пористой  среде  в  водонапорном  режиме.  Месторождение  покрыто  сетью  скважин  двух  типов:  водонагнетающих  и  продуктивных.  Схемы  их  расположения  могут  быть  различными.  Нефтеносный  пласт  считается  неограниченным,  постоянной  толщины,  пористая  среда  —  недеформируемой,  отношение  капиллярного  давления  к  полному  гидродинамическому  падению  давления  мало,  что  позволяет  рассмотреть  задачу,  подчиняющуюся  классической  модели  Бакли-Леверетта: 

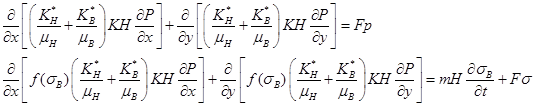
где:    —  водонасыщенность, 

  —  относительная  фазовая  проницаемость  для  нефти, 

  —  относительная  фазовая  проницаемость  для  воды, 

  —  давление, 

  —  проницаемость, 

  —  мощность  пласта, 

  —  функция  Баклея-Леверетта, 

  —  пористость  пласта, 

  —  вязкость  нефти, 

  —  вязкость  воды.  Необходимо  определить  функции  давления  ,  водонасыщенности  ,  которые  удовлетворяют  системе  (1).

Предположим,  имеется  тонкий  горизонтальный  нефтяной  пласт,  с  достаточно  большой  протяженностью.  Рассмотрим  математическую  модель  двухфазной  фильтрации  несмешиваемых  несжимаемых  жидкостей.  Введем  начальные  и  граничные  условия:

,                             

  ,                      

где:    —  граница  нефтеводоностного  пласта  с  «окружающей  средой»,

,     

где:    —  граница  скважины  с  нефтеводоносным  платом.

Аппроксимация  системы  уравнений

Аппроксимация  для  уравнения  давления

Аппроксимация  для  уравнения  водонасыщенности

где: 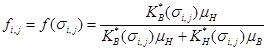   —  функция  Баклея-Леверетта,

  —  относительная  фазовая  проницаемость  для  нефти,

  —  относительная  фазовая  проницаемость  для  воды,

  , 

  , 

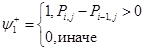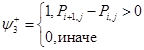
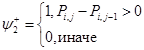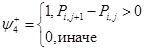
Пусть  расчетная  область    —  прямоугольная  область,  в  которой  будем  искать  решение  задачи.  В  области  введем  равномерную  пространственную  сетку  с  шагом  так,  чтобы  скважины  попадали  в  один  из  углов  сетки  и  неравномерную  временную  сетку.

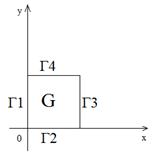
Рисунок  1.

Если  ,  тогда  .

Тогда  аппроксимация  уравнения  для  давления  имеет  вид:

Если  ,  тогда  .

Тогда  аппроксимация  уравнения  для  давления  имеет  вид:

Запишем  общий  вид  аппроксимации  системы  уравнений    с  учетом  граничного  условия  :

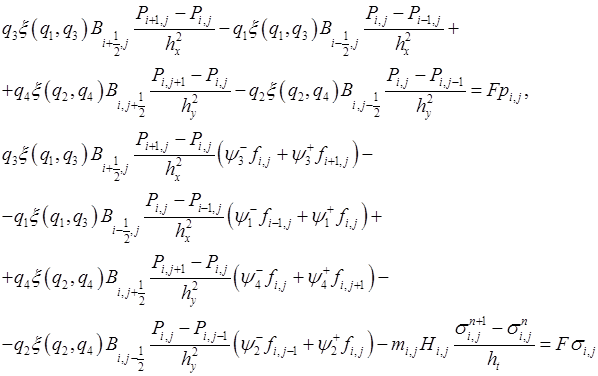
где:

,  ,

,  .

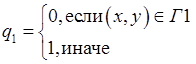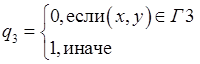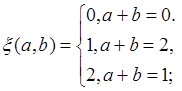
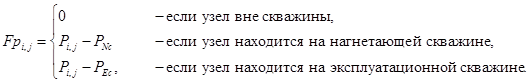
Имеем: 

  —  метры,    —  метры,    —  метры,    —  текущий  день,    —  прогнозируемый  период  (дни),    —  шаг  по  реальным  координатам  расчетной  области  (метры),    —  размер  реальной  расчетной  области  (метры). 

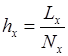  —  шаг  между  узами  сетки  (метры),  где    —  число  узлов  по  оси  .

  —  шаг  между  узами  сетки  (метры),  где    —  число  узлов  по  оси  .

  —  шаг  по  времени  (дни),  где    —  планируемое  количество  итераций  по  времени  для  системы  .

  Введем  следующие  обозначения

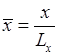  ,  ,  ,  где  .

Соответственно  новые  шаги  по  пространству  и  по  времени  будут

,    ,  .

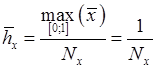Продифференцируем  с  учетом  новых  обозначений:

.

Заменим  частные  производные  системы  .  Обозначим 

.

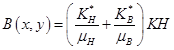Получим:

Коэффициент    будет  рассчитываться  также  по  формуле  ,  за  исключением  того,  что    будет  заменен  на  .

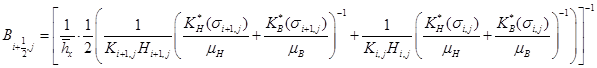
Продифференцируем  по  времени  второе  уравнение  системы 

, 

Получим

Запишем  аналог  системы    с  учетом  уравнений  ,  .  Получим

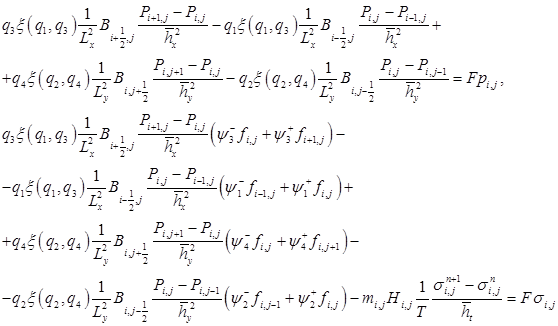
Схемы,  ориентированные  против  потока  членов  с  производными  первого  порядка  приводят  к  большему  повышению  устойчивости  метода  решения,  чем  для  схем,  включающих  центральные  разности  [3].  Система  явных  разностных  уравнений  позволяет  уменьшить  до  минимума  размазывание  фронта  скачка  водонасыщенности. 

  При  замене  системы  дифференциальных  уравнений  (1)  разностной  схемой  возникает  погрешность  аппроксимации.  Схема  имеет  второй  порядок  аппроксимации    для  временных  переменных  и    для  пространственных,  то  есть  оценка  погрешности  .

  При  задании  входных  данных,  в  процессе  реализации  задачи  появляются  ошибки,  связанные  с  округлением,  поэтому  одним  из  требований  к  разностной  схеме  является  устойчивость.  Численные  эксперименты,  выполненные  рядом  авторов,  позволили  сделать  вывод  о  том,  что  устойчивость  сохраняется,  если  шаг  в  системе  явных  разностных  уравнений  выбирать  из  условия 

Схема  решения  системы  уравнений:  на  каждом  временном  слое  определяется  водонасыщенность  при  фиксированном  давлении,  затем  находится  давление  на  текущем  слое  с  учетом  найденного  значения  водонасыщенности,  затем  осуществляется  переход  к  следующему  временному  шагу.  Для  сходимости  итераций  неявной  разностной  схемы  применяется  метод  верхней  релаксации  и  дальнейшее  распараллеливание  алгоритма.

Заключение

В  данной  работе  предложен  один  из  методов  решения  задачи  фильтрации  двухфазной  несжимаемой  жидкости.  Поставлена  математическая  задача  фильтрации  на  основе  классической  модели  Бакли-Леверетта,  составлены  разностные  схемы,  аппроксимирующих  систему  уравнений  (6).  Проделанная  работа  открывает  путь  к  дальнейшим  исследованиям.

Список  литературы:

1.Баренблатт  Г.И.,  Ентов  В.М.,  Рыжик  В.М.  Движение  жидкостей  и  газов  в  природных  пластах.  М.:  Недра,  1984.

2.Басниев  К.М.  Подземная  гидродинамика  /  К.М.  Басниев,  А.  М.  Власов,  И.Н.  Кочина.  М.:Наука,  1986. 

3.Григорян  Л.А.  Моделирование  фильтрации  двухфазной  жидкости  методом  конечных  элементов.  Вестник.  Северо-Кавказский  федеральный  университет.  Ставрополь:  СКФУ,  —  2013.  —  №  2.  —  С.  13—16.

4.Коновалов  А.Н.  Задачи  фильтрации  многофазной  несжимаемой  жидкости.  Новосибирск:  Наука,  1988.

5.Самарский  А.А.  Теория  разностных  схем.  М.:  Наука,  1989.

6.Aziz  К.,  Settari  A.  Petrolium  Reservoir  Simulation.  Calgary,  Alberta:  Blitzprint  Ltd.,  2002.