Статья опубликована в рамках: XVIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 мая 2014 г.)
Наука: Информационные технологии
Секция: Системный анализ, управление и обработка информации
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ НЕЙРОНОЙ СЕТИ, ИСПОЛЬЗУЕМОЙ В КАЧЕСТВЕ НАБЛЮДАТЕЛЯ В ОДНООСНОМ ГИРОСКОПИЧЕСКОМ СТАБИЛИЗАТОРЕ
Анисимов Ян Олегович
старший преподаватель кафедры Приборостроене Южно-Уральского Государственного Университета (НИУ), РФ, г. Челябинск
DETERMINE THE OPTIMUM PARAMETERS OF A NEURAL NETWORK USED AS AN OBSERVER IN UNIAXIAL GYRO STABILIZERS
Yan Anisimov
senior lector of South Ural State University(NRI), Russia Chelyabinsk
АННОТАЦИЯ
В работе рассматривается вопрос определения оптимальных параметров нейросетевого наблюдающего устройства гиростабилизатора. Рассмотрен вопрос устойчивости в зависимости от количества нейронов в скрытом слое, вида активационной функции и количества ячеек памяти на входе.
ABSTRACT
The paper deals with the issue of determining the optimal neural network estimator. The problem of stability depending on the number of neurons in the hidden layer activation function type and quantity of memory cells at the inlet.
Ключевые слова: нейронная сеть; наблюдающее устровйство.
Keywords : neural network; estimator.
В последнее время для целей управления все шире начинают применяться нейронные сети. Они показали свою эффективность для решения задач распознавания образов. Нейронные сети способны обучаться на основе соотношений «вход-выход», поэтому они могут обеспечить более простые решения для сложных задач управления.
При решении задач с применением нейронных сетей основным вопросом является вопрос о выборе структуры и параметров сети. От корректности выбора указанных элементов зависят не только количественные характеристики работы всей системы, но и принципиальная возможность выполнять нейронной сетью возложенные на неё задачи.
Ставится задача восстановления вектора состояния динамического объекта и формирование управления в цепи обратной связи. В качестве объекта выбран одноосный силовой гиростабилизатор, движение которого описывается в виде следующего векторно-матричного уравнения [1]:
|
|
(1) |
где: ![]() — кинетический момент гироблока,
— кинетический момент гироблока,
![]() — момент инерции гироплатформы,
— момент инерции гироплатформы,
![]() — момент инерции гироблока силового гиростабилизатора,
— момент инерции гироблока силового гиростабилизатора,
![]() — коэффициент демпфирования.
— коэффициент демпфирования.
Будем считать, что измерению доступен только угол прецессии гироскопа ![]() . Для компенсации внешнего возмущения
. Для компенсации внешнего возмущения ![]() , приложенного по оси стабилизации, будем подавать управление
, приложенного по оси стабилизации, будем подавать управление ![]() на двигатель стабилизации, который будет развивать момент, уравновешивающий внешнее возмущение. Для формирования управления
на двигатель стабилизации, который будет развивать момент, уравновешивающий внешнее возмущение. Для формирования управления ![]() необходимо знать весь вектор состояния
необходимо знать весь вектор состояния ![]() и иметь рассчитанный регулятор
и иметь рассчитанный регулятор ![]() . Так как нам доступна лишь одна компонента вектора состояния, то необходимо получить оценку всего вектора
. Так как нам доступна лишь одна компонента вектора состояния, то необходимо получить оценку всего вектора ![]() . В качестве устройства, выполняющее подобную оценку, будет выступать нейронная сеть [3].
. В качестве устройства, выполняющее подобную оценку, будет выступать нейронная сеть [3].
В ходе вычислительный экспериментов было выявлено, что решение задачи восстановления вектора состояния динамического объекта способна выполнять нейронная сеть со структурой типа «многослойный персептрон», на вход которого помимо текущего значения измеренной компоненты состояния подаются несколько предыдущих значений. Однако остается открытым вопрос об оптимальном выборе параметров нейронной сети. К этим параметрам можно отнести:
· количество слоев в многослойной сети;
· количество нейронов в каждом слое;
· вид активационной функции каждого нейрона.
Указанные параметры зависят от характера взаимосвязей «вход-выход», которые должны могут быть реализованы нейронной сетью. Известно [4] , что любые непрерывные функции могут быть аппроксимированы с заданной точностью при помощи нейросети, содержащей один скрытый слой нейронов с нелинейными функциями активации и выходной слой с линейными активационными функциями. Увеличение числа нейронов в скрытом слое и увеличение числа скрытых слоев повышают репрезентативные возможности нейронной сети. При этом вопрос о числе нейронов в скрытом слое и количестве запомненных состояний остается открытым. В общем виде задача выбора указных параметров не решена. Однако в работе [2] изложена методология синтеза многослойных нейронных сетей, как адаптивных систем определённого вида. В обычной практике построения нейронных сетей даются следующие рекомендации:
1. все выходные сигналы подаются всем нейронам;
2. вариант топологии определяется на основе априорных знаний о задаче.
В работе [5] приводится формула для определения необходимого количества весов в двухслойной нейронной сети:
|
|
(2) |
где: ![]() — общее количество весов в нейронной сети,
— общее количество весов в нейронной сети,
![]() — размерность входного вектора данных,
— размерность входного вектора данных,
![]() — размерность выходного вектора,
— размерность выходного вектора,
![]() — количество образцов для обучения.
— количество образцов для обучения.
В качестве исходных данных были выбраны данные переходного процесса, длительность которого составляет ![]() секунд, с шагом интегрирования 0,01 секунды. Таким образом, мы имеем 6284 отсчета по каждому из 3-х компонентов вектора состояния. Согласно оценке (2) общее количество весов в нейронной сети будет определяться неравенством:
секунд, с шагом интегрирования 0,01 секунды. Таким образом, мы имеем 6284 отсчета по каждому из 3-х компонентов вектора состояния. Согласно оценке (2) общее количество весов в нейронной сети будет определяться неравенством: ![]() . Т. к. данный диапазон значительный, то количество предыдущих запомненных состояний и количества нейронов в скрытом слое выбираются из диапазона от 1 до 10. Таким образом, общее количество весов в нейронной сети будет составлять
. Т. к. данный диапазон значительный, то количество предыдущих запомненных состояний и количества нейронов в скрытом слое выбираются из диапазона от 1 до 10. Таким образом, общее количество весов в нейронной сети будет составлять ![]() . В качестве критерия оптимальности выберем количество устойчивых переходных процессов в серии, состоящей из 10 опытов.
. В качестве критерия оптимальности выберем количество устойчивых переходных процессов в серии, состоящей из 10 опытов.
В качестве активационных функций были выбраны:
· сигмоидальная ;
· логистическая;
· линейная.
Рассмотрим таблицу количества устойчивых переходных процессов в серии экспериментов при сигмоидальной функции активации в скрытом нейроне (Таблица 1). Из таблицы видно, что 10 из 10 удачных экспериментов мы получим при глубине регрессии в 2 элемента и 1 нейроне в скрытом слое. Таким образом, общее число весов равно 6.
Рассмотрим теперь таблицу количества устойчивых переходных процессов в серии экспериментов при логистической функции активации в скрытом слое (Таблица 2). Максимальное количество удачных исходов равняется 9, что меньше, чем при сигмоидальной функции активации. Однако это количество было достигнуто при такой же структуре, как в случае с сигмоидальной функцией активации.
Таблица 1.
Количество удачных экспериментов при сигмоидальной функции активации
|
|
Кол-во нейронов в скрытом слое |
||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Кол-во элементов памяти |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
10 |
5 |
4 |
7 |
5 |
6 |
5 |
3 |
4 |
6 |
|
|
3 |
0 |
8 |
6 |
3 |
4 |
5 |
3 |
3 |
4 |
5 |
|
|
4 |
0 |
2 |
6 |
9 |
5 |
7 |
3 |
v |
5 |
4 |
|
|
5 |
0 |
5 |
6 |
5 |
7 |
3 |
8 |
6 |
4 |
3 |
|
|
6 |
0 |
7 |
3 |
4 |
4 |
2 |
2 |
2 |
5 |
2 |
|
|
7 |
0 |
5 |
3 |
4 |
4 |
2 |
1 |
5 |
6 |
2 |
|
|
8 |
0 |
0 |
4 |
3 |
2 |
0 |
3 |
0 |
5 |
3 |
|
|
9 |
0 |
1 |
2 |
2 |
0 |
4 |
4 |
0 |
3 |
2 |
|
|
10 |
0 |
1 |
2 |
1 |
2 |
1 |
1 |
2 |
0 |
2 |
|
Рассмотрим теперь таблицу количества устойчивых переходных процессов в серии экспериментов при линейной функции активации в скрытом слое (Таблица 3). Максимальное количество удачных исходов равняется 8 при 2 различных структурах сети: глубине регрессии в 3 элемента и 3 нейронах в скрытом слое; глубине регрессии в 2 элемента и 5 нейронах в скрытом слое. Первая структура будет являться более предпочтительной, так как в ней меньшее количество элементов.
Таблица 2.
Количество удачных экспериментов при логистической функции активации
|
|
Кол-во нейронов в скрытом слое |
||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Кол-во элементов памяти |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
9 |
6 |
5 |
7 |
6 |
6 |
7 |
6 |
2 |
7 |
|
|
3 |
0 |
8 |
8 |
8 |
8 |
6 |
5 |
5 |
4 |
5 |
|
|
4 |
0 |
5 |
6 |
6 |
6 |
3 |
4 |
7 |
4 |
7 |
|
|
5 |
0 |
2 |
7 |
3 |
4 |
7 |
3 |
6 |
5 |
7 |
|
|
6 |
0 |
6 |
6 |
6 |
3 |
6 |
6 |
7 |
4 |
6 |
|
|
7 |
0 |
6 |
6 |
4 |
4 |
1 |
2 |
6 |
3 |
6 |
|
|
8 |
0 |
3 |
4 |
1 |
2 |
2 |
3 |
4 |
5 |
5 |
|
|
9 |
0 |
1 |
0 |
3 |
5 |
4 |
2 |
4 |
3 |
3 |
|
|
10 |
0 |
1 |
0 |
1 |
3 |
4 |
2 |
3 |
1 |
5 |
|
Из проведенных экспериментов видно, что увеличение количества запомненных предыдущих состояний не всегда является благоприятным фактором для улучшения свойств нейронной сети, связанных с восстановлением переменных состояния. Более того, как показали опыты, оптимальным может считаться минимально возможное количество элементов памяти на входе при сигмоидальной и логистической функции активации. В вопросе об оптимальном количестве нейронов в скрытом слое прослеживается аналогичная тенденция. При этом стоит отметить, что количество устойчивых переходных процессов при большом значении нейронов в скрытом слое больше, чем в аналогичном случае для количества предыдущих запомненных состояний. Из этого можно сделать вывод о большей чувствительности нейронной сети к количеству элементов памяти.
Таблица 3.
Количество удачных экспериментов при линейной функции активации
|
|
Кол-во нейронов в скрытом слое |
||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Кол-во элементов памяти |
1 |
0 |
5 |
2 |
2 |
5 |
2 |
3 |
1 |
0 |
3 |
|
2 |
0 |
6 |
4 |
6 |
8 |
3 |
5 |
1 |
3 |
3 |
|
|
3 |
0 |
7 |
8 |
4 |
4 |
3 |
4 |
3 |
4 |
3 |
|
|
4 |
0 |
5 |
4 |
3 |
5 |
1 |
3 |
1 |
0 |
0 |
|
|
5 |
0 |
4 |
4 |
0 |
0 |
3 |
2 |
1 |
2 |
3 |
|
|
6 |
0 |
7 |
4 |
3 |
2 |
0 |
1 |
0 |
5 |
4 |
|
|
7 |
0 |
2 |
2 |
1 |
2 |
1 |
1 |
0 |
3 |
1 |
|
|
8 |
0 |
5 |
2 |
2 |
5 |
2 |
3 |
1 |
0 |
3 |
|
|
9 |
0 |
6 |
4 |
6 |
7 |
3 |
5 |
1 |
3 |
3 |
|
|
10 |
0 |
7 |
7 |
4 |
4 |
3 |
4 |
3 |
4 |
3 |
|
Из приведенных таблиц видно, что даже для линейной системы предпочтительным является наличие нелинейной активационной функции в составе нейронной сети. В данном случае мы получим большую вероятность получения удачного исхода. Очевидно, что для получения нейронной сети, способной выполнять возложенные на нее функции, при нелинейных функциях активации, достаточно малого количества весов в составе нейронной сети: от 6 до 30. При сигмоидальной и при логистической функции активации оптимальная структура сети будет иметь следующий вид: 2 элемента памяти, одно текущее состояние на входе и 1 скрытый нейрон.
Список литературы:
1.Кацай Д.А. Одноосный гиростабилизатор с наблюдателем Льюинбергера // Приборостроение: Темат. сб. науч. тр. 2002. — 76—80 с
2.Методы робастного, нейро-нечеткого и адаптивного управления / К.А. Пупков, Н.Д. Егупов, А.И. Гаврилов и др.; Под ред. К.А. Егупова. М.: Издательство МГТУ им. Н.Э. Баумана, 2002 — 744 с.
3.Справочник по теории автоматического управления / Под ред. А.А. Красовкого. М.: главная редакция физико-математической литературы, 1987. — 712 с.
4.Хайкин С. Нейронные сети. Полный курс. М.: Вильямс изд. 2006. — 1103 с.
5.Червяков Н.И., Рудакова Т.А. Определение оптимальной структуры нейронной сети динамической модели // Нейрокомпьютеры: разработка, применение. — 2008. — № 9 — 60—65 с.
дипломов


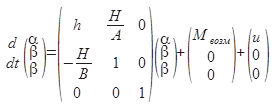
Оставить комментарий