ИНДУЦИРОВАННЫЙ  МАГНИТНЫЙ  МОМЕНТ  СИСТЕМЫ  МАГНИТНЫХ  ДИПОЛЕЙ

Шутый  Анатолий  Михайлович

д-р  физ.-мат.  наук,  вед.  науч.  сотр.  Ульяновского  государственного  университета,  РФ,  г.  Ульяновск

E-mail: 

INDUCED  MAGNETIC  MOMENT  OF  A  MAGNETIC  DIPOLE  SYSTEM

Shutyǐ  Anatoliy  Michailovich

dr.  math.  and  phys.,  senior  researcher,  Ulyanovsk  State  University,  Russia  Ulyanovsk

Работа  выполнена  при  поддержке  министерства  образования  и  науки  РФ.

АННОТАЦИЯ

На  основе  численного  анализа  исследованы  системы  трех  и  четырех  шарообразных  тел,  обладающих  дипольным  магнитным  моментом.  Показано,  что  при  исходном  состоянии  с  нулевым  суммарным  магнитным  моментов  под  воздействием  переменного  магнитного  поля  устанавливаются  различные  режимы  индуцированного  магнитного  момента,  в  том  числе  квазистатические  состоя­ния.  Выявлены  существенные  отличия  данных  режимов,  отвечающих  разным  системам.  Проведены  исследования  величины  и  направления  магнитного  момента  системы,  а  также  состояний  динамической  бистабильности. 

ABSTRACT

The  systems  of  three  and  four  spherical  bodies  with  the  dipole  magnetic  moment  have  been  investigated  using  a  numerical  analysis.  It  was  shown  that  in  the  initial  state  with  the  zero  total  magnetic  moment  under  the  influence  the  alternating  magnetic  field,  various  regimes  of  the  induced  magnetic  moment  including  quasistatic  states  are  established.  Revealed  are  the  significant  differences  between  these  regimes  related  to  different  systems.  The  magnitude  and  direction  of  the  magnetic  moment  of  the  system,  as  well  the  states  of  dynamic  bistability,  have  been  investigated.

Ключевые  слова:  индуцированный  магнитный  момент;  динамическая  бистабильность;  система  диполей;  управление  намагниченностью 

Keywords:   induced  magnetic  moment;  dynamic  bistability;  system  of  dipoles;  control  of  magnetization

Системы  диполей  представляют  важный  объект  исследований  благодаря  созданию  новых  сред  при  внедрении  их  в  твердотельные  пористые  матрицы  [4,  6]  и  ввиду  формирования  на  их  основе  магнитных  жидкостей  [2].  В  свою  очередь  показано,  что  система  частиц  в  большинстве  случаев  испытывает  про­цесс  агрегации  с  формированием  за  счет  диполь-дипольного  взаимодействия  различных  по  объему  кластеров  [1,  7].  В  настоящей  работе  исследуются  сис­темы  с  нулевым  суммарным  магнитным  моментом,  состоящие  из  трех  и  четырех  магнитных  диполей.  Показано,  что  воздействие  переменного  поля  приводит  к  существенно  отличающимся  для  различных  систем  стационарным  режимам  индуцированного  магнитного  моменты,  включая  квазистатические  состояния.  Выявлены  возможности  управления  индуцированным  магнитным  моментом. 

Рассматривая  систему  диполей,  полагаем,  что  каждый  из  них  связан  с  другими  диполь-дипольным  взаимодействием  и  способен  вращаться  вокруг  своего,  остающегося  неподвижным,  центра  инерции.  Время  изменения  конфигурации  системы  в  целом  принимается  достаточно  большим,  чтобы  соответствующей  динамикой  можно  было  пренебречь.  Тела  предполагаются  однородными  и  шарообразными.  Принимая  диполи  идентичными  —  с  равными  по  модулю  дипольными  моментами    и  моментами  инерции  ,  —  запишем  уравнения  для  связанных  диполей  в  присутствии  внешнего  поля  : 

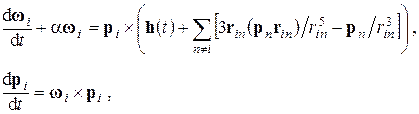       (1)

где:    —  угловая  скорость  i-го  диполя  (  —  угол  поворота  диполя  вокруг  оси  ), 

  —  параметр  диссипации; 

  —  вектор  между  i-го  и  n-го  диполей.  Далее  перейдем  к  безразмерным  параметрам  [6]:  ,  где  ,  a  —  характерный  параметр  конфигурации  системы;  при  этом  ;    —  нормированные  компоненты  магнитных  моментов;  остальные  параметры:  .  В  случае  кольцевых 

структур  при  числе  диполей  ,  устанавливается  только  одно  равновесное  состояние  —  с  нулевым  суммарным  магнитным  моментом    [5].  Проведем  анализ  влияния  переменного  поля  на  системы  из  3-х  и  4-х  диполей. 

При  возбуждении  системы  диполей  линейно  поляризованным  магнитным  полей    реализуются  различные  динамические  состояния.  На  рис.  1  приведена  ориентация  магнитных  моментов  систем  диполей,  возбуждаемых  переменным  полем  с  параметрами:  ,    (a,  b),  ,    (c,  d),  ,    (e,  f),  где  .  Видно,  что  в  случае  трех  диполей  направ­ление  индуцированного  магнитного  момента  системы  определяется  ориентацией  системы  относительно  поляризации  переменного  поля.  При  ориентационном  угле    (отсчитываемом  от  оси  y)  на  малых  частотах  постоянная  составляющая  магнитного  момента  располагается  под  углом  к  поляризации  поля  (a),  который  увеличивается  с  ростом  частоты,  и  начиная  с  некоторого  значения  W  она  оказывается  перпендикулярной  полю,  ориентируясь  вдоль  оси  x,  а  малые  колебания  испытывает  только  y-составляющая  магнитного  момента  (b).  Амплитуда  колебаний  на  рисунке  задается  непрерывным  и  пунктирным  векторами.  При  дальнейшем  росте  частоты  уменьшаются  как  модуль  вектора  ,  так  и  угол  его  отклонения,  и  на  достаточно  больших  частотах  индуцированный  магнитный  момент  можно  считать  постоянным  (вставка  на  рис.  3b).  При  повороте  системы  на  угол    (c)  магнитный  момент,  испытывая  по  модулю  низкоамплитуд­ные  колебания,  ориентируется  параллельно  поля,  т.  е.  вдоль  y.  В  этом  случае  могут  быть  реализованы  режимы  с  противоположной  ориентацией  «третьего»  диполя,  в  результате  возникает  динамическая  бистабильность  с  индуцирован­ными  магнитными  моментами  системы,  постоянная  составляющая  которых  от­личается  почти  на  две  единицы  (c,  d).  Следует  также  обратить  внимание  на  то,  что  имеет  место  бистабильность,  связанная  с  двумя  противоположными  направ­лениями  индуцированного  магнитного  момента;  в  частности,    на  рис.  1a,b  или    на  рис.  1c,d  могут  быть  как  положительными,  так  и  отрицательными. 

Рис.  1e  и  рис.  1f  отвечают  двум  типам  колебательных  режимов  индуцированного  магнитного  момента  системы  из  четырех  диполей  с  геометрией  квадрата,  устанавливаемых  при  различной  частоте  переменного  поля.  В  обоих  случаях  магнитный  момент  системы  ориентирован  вдоль  оси  y  (параллельно  полю),  но,  как  было  сказано,  при  малых  частотах  (e)  среднее  за  период  значение    отлично  от  нуля  и  значительно  превышает  амплитуду  колебаний,  тогда  как  в  режиме,  соответствующем  бóльшим  частотам  (f),  устанавливаются  колебания  относительно  нулевого  значения  ().  Первый  из  указанных  режимов  составляет  динамическую  бистабильность:  для  ,  также  как  и  в  случае  трехдипольной  системы,  возможно  два  противоположных  направления. 

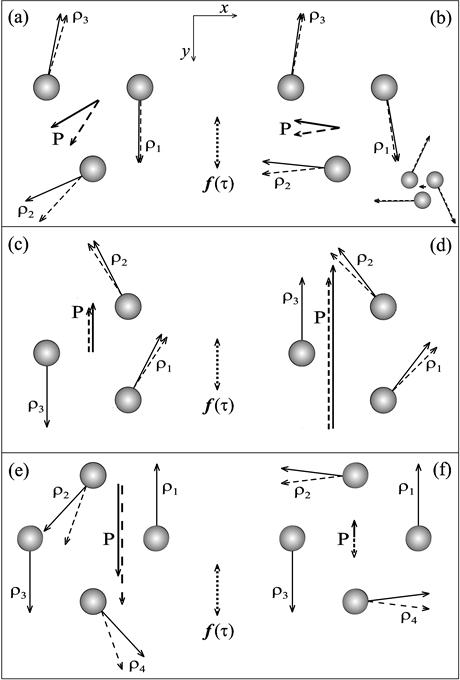
Рисунок  1.  Ориентация  магнитных  моментов  систем  диполей,  возбуждаемых  переменным  магнитным  полем

Индуцированный  магнитным  момент  четырехдипольных  квадратных  систем  всегда  направлен  параллельно  поляризации  переменного  поля.  В  случае  трехдипольных  систем  ориентация  магнитного  момента  определяется  частотой  и  амплитудой  поля,  а  также  ориентацией  системы  по  отношению  к  поляризации  поля.  На  рис.  2  представлены  зависимости  от  ориентационного  угла  x-  и  y-компонент  экстремумов  индуцированного  магнитного  момента  системы  трех 

диполей  при  параметрах  поля:  ,  ;  поляризация  поля,  как  и  в  остальных  случаях,  направлена  вдоль  оси  y;  в  качестве  исходного  состо­яния  принималось  равновесное  со­стояние  систем  при  данных  пара­метрах.  Видно,  что  на  относительно  малых  частотах  имеют  место  режимы  с  большим  –    –  и  малым  –    –  магнитными  моментами  (зависимость  1).  Режимы  с  большим  магнитным  моментом  реализуются  в  области  углов    (чем  меньше  частота  поля,  тем  больше  отвечающий  этим  режимам  интер­вал  значений  ориентационного  угла).  Причем  точно  при  указанных  углах  магнитный  момент  ориентирован  параллельно  полю  (),  а  при  отклонении  от  них  появляется  малая  по  величине  x-компонента  как  в  перемен­ной,  так  и  в  постоянной  составляющих  магнитного  момента.

Рисунок  2.  Зависимости  от  ориентационного  угла  x-  и  y-компонент  экстремумов  индуцированного  магнитного  момента  системы  3-х  диполей

Следует  заметить,  что  при    данный  режим  также  имеет  место  (устанавливается  ),  но  при  выбранных  параметрах  поля  из  равновесного  состояния  система  с  большей  вероятностью  переходит  в  другой  составляющий  бистабильность  режим  (в  режим  с  малым  магнитным  моментом),  а  для  получения  этого  режима  требуется  дополнительное  начальное  возмущение  (или,  например,  флуктуации  параметров  поля).  В  частности,  при  численном  моделировании  режим  с    для    из  равновесного  состояния  устанавливается  при  изменении  на  p  начальной  фазы  переменного  поля.  В  режиме  с    при    магнитный  момент  также  ориентируется  параллельно  полю,  но  при  отклонении  угла  y  от  указан­ных  значений  x-компонента  магнитного  момента  имеет  значительно  большую  величину,  чем  в  первом  рассмотренном  режиме. 

Во  всем  диапазоне  ориентационного  угла  имеет  место  динамическая  бистабильность,  и  при  изменении  на  p  начальной  фазы  переменного  поля  устанавливаются  режимы,  соответствующие  приведенным,  но  с  изменением  знака  компонент  магнитного  момента  и  смещенные  (вдоль  оси  ординат)  на  угол  .  Для  примера  на  рис.  2b  приведены  пунктиром  части  указанных  диаграмм  (зависимость  1),  полученные  для  данных  параметрах  системы  при  изменении  начальной  фазы  поля.  Следует  заметить,  что  в  одних  интервалах  ориентационного  угла  динамическую  бистабильность  составляют  режимы  с  сильно  отличающимися  значениями  индуцированного  магнитного  момента,  а  в  других  интервалах  —  режимы  с  приблизительно  одинаковыми  по  величине,  но  противоположно  направленными  магнитными  моментами.  В  случае  меньших  частот  в  трехдипольных  системах  имеет  место  другой  тип  режимов  (зависимость  2),  характеризующийся  отсутствием  больших  магнитных  моментов  (всегда  ),  но  при  этом  реализацией  режимов  с  перпендикулярной  поляризации  поля  ориентацией  постоянной  составляющей  магнитного  момента.  Последние  устанавливаются  при  ;  а  при  ,  как  и  в  ранее  рассмотренных  случаях,  индуцированный  магнитный  момент  параллелен  полю. 

Проведенный  анализ  показал,  что  для  систем  четырех  диполей  с  геометрией  квадрата  характерны  два  типа  динамических  режимом:  при  одних  режимах  индуцированный  магнитный  момент  системы  имеет  постоянную  и  сонаправленную  ей  переменную  составляющие,  в  режимах  второго  типа  (на  бóльших  частотах)  устанавливаются  колебания  магнитного  момента  системы  относительно  нулевого  значения,  амплитуда  которых  уменьшается  с  ростом  частоты  поля.  При  этом  независимо  от  частоты  и  амплитуды  переменного  поля,  а  также  от  ориентации  систем  в  плоскости,  суммарный  магнитный  момент  оказывается  параллельным  поляризации  приложенного  поля.  В  случае  трехдипольных  систем  в  зависимости  от  параметров  поля  индуцированный  магнитный  момент  может  устанавливаться  под  различными  углами  к  поляризации  поля.  При  этом  реализуются  режимы  с  наименьшими  по  амплитуде  колебаниями  магнитного  момента  —  магнитный  момент  остается  квазистатическим  даже  при  значительном  изменении  его  величины  за  счет  варьирования  параметров  поля. 

Таким  образом,  за  счет  изменения  параметров  внешнего  поля  для  сред  с  исходной  нулевой  намагниченность,  в  которых  рассмотренные  системы  выступают  в  роли  кластеров,  может  достигаться  эффективное  управление  индуциро­ванной  намагниченностью,  возникающей  при  воздействии  переменного  поля. 

С писок  литературы:

1.Гладких  Д.В.,  Диканский  Ю.И.  //  ЖТФ  —  2006  —  Т.  76  —  С.  13.

2.Головань  Л.А.,  Тимошенко  В.Ю.,  Кашкаров  П.К.//  УФН  —  2007  —  Т.  177  —  С.  619.

3.Лисовский  Ф.В.,  Полякова  О.П.  //  Письма  в  ЖЭТФ  —  2001  —  Т.  73  —  С.  546.

4.Шутый  А.М.  //  ЖЭТФ  —  2009  —  Т.  135  —  С.  1009.

5.Шутый  А.М.  //  ЖЭТФ  —  2010  —  Т.  137  —  С.  277.

6.Eliseev  A.A.,  Vyacheslavov  A.S.,  Lukashin  A.V.  et  al.  //  International  Journal  of  Nanoscience  —  2006  —  V.  5  —  P.  459.

7.Kozhevnikov  V.M.,  Chuenkova  I.J.,  Danilov  M.I.  et  al.  //  Magnetohydro-dynamics  —  2005  —  Т.  41  —  С.  53.