РАВНОВЕСНЫЕ  СОСТОЯНИЯ  КВАДРАТНЫХ  МАССИВОВ  ДИПОЛЕЙ  С  УЧЕТОМ  ОБМЕННОГО  ВЗАИМОДЕЙСТВИЯ

Шутый  Анатолий  Михайлович

д-р  физ.-мат.  наук,  вед.  науч.  сотр.  Ульяновского  государственного  университета,  РФ,  г.  Ульяновск

E -mail:  shuty@mail.ru

Семенцов  Дмитрий  Игоревич

д-р  физ.-мат.  наук,  профессор  Ульяновского  государственного  университета,  РФ,  г.  Ульяновск

E-mail: 

EQUILIBRIUM  CONDITIONS  OF  SQUARE  ARRAYS  OF  DIPOLES  WITH  ALLOWANCE  FOR  EXCHANGE  INTERACTION

Anatoliy  Shutyi

doctor  of  Physical  and  Mathematical  Sciences,  leading  research  scientist  of  Ulyanovsk  State  University,  Russia  Ulyanovsk

Dmitriy  Sementsov

doctor  of  Physical  and  Mathematical  Sciences,  professor  of  Ulyanovsk  State  University,  Russia  Ulyanovsk

Работа  выполнена  при  поддержке  министерства  образования  и  науки  РФ.

АННОТАЦИЯ

Проведен  численный  анализ  дипольных  решеток,  представляющие  собой  квадратные  массивы  магнитных  диполей.  Показано,  что  при  наличии  обменного  взаимодействия  между  магнитными  моментами  основными  равновесными  состояниями  являются  конфигурации  с  ориентацией  диполей  вдоль  диагонали  системы,  вдоль  ее  стороны,  а  также  конфигурации  с  вихревыми  структурами,  которые  могут  отличаться  по  расположению  центра  вихря.  Рассмотрены  условия  переходов  между  равновесными  конфигурациями  с  помощью  нормального  поля,  действующего  на  часть  входящих  в  систему  диполей. 

ABSTRACT

The  numerical  analysis  of  dipole  lattices  representing  square  arrays  of  magnetic  dipoles  has  been  conducted.  It  is  shown  that  in  case  of  exchange  interaction  between  magnetic  moments  the  main  equilibrium  conditions  are  configurations  with  orientation  of  dipoles  along  a  diagonal  of  a  system,  along  its  side  and  also  configurations  with  vortex  structures,  which  can  differ  by  a  disposition  of  the  centre  of  vortex.  Transitions  conditions  between  equilibrium  configurations  with  the  help  of  normal  field  affecting  a  part  of  dipoles  included  into  the  system  have  been  considered. 

Ключевые  слова:         решетки  магнитных  диполей;  обменное  взаимодействие;  равновесные  конфигурации.

Keywords:   lattices  of  magnetic  dipoles;  exchange  interaction;  equilibrium  configurations. 

Интерес  к  самоорганизующимся  системам,  в  том  числе  к  ансамблям  наночастиц,  приобрел  особое  значение  в  связи  с  достижениями  в  области  информационных  технологий  и  наноструктур.  Ансамбли  однодоменных  частиц  являются  также  удобными  объектами  для  изучения  фазовых  переходов  и  других  коллективных  эффектов.  Среди  них  особый  интерес  представляют  двумерные  сверхструктуры  в  виде  квадратных  решеток  наночастиц  [1].  В  настоящей  работе  исследуются  решетки,  являющиеся  квадратными  массивами  магнитных  диполей.  При  этом  рассмотрены  основные  равновесные  конфигурации,  которые  устанавливаются  в  данных  системах.  Выявлены  условия  переходов  между  равновесными  состояниями  решеток  под  воздействием  внешних  полей. 

При  рассмотрении  системы  диполей  полагаем,  что  они  связаны  диполь-дипольным  и  обменным  взаимодействиями,  и  каждый  из  них  может  поворачиваться  вокруг  центра  симметрии.  Положение  диполей  в  системе  принимается  неизменным,  тела  —  однородными  и  шарообразными.  Динамические  уравнения  для  системы  диполей  имеют  вид  [2—4]: 

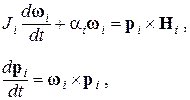                        (1)

где:    и    —  дипольный  магнитный  момент  и  угловая  скорость  i-го  диполя  (  —  угол  поворота  диполя  вокруг  оси  ), 

  —  момент  инерции, 

  —  параметр  диссипации;  поле,  создаваемое  в  месте  расположения  i-го  диполя  остальными  диполями  и  внешним  магнитным  полем  h: 

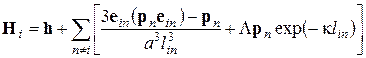  ,     (2)

где:    —  единичные  вектора  вдоль  направления, 

  —  вектор  между  положениями  i-го  и  n-го  диполей, 

  —  расстояние,  нормированное  на  характерный  параметр  конфигурации  системы  a  (в  рассматриваемых  системах  a  —  расстояние  между  соседними  диполями); 

Λ  и    —  константы  обменного  взаимодействия.  Магнитные  диполи  принимаются  идентичными:  ,  , 

.  Далее  перейдем  к  безразмерным  параметрам  [2]:  ,  ,  ,  где  дифференцирование  проводится  по  безразмерному  времени    ().  Компоненты  внешнее  поле  в  этом  случае  преобразуются  к  виду  ,  а  константа  обменного  взаимодействия  .  Динамические  уравнения  при  этом  приобретают  вид:

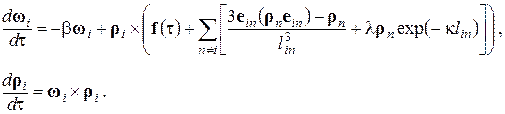         (3)

Исследование  массивов  диполей  показало,  что  в  случае  слабого  ()  обменного  взаимодействия  между  входящими  в  систему  телами  устанавлива­ются  равновесные  конфигурации  с  «седлообразной»  ориентацией  дипольных  моментов,  а  также  конфигурации,  в  центральной  области  которой  дипольные  моменты  составляют  пары  рядов  со  взаимно  противоположным  направлением.  Данные  равновесные  состояния  аналогичные  равновесным  состояниям  в  ди­польных  системах  без  обменного  взаимодействия.  В  случае  большого  обменного  взаимодействия  (  —  в  зависимости  от  систем)  равновесной  является  только  конфигурация,  в  которой  дипольные  моменты  выстраиваются  преиму­щественно  вдоль  диагонали  массива.  При  промежуточной  величине  обменного  взаимодействия  в  системах  могут  устанавливаться  как  диагональные  равновес­ные  конфигурации,  так  и  конфигурации  с  ориентацией  магнитных  моментов 

преимущественно  вдоль  стороны  массива,  а  также  конфигурации  с  вихревой  их  ориентацией.  Вихревые  равновесные  состояния  могут  отличаться  по  расположе­ния  в  массиве  цента  вихревой  структуры  и,  соответственно,  по  величине  суммарного  магнитного  момента  системы.  При  расположении  центра  вихря  в  центре  массива  с  четным  числом  диполей  суммарный  магнитный  момент  системы  равен  нулю;  при  смещении  вихря  к  краю  массива  его  дипольный  момент  увеличивается.  Наибольший  магнитный  момент  для  указанных  равно­весных  состояний  имеет  место  в  случае  диагональной  конфигурации.  Типичные  равновесные  конфигурации  массивов    и  ,  реализующиеся  при    

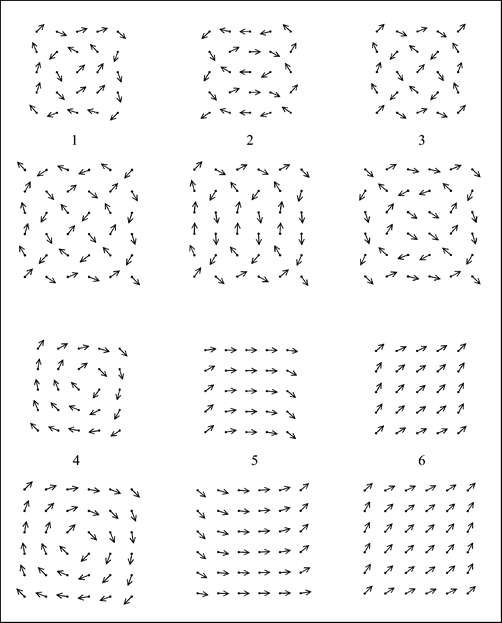
Рисунок  1.  Равновесные  конфигурации  массивов  ,  ;    (1—3)  и    (4—6)

(конфигурации  1—3)  и    (конфигурации  4—6),  приведены  на  рис.2.  Расчеты,  проведенные  для  других  массивов,  вплоть  до  систем  ,  показывают,  что  их  равновесные  конфигурации  подобны  приведенным. 

Рассмотрение  энергии  связи  показало,  что  наиболее  устойчивой  является  конфигурация  с  диагональной  ориентацией  диполей,  а  наименее  устойчивой  —  вихревая  конфигурация.

Рисунок  2.  Преобразования  между  равновесными  конфигурациями  с  помощью  нор­мального  к  системе  подмагничивающего  поля,  действующего  на  часть  диполей

С  помощью  действующего  на  всю  систему  плоскост­ного  магнитного  поля  реализуются  переходы  от  вихревой  конфигурации  к  диагональной  или  к  конфигурации  с  ориентацией  дипольных  моментов  вдоль  стороны  системы;  а  также  от  последней  к  диагональной  конфигурации.  В  слу­чае  диагональной  конфигурации  однородным  плоскостным  полем  достигается  только  перемагничивание  системы  —  изменение  ориентации  магнитного  момен­та  массива  —  с  сохранением  диагональной  структуры.  Переход  от  диагональной  конфигурации  к  вихревой  или  к  конфигурации  с  ориентацией  диполей  вдоль  стороны  массива  (и  от  последней  к  вихревой  конфигурации)  может  быть  реализован  с  помощью  магнитного  поля,  направленного  перпендикулярно  к  плоскости  системы  и  действующего  только  на  часть  входящих  в  массив  диполей. 

На  рис.  2  представлены  преобразования  между  равновесными  конфигура­ция  с  помощью  нормального  к  системе  поля.  Слева  приведена  исходная  кон­фигурация.  В  центре  –  конфигурация  перед  выключением  поля,  действующего  на  диполи,  представленные  в  виде  точек.  Справа  —  конечные  конфигурации  преобразования.  Из  рисунка  видно,  что,  здействуя  на  16  диполей  системы  ,  удается  перевести  диагональную  конфигурацию  в  вихревую  со  смещенным  центром  (a),  которая  затем  может  быть  переведена  в  вихревую  конфигурацию  (b).  Действие  нормального  поля  на  половину  диагональной  конфигурации  пере­водит  ее  в  конфигурацию  с  магнитным  моментом,  ориентированным  по  стороне  массива  (с).  Последняя  может  быть  преобразовала  в  вихревую  структуру  (d).  Смещение  центра  вихря  осуществляется  с  помощью  однородного  плоскостного  поля;  при  этом  направление  смещения  перпендикулярно  направлению  поля. 

Список  литературы:

1.Галкин  А.Ю.,  Иванов  Б.А.  //  Письма  в  ЖЭТФ  —  2006  —  Т.  83  —  С.  450.

2.Лисовский  Ф.В.,  Полякова  О.П.  //  Письма  в  ЖЭТФ  —  2001  —  Т.  73  —  С.  546. 

3.Шутый  А.М.  //  ЖЭТФ  —  2010  —  Т.  137  —  С.  277. 

4.Шутый  А.М.  //  Письма  в  ЖЭТФ  —  2013  —  Т.  97  —  С.  601.