Статья опубликована в рамках: XVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 02 апреля 2014 г.)
Наука: Физика
Секция: Оптика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ЦЕНТРИРОВАННАЯ ОПТИЧЕСКАЯ СИСТЕМА: МАТРИЧНЫЙ И ГРАФИЧЕСКИЙ МЕТОДЫ РАСЧЕТА
Васильчикова Елена Николаевна
канд. физ.-мат. наук, доцент Московского государственного областного университета, РФ, г. Москва
E -mail: envas2011@yandex.ru
Козеева Мария Ивановна
студент Московского государственного областного университета, РФ, г. Москва
CENTERED OPTICAL SYSTEM: MATRIX AND GRAPHIC METHODS
Vasilchikova Elena Nikolaevna
candidate of physical and mathematical sciences, associate professor of Moscow State Regional University, Russia, Moscow
Kozeeva Mariya Ivanovna
student of Moscow State Regional University, Russia, Moscow
АННОТАЦИЯ
Решение задачи о прохождении света через идеальную центрированную оптическую систему возможно различными способами. В данной работе приведены основные теоретические обоснования каждого метода, а также проведен сравнительный анализ различных методов расчета центрированных оптических систем в условиях параксиальных лучей на примере конкретной задачи.
ABSTRACT
Solution of problem of light passing through perfectly centered optical system is possible in different ways. In this paper we present the main theoretical underpinning of each method, we also provide a comparative analysis of different methods of calculation of centered optical systems with rays being paraxial rays applied to specific tasks.
Ключевые слова: центрированная оптическая система; параксиальные лучи; гомоцентрический пучок лучей; геометрический метод расчета; матричный метод расчета.
Keywords: centered optical system; paraxial rays; homocentric pencil of rays; geometric calculation method; matrix method of calculation.
В рамках геометрической оптики, распространение света описывается с помощью светового луча — линии, касательная к которой в каждой точке совпадает с направлением распространения световой энергии. Поэтому решение задач геометрической оптики сводится к определению хода световых лучей в оптических системах.
Наряду с традиционным расчетом существует матричный метод, позволяющий установить целый ряд соотношений между входными и выходными параметрами системы с помощью одной матрицы оптической системы. Выбор того или иного метода диктуется требованиями поставленной задачи.
Правило знаков. Отрезки, лежащие на оптической оси, имеют знак плюс, если отсчет совпадает с ходом луча (начало отсчета совпадает с вершиной сферической поверхности), в противном случае отрезок записывается со знаком минус. Углы отсчитываются от оптической оси, если отсчет идет по часовой стрелке, то угол записывается со знаком плюс, против часовой стрелки — со знаком минус.
Гомоцентрический пучок параксиальных лучей при прохождении через идеальную центрированную оптическую систему остается гомоцентрическим, поэтому для каждой точки предмета система формирует стигматическое (резкое) изображение.
1.1 Геометрический метод
Построение хода луча в оптической системе основано на правилах геометрической оптики, являющихся следствием закона преломления света на границе раздела сред в условиях параксиальных лучей (рисунок 1). Уравнение сопряженных точек сферической поверхности:
![]() (1)
(1)
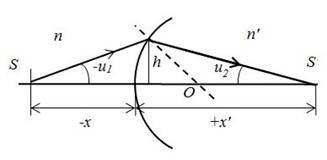
Рисунок 1. Ход луча на границе раздела сред в условиях параксиальных лучей для одной сферической поверхности
Здесь ![]() и
и ![]() — углы в пространстве предметов и изображений, n и n' — показатели преломления сред слева и справа от сферической поверхности. Величина
— углы в пространстве предметов и изображений, n и n' — показатели преломления сред слева и справа от сферической поверхности. Величина ![]() называется оптической силой сферической поверхности.
называется оптической силой сферической поверхности.
1.2 Матричный метод
Преобразование луча в оптической системе удобно описывать с помощью специальных матриц, которые вводятся следующим образом (3,4). Матрица преломления R для одной сферической поверхности (рисунок 1) имеет вид:
![]() .
.
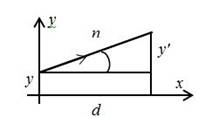
Рисунок 2. Введение матрицы перемещения Т
Матрица перемещения T между двумя опорными плоскостями, расположенными на расстоянии d друг от друга (рисунок 2) записывается в виде:
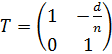 .
.
Матрица преобразования ![]() от предмета к изображению для одной сферической поверхности (рисунок 1) получится после перемножения трех матриц (верхний индекс 1 соответствует одной сферической поверхности):
от предмета к изображению для одной сферической поверхности (рисунок 1) получится после перемножения трех матриц (верхний индекс 1 соответствует одной сферической поверхности):
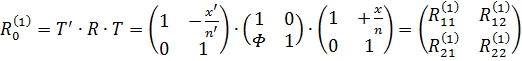 .
.
![]() (2)
(2)
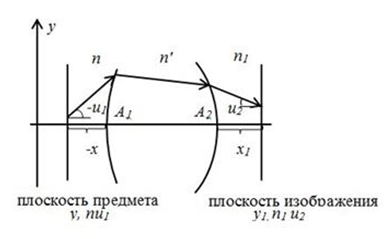
Рисунок 3. Ход луча на границе раздела сред в условиях параксиальных лучей для линзы
Важно отметить, что ![]() , в чем можно легко убедиться с помощью подстановки. Вводя увеличение
, в чем можно легко убедиться с помощью подстановки. Вводя увеличение ![]() и, учитывая условие
и, учитывая условие ![]() (необходимое для получения четкого изображения точки), матрица
(необходимое для получения четкого изображения точки), матрица ![]() может быть записана в виде:
может быть записана в виде: 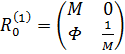 . Координаты главных плоскостей определяются условиями (3):
. Координаты главных плоскостей определяются условиями (3):
![]() (3)
(3)
Координаты фокальных плоскостей определяются условиями:
![]() . (4)
. (4)
Линза имеет в общем случае две сферических поверхности, поэтому матрица такой оптической системы (рисунок 3): ![]() , где
, где ![]() и
и![]() — матрицы преломления на 2-й и 1-й поверхностях линзы,
— матрицы преломления на 2-й и 1-й поверхностях линзы, ![]() — передаточная матрица (внутри линзы).
— передаточная матрица (внутри линзы). ![]() .
.
![]() (5)
(5)
Пусть параметры луча в плоскости предмета ![]() , тогда параметры луча в плоскости изображения определяются соотношением:
, тогда параметры луча в плоскости изображения определяются соотношением:
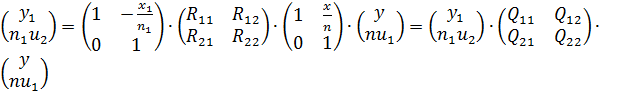 .
.
Компоненты матрицы преобразования от предмета к изображению:
![]()
![]()
Отметим, что ![]() . Из условия
. Из условия ![]() следует известная формула линзы
следует известная формула линзы ![]() Φ.
Φ.
Вводим аналогично случаю одной поверхности увеличение ![]() . Матрица преобразования
. Матрица преобразования ![]() принимает вид:
принимает вид: 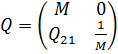 , где
, где ![]() — оптическая сила толстой линзы. Отсюда аналогично случаю одной поверхности определяются координаты кардинальных элементов (формулы (3), (4)).
— оптическая сила толстой линзы. Отсюда аналогично случаю одной поверхности определяются координаты кардинальных элементов (формулы (3), (4)).
1. Пример расчета центрированной оптической системы
Рассмотрим следующую задачу. На рисунке 4 представлена центрированная система, состоящая из трех тонких линз, находящихся в воздухе. Определить положение точки схождения параллельного пучка, падающего слева, после прохождения через систему.
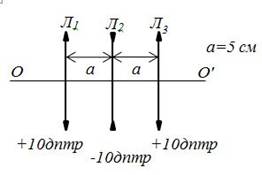
Рисунок 4. Центрированная система, состоящая из трех тонких линз, находящихся в воздухе
Решение выполним двумя способами: матричным и геометрическим.
Матричный расчет.
![]() — матрицы преломления 3-й и 1-й линз (собирающих);
— матрицы преломления 3-й и 1-й линз (собирающих);
![]() — матрица перемещения промежутков между линзами;
— матрица перемещения промежутков между линзами;
![]() — матрица преломления 2-й линзы (рассеивающей).
— матрица преломления 2-й линзы (рассеивающей).
Матрица оптической системы определяется как произведение матриц
![]() .
.
Искомое расстояние от линзы до фокуса определяется условием М=0 (4):
![]() .
.
Расстояние отсчитывается от линзы Л3 до фокуса F1.
Геометрический способ.
Луч падает слева параллельно оптической оси (рисунок 5).

Рисунок 5. Построение хода луча через систему трех линз
Дано:
![]() ;
;
![]() .
.
Определить: расстояние x.
Запишем уравнения сопряженных точек для каждой линзы системы и сложим их:
![]()
![]()
![]()
![]() (6)
(6)
Используя условия параксиальных лучей, получим из чертежа соотношения
![]() , которые после подстановки в (6) позволят найти расстояние x:
, которые после подстановки в (6) позволят найти расстояние x:
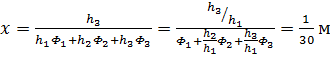 .
.
Сравнение двух методов решения позволяет сделать следующие выводы:
Матричный метод делает очень удобным использование вычислительной техники для расчета оптических систем, особенно при большом количестве линз в системе.
Графические и аналитические методы расчета эффективны для анализа общих закономерностей распространения света через оптическую систему.
Различные методы дают одинаковые результаты, так как в их основе лежат фундаментальные законы геометрической оптики.
Список литературы:
1.Джерард А. Введение в матричную оптику/ А. Джерард, Дж.М. Берч. М.: Мир, 1978. — 342 с.
2.Ландсберг Г.С. Оптика/ Г.С. Ландсберг. М.: Наука, 1976. — 926 с.
3.Матвеев А.Н. Оптика/ А.Н. Матвеев. М.: Высш. шк., 1985. — 351 с.
4.Сивухин Д.В. Общий курс физики. Оптика/ Д.В. Сивухин. М.: Наука, 1985. — 735 с.
дипломов


Оставить комментарий