Статья опубликована в рамках: XV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 февраля 2014 г.)
Наука: Физика
Секция: Механика жидкости, газа и плазмы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ ВРАЩАТЕЛЬНЫХ КОЛЕБАНИЙ ЦИЛИНДРА В ВОЗДУШНОМ ПОТОКЕ
Киселев Николай Андреевич
студент математико-механического факультета Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E-mail: kisnikn@mail.ru
Рябинин Анатолий Николаевич
д-р физ.-мат. наук, гл. научн. сотр. Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E-mail: a_ryabinin@front.ru
THE STUDY OF CYLINDER ROTATIONAL OSCILLATIONS IN THE AIRFLOW
Kiselev Nikolai
student, Faculty of Mathematics and Mechanics of St. Petersburg State University, Russia St. Petersburg
Ryabinin Anatoly
d.Sc, Principal Researcher, St. Petersburg State University, Russia St. Petersburg
АННОТАЦИЯ
Экспериментально исследуются вращательные колебания кругового цилиндра в воздушном потоке с целью их описания с помощью математической модели. Получены амплитуды колебаний и их период. Вычислены параметры математической модели.
ABSTRACT
Rotational oscillations of circular cylinder in the airflow are studied experimentally. The goal of study is the description of oscillations with the mathematical model. The amplitude of oscillations and their period are obtained. Model parameters are calculated.
Ключевые слова: воздушный поток; цилиндр; колебания; математическая модель.
Keywords: airflow; cylinder; oscillations; mathematical model.
Задача о колебаниях плохообтекаемых тел в воздушном потоке возникает, например, при транспортировке грузов, подвешенных под вертолетом. Одной из форм колебаний являются вращательные колебания тела вокруг вертикальной оси, проходящей через центр масс [2, 3, 5].
В настоящей работе экспериментально исследуются вращательные колебания кругового цилиндра. Эксперименты проводились в дозвуковой аэродинамической трубе АТ-12 Санкт-Петербургского государственного университета, описанной в работе [1]. В открытой рабочей части установки скорость воздушного потока может регулироваться в пределах от 0 до 40 м/с. Начальная степень турбулентности равна 0,4 %. Длина рабочей части 2,25 м, диаметр среза сопла круглого сечения 1,5 м.
Цилиндр диаметром 0,14 м и длиной L = 0,28 м, выполненный из дерева, закреплялся в рабочей части на проволочной подвеске таким образом, что он мог свободно вращаться вокруг горизонтальной оси, проходящей через центр цилиндра. Ось вращения перпендикулярна оси цилиндра и вектору скорости набегающего потока. К основанию цилиндра была прикреплена хвостовая державка, соединенная с двумя пружинами (рис. 1).
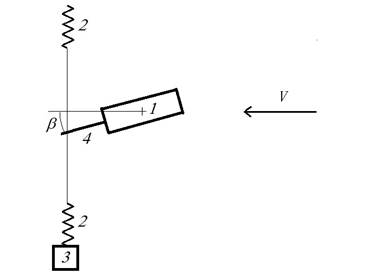
Рисунок 1. Схема эксперимента. 1 — цилиндр, 2 — пружины, 3 — полупроводниковый тензопреобразователь С-50, 4 — хвостовая державка
Нижняя пружина крепилась к полупроводниковому тензопреобразователю, предназначенному для измерения сил в диапазоне от 0 до 50 Н. Сигнал от тензопреобразователя подавался на осциллограф Velleman PCS500A, который, в свою очередь, был связан с компьютером. В положении равновесия угол ![]() принимал значения от 0 до 3 градусов. Зависимость натяжения пружины от времени записывалась в файл для дальнейшей обработки. Частота считывания равна 100 Гц, длительность записи — 17 секунд. Измерения затухающих колебаний проводились при отсутствии воздушного потока. Установившиеся колебания регистрировались при различных скоростях потока от 5 до 14 м/с и различных углах
принимал значения от 0 до 3 градусов. Зависимость натяжения пружины от времени записывалась в файл для дальнейшей обработки. Частота считывания равна 100 Гц, длительность записи — 17 секунд. Измерения затухающих колебаний проводились при отсутствии воздушного потока. Установившиеся колебания регистрировались при различных скоростях потока от 5 до 14 м/с и различных углах![]() . Процедура градуировки позволила пересчитать амплитуды колебаний натяжения пружины в амплитуды вращательных колебаний. Во всех случаях установившихся колебаний форма колебаний была близка к гармонической и период колебаний T = 0,74 с не зависел от скорости набегающего потока. Таким же периодом характеризовались затухающие колебания цилиндра в отсутствие потока. При обработке результатов измерений была принята модель вращательных автоколебаний цилиндра в потоке, предложенная в работе [4]:
. Процедура градуировки позволила пересчитать амплитуды колебаний натяжения пружины в амплитуды вращательных колебаний. Во всех случаях установившихся колебаний форма колебаний была близка к гармонической и период колебаний T = 0,74 с не зависел от скорости набегающего потока. Таким же периодом характеризовались затухающие колебания цилиндра в отсутствие потока. При обработке результатов измерений была принята модель вращательных автоколебаний цилиндра в потоке, предложенная в работе [4]:
|
|
|
где: A — амплитуда вращательных колебаний,
![]() — скорость набегающего потока,
— скорость набегающего потока,
![]() — параметр модели, описывающий влияние аэродинамических сил,
— параметр модели, описывающий влияние аэродинамических сил,
k2 — параметр модели, описывающий вязкое сопротивление упругой подвески,
µ — безразмерный коэффициент. Если скорость потока в формуле (1) положить равной нулю, получится уравнение (2) для амплитуды затухающих колебаний
|
|
|
имеющее экспоненциальное решение. Экспериментально полученная зависимость A от времени в полулогарифмических координатах приведена на рис. 2. Величина ![]() , определенная по наклону аппроксимирующей прямой на рис. 2, равна 0,13 с-1.
, определенная по наклону аппроксимирующей прямой на рис. 2, равна 0,13 с-1.
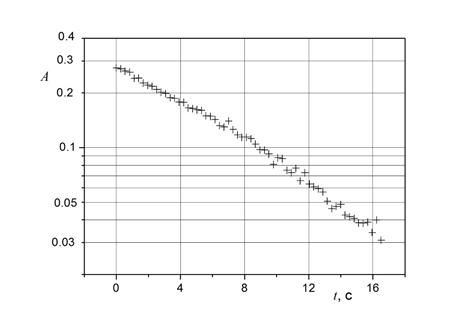
Рисунок 2. Зависимость амплитуды затухающих колебаний (в радианах) от времени в отсутствие потока в рабочей части.
Полагая в формуле (1)![]() , можно получить уравнение для амплитуды установившихся колебаний, которое преобразуется к виду
, можно получить уравнение для амплитуды установившихся колебаний, которое преобразуется к виду
|
|
|
Как и предсказывает формула (3), экспериментальные точки на графике рис. 3 для всех углов ![]() ложатся в пределах экспериментальной погрешности на одну прямую. Методом наименьших квадратов найдены коэффициенты линейной зависимости A2/4+β* от 1/v и определены параметры
ложатся в пределах экспериментальной погрешности на одну прямую. Методом наименьших квадратов найдены коэффициенты линейной зависимости A2/4+β* от 1/v и определены параметры ![]() = 65,3 и k2 = 14,5.
= 65,3 и k2 = 14,5.
Определена также величина безразмерного параметра математической модели колебаний цилиндра в воздушном потоке µ = 0,018.
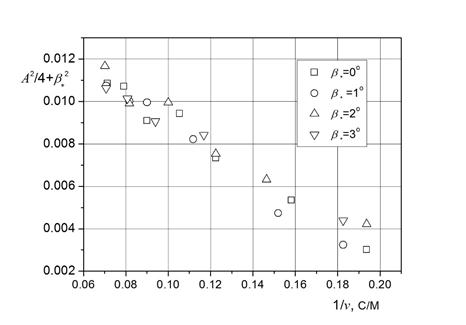
Рисунок 3. Зависимость A2/4+β* от 1/v
Таким образом, в результате эксперимента в аэродинамической трубе найдены все параметры математической модели, описывающей колебания кругового цилиндра в воздушном потоке.
Список литературы:
1.Ковалев М.А. О расчете и исследовании аэродинамических труб // Уч. зап. Ленингр. ун-та. — 1939. — Вып. 7. — С. 61—86.
2.Рябинин А.Н. Колебания маятника со стабилизатором в воздушном потоке // Вестн. С.-Петерб. ун-та. Сер. 1. — 1997. — Вып. 2. — С. 71—77.
3.Рябинин А.Н. Некоторые задачи аэродинамики плохообтекаемых тел. СПб.: Изд-во С.-Петербург. ун-та. 1997. — 142 с.
4.Рябинин А.Н., Лущенко И.В. Экспериментальные исследования колебаний цилиндра в воздушном потоке // Вестник СПбГУ. Сер. 1, — 2007. — Вып. 2. — С. 120—123.
5.Рябинин А.Н., Тюрин Б.Ф. Поведение груза, подвешенного под вертолетом // Вестн. С.-Петерб. ун-та. Сер. 1, — 1993. — Вып. 1. — С. 87—91.
дипломов


 ,,,l;’
,,,l;’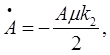 ,,,l;’
,,,l;’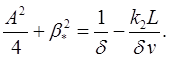 ,,,l;’
,,,l;’
Оставить комментарий