ОПРЕДЕЛЕНИЯ  ОПТИМАЛЬНЫХ  ВЕЛИЧИН  НАТЯГОВ  И  ДОПУСКАЕМОГО  ВНУТРЕННОГО  ДАВЛЕНИЯ  В  СОСТАВНЫХ  КОНСТРУКЦИЯХ,  СОЕДИНЕННЫХ  С  НАТЯГОМ

Годжаев  Тофик  Байрам  оглы

д-р  техн.  наук,  зав.  кафедрой  «Машинная  инженерия  и  организация  перевозок  в  транспорте»,  профессор  Азербайджанского  технологического  университета,  Республика  Азербайджан,  г.  Гянджа

E-mail:  Ilkin-540@mail.ru

Алиев  Шакир  Гусейнгулу  оглы

канд.  техн.  наук,  доцент  кафедры  ««Машинная  инженерия  и  организация  перевозок  в  транспорте»,  доцент  Азербайджанского  Технологического  Университета,  Республика  Азербайджан,  г.  Гянджа

E-mail: 

DEFINITIONS  OF  OPTIMAL  VALUES  OF  PRELOADS  AND  ALLOWABLE  INTERNAL  PRESSURE  IN  COMPOSITE  CONSTRUCTIONS  CONNECTED  WITH  A  PRELOAD

Tofik  Godzhaev

doctor  of  Engineering  Science,  Head  of  the  Department  of  Mechanical  Engineering  and  transport  shipments,  professor  of  Azerbaijan  Technological  University,  Republic  of  Azerbaijan  Gyanja

Shakir  Aliyev

candidate  of  Engineering  Science,  associate  professor  of  the  Department  of  Mechanical  Engineering  and  transport  shipments,  Azerbaijan  Technological  University,  Republic  of  Azerbaijan  Gyanja

AННОТАЦИЯ

В  статье  рассматриваются  определения  оптимальных  величин  и  допускаемого  внутреннего  давления  в  составных  конструкциях,  соединенных  с  натягом.  Дана  методика  определения  оптимальных  величин  и  допускаемого  внутреннего  давления.  Определено,  что  при  замене  однородной  составной  пластинки  (с  учётом  на­тяга),  эквивалентное  напряжение  уменьшается  и  увеличивается  прочность.

ABSTRACT

The  article  considers  definitions  of  optimal  values  and  allowable  internal  pressure  in  composite  constructions  connected  with  a  preload.  A  methodics  for  defining  optimal  values  and  allowable  internal  pressure  is  given.  It  is  found  that  in  case  of  replacement  of  a  homogeneous  composite  plate  (taking  preload  into  consideration)  equivalent  voltage  decreases  and  resistance  increases. 

Ключевые  слова:  напряжение;  прочность;  пластины;  давление;  натяг.

Keywords:  voltage;  resistance;  plates;  pressure;  preload. 

Современная  техника  предъявляет  повышенное  требование  к  прочностным  свойствам  машин,  конструкции  и  сооружений,  минимизации  затрат  материалов  и  максимальное  использование  ресурсов.

С  целью  повышения  прочностных  характеристик,  экономии  материалов,  снижения  веса  и  конструкции  иногда  требуется  создание  их  элементов  из  кусочно-однородных  деталей,  соединённых  между  собой  напряжённой  посадкой.  В  этих  соединениях  детали  хорошо  центрируются,  прочность  и  надёжность  при  динамических  и  знакопеременных  нагрузках  увеличиваются,  они  обладают  демпфирующей  способностью.  Благодаря  этим  и  другим  преимуществам,  соединения  с  натягом  нашли  весьма  большую  область  применения  в  самых  различных  конструкциях.  Поэтому  разработка  эффективных  методов  расчёта  на  прочность  составных  деталей,  соединённых  между  собой  прессовой  посадкой,  является  актуальной.

  С  целью  достижения  наибольшей  прочности,  в  рассматриваемых  составных  пластинках  наименьшей  материалоёмкости,  для  заданных  внутренних  давлений,  на  основе  квадратной  пластинки  (рис.  1),  рассмотрим  методику  определения  оптимальных  величин  натягов  δr_j  (j=2,  3,  5,  6);  причём  δr₂=δr₄  и  δr₃=δr₅  и  внутреннего  давления  Р₀  .

На  основе  принципа  суперпозиции,  величины  полных  напряжений  σ_r  и  σ_θ,  действующих  в  составной  пластинке,  равны  алгебраической  сумме  [1,  с.  78]  полученных  напряжений,  т.  е. 

и  затем,  для  наглядности,  построены  в  отдельности  их  эпюры.

Рисунок  1.  Cоставная  пластинка

С  учётом  натягов  δr₂  и  δr₃  (где  δr₅=δr₂  и  δr₆=δr₃),  напряжение  σ_θ  уменьшается  и,  наряду  с  этим,  рассматриваемая  пластинка  будет  выдерживать  сравнительно  большее  внутреннее  давление.

Величины  натягов  δr₅=δr₂  и  δr₆=δr₃  при  заданном  внутреннем  давлении  подбираем  таким  образом,  чтобы  распределение  напряжений  σ_θ  вдоль  вещественной  оси  квадратной  пластинки  было  бы,  по  возможности,  практически  равномерным.

Для  этого  приравниваем  между  собой  результирующие  напряжения  в  непосредственной»  [2,  с.  43]  близости  слева  от  точек  А,  В  и  С  (рис.  2),  т.  е.

Таблица  1.

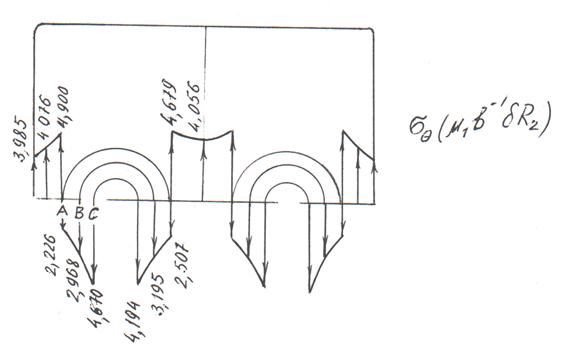
Рисунок  2.Эпюра  напряжений  составных  пластинок

Результирующие  напряжения  σ_θ  в  точках  А,  В  и  С  для  рассматриваемой  пластинки  соответственно  равны:

где  , 

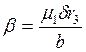
При  заданных  внутренних  давлениях  Р₄=Р₇=Р  из  условий  и  ,  для  определения  α  и  β,  составляем  систему  уравнений,  т.  е.:

Решая  её,  получим:  α=0,031Р,  β=0,0485Р

Отсюда

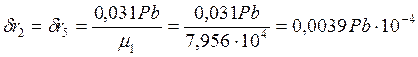
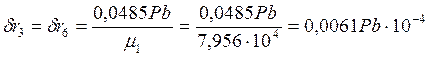
Далее,  при  найденных  значениях  натягов  в  характерных  точках  плас­тинки,  определены  величины  результирующих  напряжений  σ_r  и  σ_θ  (таблица)  и  для  наглядности  построены  эпюры  напряжений  σ_r  и  σ_θ  (рис.  3  и  4). 

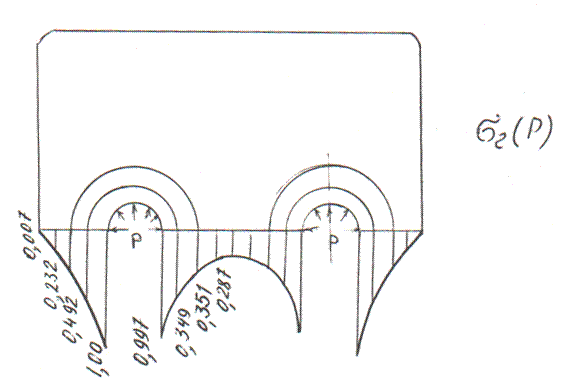
Рисунок  3.  Эпюра  напрежений  составных  пластинок

Из  рис.  4  наглядно  видно,  что  окружное  напряжение  по  вещественной  оси  распределяется»  [3,  с.  58]  почти  равномерно.

Далее  согласно  III  теории  прочности,  в  наиболее  напряжённой  точке  для  однородной  (без  натяга)  и  составной  (с  натягом)  пластинок,  напряжения  σ_θ  соответственно  равны:

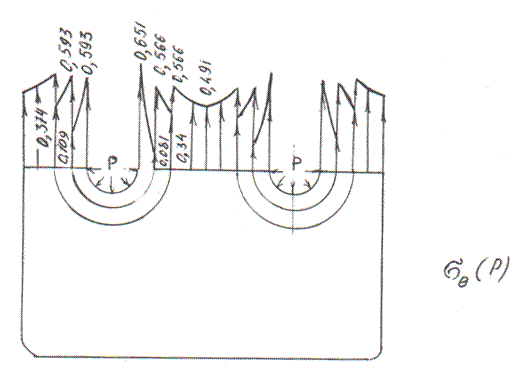
Рисунок  4.  Эпюра  напрежений  составных  пластинок

Таким  образом,  при  замене  однородной  пластинки  составной  (с  учётом  на­тяга),  эквивалентное  напряжение  уменьшается

,

т.  е.  эквивалентное  напряжение  уменьшается  в  раз  и  соответственно  увеличивается  прочность.  Затем,  определим  допускаемое  давление  Р_допус.

Отсюда 

R₂  =  R₄  =0,35b  ,R₃  =  R₅  =0,25b  ,R₀  =R₆  =0,15b

e  =0,45b,  µ₁  =  µ₂  =  µ₃  =  µ₄  =  µ₅

δR₃  =  δR₅≠  0  ,  P  ≠  0

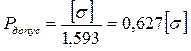
Так  как  все  составные  части  пластинки  изготовлены  из  стали–3,  при  этом  [σ]=160  МПа,  тогда

Р_допус.≤100  МПа

Таким  образом,  при  выше  найденных  натягах  δr₂  и  δr₃,  допускаемое  внутреннее  давление  не  должно  превышать  100  МПа.

На  основании  результатов  многочисленных  примеров  при  различных  вариантах  выяснено,  что  с  увеличением  количества  запрессованных  колец,  с  учётом  действия  внутренних  давлений,  соответственно  уменьшаются  значения  возникающих  напряжений  и  соответственно  увеличивается  прочность  рассматриваемого  объекта,  а  также  путём  варьирования  эксцентриситета  запрессованных  шайб,  можно  определить  оптимальный  вариант  места  расположения  шайб.

Список  литературы:

1.            Амензаде  Ю.А.  К  вопросу  об  упругом  равновесии  кусочно-однородных  тел.  Прикладная  механика,  т.II.,  вып.10,  1966  —  с.  69—70.

2.            Годжаев  Т.Б.,  Алиев  Ш.Г.  Концентрация  напряжений  в  кусочно-однородной  пластинке  различной  конфигурации  от  двух  эксцентрично  запрессованных  круглых  шайб,  центрально  ослабленных  отверстием  различной  формы  //  Национальная  Академия  Наук  Азербайджана.  Гянджинский  Региональный  Научный  Центр  «Сборник  Известий»  №  29.  Гянджа-2007,  —  стр.  111—114.

3.            Годжаев  Т.Б.,  Алиев  C.Г.,  Алиев  Ш.Г.  К  вопросу  исследования  концен­трации  напряжений  в  квадратной  пластинке  от  центрально  посаженного  упругого  кольца,  симметрично  ослабленного  двумя  круглыми  отверстиями  //  Азербайджанский  Технологический  Университет,  «Научные  вести»  №  5—6,  Гянджа  2007,  —  стр.  65—69.