Статья опубликована в рамках: XIV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 15 января 2014 г.)
Наука: Физика
Секция: Механика жидкости, газа и плазмы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ФИЛЬТРАЦИОННЫЕ ВОЛНЫ В АНИЗОТРОПНОЙ СРЕДЕ
Филиппов Александр Иванович
д-р техн. наук, профессор СФ БашГУ, РФ, Республика Башкортостан, г. Стерлитамак
E-mail: filippovai@rambler.ru
Ахметова Оксана Валентиновна
канд. физ.-мат. наук, доцент СФ УГНТУ, РФ, Республика Башкортостан, г. Салават
E-mail: ahoksana@yandex.ru
Ковальский Алексей Алексеевич
советник ректора БашГУ, РФ, Республика Башкортостан, г. Уфа
E-mail: aakov68@mail.ru
Повленкович Рената Фанилевна
студент СФ УГНТУ, РФ, Республика Башкортостан, г. Салават
FILTRATION WAVES IN ANISOTROPIC ENVIRONMENT
Filippov Alexandr Ivanovich
doctor of engineering sciences, professor of Bashkir State University, Republik of Bashkortostan, Sterlitamak
Akhmetova Oksana Valentinovna
candidate of phys.-mathem. sciences, associate professor of Ufa State Petroleum
Technological University, Republik of Bashkortostan, Salavat
Kovalskiy Aleksey Alekseevich
advisor to the rector of Bashkir State University, Republik of Bashkortostan, Ufa
Povlenkovich Renata Fanilevna
student of Ufa State Petroleum Technological University, Republik of Bashkortostan, Salavat
АННОТАЦИЯ
Получено уравнение для описания фильтрационно-волновых процессов в аксиально симметричной пористой среде. Найдены выражения для скорости волны, коэффициентов пьезопроводности и затухания в соответствии с выбранными координатными линиями.
ABSTRACT
An equation to describe the filtration-wave processes in an axially symmetric porous medium is acquired. The expressions for the wave velocity, attenuation coefficients and diffusivity in accordance with the selected coordinate lines is found.
Ключевые слова: фильтрация; закон Дарси; фильтрующаяся жидкость; анизотропная среда; фильтрационно-волновое поле давления.
Keywords: filtration, Darcy's law, fluid filters, anisotropic medium, filtration wave field.
При стационарной фильтрации истинная скорость может быть найдена из закона Дарси [1], который для анизотропной среды, пренебрегая полями сил тяжести и других массовых сил, в цилиндрической системе координат при осевой симметрии записывается в виде
|
|
(1) |
Соотношение (1) эквивалентно наличию фиктивных сил трения [2]
|
|
(2) |
В случае нестационарной фильтрации необходимо учесть действие указанных сил трения, тогда получим уравнение движения
|
|
(3) |
Сила ![]() , согласно (2), зависит от скорости фильтрации, поэтому из (3) получим уравнение движения жидкой фазы
, согласно (2), зависит от скорости фильтрации, поэтому из (3) получим уравнение движения жидкой фазы
|
|
(4) |
которое в частном случае совпадает с уравнением Эйлера-Жуковского. Если же полное ускорение жидкой фазы равно нулю, то нетрудно убедиться, что из (4) следует закон Дарси (1).
Закон изменения (сохранения) массы фильтрующейся жидкости при отсутствии источников записывается в форме уравнения неразрывности
|
|
(5) |
При наличии источников уравнение (5) изменяется — в правой части возникает функция источников массы.
Приведенные выше выражения позволяют получить уравнения, описывающие фильтрационно-волновые явления в пористых средах. Для этого линеаризуем исходные уравнения. Во втором слагаемом (5) полагаем приближенно , в итоге получим
|
|
(6) |
Уравнение движения (4) далее покоординатно умножаем на соответствующие коэффициенты проницаемости, также полагаем , и, пренебрегая слагаемыми второго порядка по скорости, имеем
|
|
(7) |
С уравнениями (6) и (7) осуществим следующие преобразования. Подействуем оператором набла на векторное уравнение (7)
|
|
(8) |
Подставив выражение ![]() , найденное из уравнения (6) в (8), получим
, найденное из уравнения (6) в (8), получим
|
|
(9) |
Дальнейшие преобразования первого слагаемого осуществим в предположении, что компоненты тензора проницаемости не зависят от пространственных координат и времени
|
|
(10) |
Для слабо анизотропной среды, когда разница между компонентами тензора проницаемости много меньше их полных значений, двумя последними слагаемыми в (10) можно пренебречь, тогда уравнение запишется как
|
= |
(11) |
Повторив замену для дивергенции вектора скорости из линеаризованного уравнения неразрывности в полученном уравнении, имеем
|
= |
(12) |
Для линеаризованных уравнений состояния для жидкой фазы ρ = ρ(P,T) = ![]() и скелета ρs = ρs(P,T) =
и скелета ρs = ρs(P,T) = ![]() баротропное приближение для произведения плотности жидкости на пористость может быть представлено в линеаризованной по давлению форме [3]
баротропное приближение для произведения плотности жидкости на пористость может быть представлено в линеаризованной по давлению форме [3]
|
|
|
С учетом этого уравнение для поля давления в анизоторопной однородной среде представляется в виде
|
|
(13) |
Заметим, что уравнение (13) содержит перед вторым слагаемым в левой части среднее по осям значение проницаемости ![]() .
.
Найденное уравнение позволяет определить две скорости распространения фильтрационной волны, относящиеся к соответствующим координатам
 ,
, 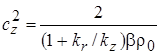 ,
,
и соответствующие коэффициенты пъезопроводности
![]() ,
, ![]() .
.
Сжимаемость пористой среды β выражается через сжимаемости жидкости и скелета. Поскольку массу скелета в контрольном объеме приближенно можно считать постоянной, то имеем ![]() , что позволяет выразить зависимость пористости от плотности скелета
, что позволяет выразить зависимость пористости от плотности скелета ![]() или давления
или давления ![]() :
: ![]() ,
, ![]() . С учетом этих выражений преобразуем производную по времени в левой части уравнения (6) как
. С учетом этих выражений преобразуем производную по времени в левой части уравнения (6) как
|
|
(14) |
Отсюда следует выражение для сжимаемости пористой среды ![]() . Здесь
. Здесь ![]() ,
, ![]()
![]() — значения плотности жидкости, материала скелета и давления в точке линеаризации.
— значения плотности жидкости, материала скелета и давления в точке линеаризации.
Путем сопоставления полученного уравнения с классическим уравнением колебаний определена величина коэффициента затухания
|
|
(15) |
Итак, фильтрационно-волновое поле давления в однородной анизотропной пористой среде в указанных выше приближениях описывается уравнением
|
|
(16) |
или
|
|
(17) |
Список литературы:
1.Маскет М. Физические основы технологии добычи нефти. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003 — 606 с.
2.Филиппов А.И., Короткова К.Н. Волновые поля давления в пласте и скважине // Физика волновых процессов и радиотехнические системы. — 2009. — Т. 12. — № 1. — С. 48—53
3.Филиппов А.И., Ахметова О.В., Заманова Г.Ф. Асимптотические представления упругих волновых полей в проницаемых пластах // Акустический журнал. — 2013. — Т. 59. — № 5. — C. 596—606
дипломов


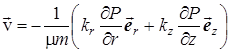 .
. .
. .
. ,
, .
.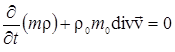 .
. .
. .
.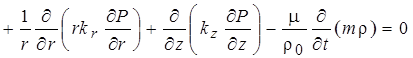 .
.
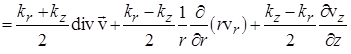 .
.
 .
.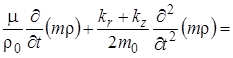
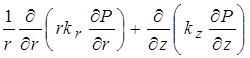 .
.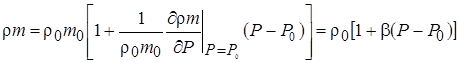 ,
, 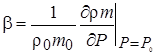 .
.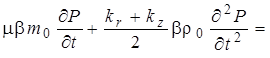
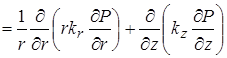 .
.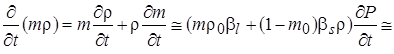
 .
.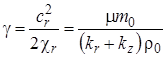 .
.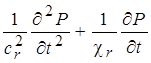
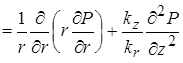 ,
,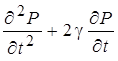
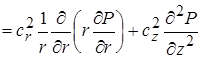 .
.
Оставить комментарий