СЖАТИЕ  ИЗОБРАЖЕНИЙ  С  ПОМОЩЬЮ  КВАДРАТИЧНЫХ  КРИВЫХ  БЕЗЬЕ

Анисимова  Эллина  Сергеевна

магистр  прикладной  математики  и  информатики,  ассистент  кафедры  информатики  и  дискретной  математики  Елабужского  Института  Казанского  Федерального  Университета,  РФ,  Республика  Татарстан,  г.  Елабуга

E-mail: 

IMAGE  COMPRESSION  USING  A  QUADRATIC  BEZIER  CURVES

Anisimova  Ellina

Master  of  Applied  of  Mathematics  and  Informatics,  assistant  Department  of  Computer  Science  and  Discrete  Mathematics  of  Yelabuga  Institute  of  the  Kazan  Federal  University,  Russian  Federation,  Republic  of  Tatarstan,  Yelabuga

АННОТАЦИЯ

В  данной  статье  рассматривается  метод  фрактального  сжатия  изображений,  основанный  на  обнаружении  самоподобных  участков  в  изображении.  В  качестве  системы  итерируемых  функций  используется  система  квадратичных  кривых  Безье.

ABSTRACT

In  this  report  we  describe  a  method  of  fractal  image  compression  based  on  the  detection  of  self-similar  areas  in  the  image.  As  a  system  of  iterated  function  system  is  used  quadratic  Bezier  curves.

Ключевые  слова:  фрактал;  фрактальное  сжатие;  квадратичные  кривые  Безье;  неподвижная  точка.

Keywords:  fractal;  fractal  compression;  quadratic  Bezier  curves;  fixed  point.

Одним  из  методов  цифровой  стеганографии  (направление  классической  стеганографии,  основанное  на  сокрытии  или  внедрении  дополнительной  информации  в  цифровые  объекты)  является  метод  фрактального  кодирования  изображений.  Идея  фрактального  кодирования  состоит  в  замене  самого  изображения  некоторым  сжимающим  отображением,  для  которого  исходное  изображение  (или  некоторое  близкое  к  нему)  является  неподвижной  точкой,  а  для  восстановления  достаточно  многократно  применить  это  отображение  к  любому  стартовому  изображению.  По  теореме  Банаха,  такие  итерации  всегда  приводят  к  неподвижной  точке,  то  есть  к  исходному  изображению  [2,  с.  48].

В  качестве  системы  итерируемых  функций  используем  систему  отображений  с  помощью  квадратичных  кривых  Безье:

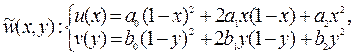                (1)

где  a₀,  a₁,  a₂,  b₀,  b₁,  b₂Î[0,1].

Исследование  проведём  в  пакете  прикладных  математических  программ  SciLab.  В  качестве  исходного  изображения  возьмём  изображение  размерности  256х256.  Применим  к  нему  базовый  алгоритм  фрактального  кодирования  [1,  с.  3].

Разобьём  изображение  на  неперекрывающиеся  ранговые  блоки  методом  квадродерева.  Установим  максимальную  глубину  квадродерева  равной  6. 

Покрываем  изображение  размерности  128х128  (после  применения  к  нему  выборки)  последовательностью  доменных  блоков  —  прямоугольников.  Количество  строк  и  столбцов  устанавливаем  равными  16,  горизонтальное  и  вертикальное  перекрывания  —  половинными. 

Для  каждого  рангового  блока  находим  домен  и  соответствующее  преобразование,  которое  наилучшим  образом  покрывает  ранговый  блок  (рис.  1).

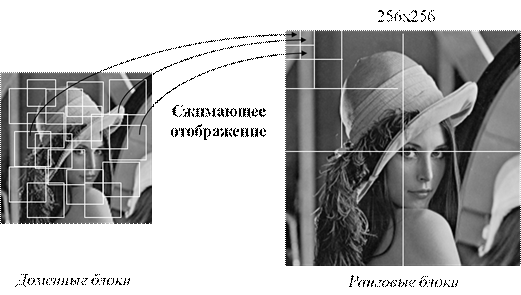
Рисунок  1.  Отображение  доменных  блоков  изображения  в  ранговые  блоки

Посредством  интерполяции  определяем  значения  пикселов  в  доменном  блоке  после  отображения.  Вычисляем  контрастность,  яркость  и  значение  ошибки.  Если  значение  ошибки  оказывается  меньше  допустимой  погрешности,  значит,  ранговый  блок  покрыт  с  допустимой  погрешностью,  записываем  в  текстовый  файл  номер  домена,  коэффициенты  преобразования  Безье,  значения  яркости  и  контрастности.  Переходим  к  следующему  ранговому  блоку. 

Для  реализации  итерационной  схемы  декодирования  определим  два  массива  изображений:  domen  и  im.  В  качестве  массива  domen  можно  взять  любое  начальное  изображение.  Содержимое  каждого  рангового  блока  вычисляется  применением  преобразования  к  соответствующему  доменному  блоку  и  хранится  в  массиве  im.  Одна  итерация  завершается,  когда  обработаны  все  ранговые  блоки.  Перед  началом  новой  итерации  необходимо  заменить  массив  domen  массивом  im,  массив  im  очистить.

Рисунок  2.  Декодирование  изображения  с  начальным  однородным  изображением

Рисунок  3.  Декодирование  изображения  с  произвольным  начальным  изображением

Вне  зависимости  от  начального  изображения,  итерации  сходятся  к  одной  и  той  же  неподвижной  точке  (рис.  2,  3).

Средняя  пиксельная  ошибка  после  предварительного  сжатия  обоих  изображений  (исходного  и  декодированного)  до  размеров  64х64  равна  0,026.  Стандартная  количественная  оценка  искажений  25,4Дб.

Таким  образом,  было  проведено  фрактальное  сжатие  изображения  с  использованием  среды  SciLab  на  основе  квадратичных  кривых  Безье,  вычислены  количественные  оценки  искажений.

Список  литературы:

1.            An  Introduction  to  Fractal  Image  Compression:  Texas  Instruments  Europe,  1997,  —  20  p.

2.            Welstead,  Stephen.  Fractal  and  Wavelet  Image  Compression  Techniques  //  SPIE.  Washington  DC,  USA,  2009,  —  320  p.