Статья опубликована в рамках: XIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 09 декабря 2013 г.)
Наука: Биология
Секция: Физиология
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНЫХ ПОПУЛЯЦИОННЫХ РЕАКЦИЙ ОДНОКЛЕТОЧНЫХ
Захаров Игорь Сергеевич
канд. техн. наук, доцент кафедры Инженерной защиты окружающей среды, Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И. Ульянова (Ленина), РФ, г. Санкт-Петербург
E-mail: sergeich188@gmail.com
Величко Анна Николаевна
аспирант кафедры Инженерной защиты окружающей среды, Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И. Ульянова (Ленина), РФ, г. Санкт-Петербург
MATHEMATICAL MODELING OF POPULATION THEMPERATURE REACTION OF SIMPLES
Igor Zakharov
d.Ph., assistant of professor, Environmental Protection Engineering department, Saint-Petersburg State Electrotechnical University, Russia Saint-Petersburg
Anna Velichko
Postgraduate student, Environmental Protection Engineering department, Saint-Petersburg State Electrotechnical University, Russia Saint-Petersburg
АННОТАЦИЯ
Цель — исследование термотаксиса одноклеточных организмов. Метод — моделирование движения популяции на базе метода клеточных автоматов и экспериментальная проверка адекватности модели. Результат — моделирование нескольких видов таксиса, получение графиков модельных распределений количества клеток по кювете, коррелирующих с полученными результатами обработки снимков термотаксиса инфузорий P. caudatum.
ABSTRACT
Purpose — study of unicellular organism’s thermotaxis. Method of modeling the movement of the population based on cellular automata method and experimental validation of the model. Result — modeling of several kinds of taxis, obtaining graphs model distributions number of cells on the cell correlated with the results of image processing thermotaxis ciliates P. caudatum.
Ключевые слова: модель; клеточные автоматы; термотаксис; инфузория.
Keywords: model; cellular automata; thermotaxis; ciliate.
Исследование термотаксиса одноклеточных и его математическое описание является важной проблемой естествознания. Современные исследования показали возможность обнаружения с помощью термотаксиса инфузорий вредных факторов в среде [4].
Его особенностью является перемещение организмов в зону комфортных температур [6]. Наиболее широко используется для изучения термотаксиса метод Гертера [5], основанный на выявлении диапазона комфортных температур при движении организмов в условиях температурного градиента.
Целью данной статьи является разработка метода моделирования термотаксиса одноклеточных, как реакции, отражающей процесс терморегуляции.
В задачи исследования входила разработка подхода к моделированию разновидностей популяционного движения организмов на базе модели клеточных автоматов и проверка ее адекватности в эксперименте при организации термотаксиса инфузорий P.caudatum.
Для математического описания термотаксиса была выбрана дискретная модель клеточных автоматов [1], которая нашла применение в разных областях естествознания. Клеточные модели используются для описания биологических процессов от возбудимой среды распространения импульса в сердечных нервных узлах [3] до модели процесса образования из амеб-слизевиков плодового тела, которое движется по градиенту температуры [7], и формы сигналов, получаемых в результате перемещения популяции инфузорий при многократном изменении полярности напряжения на электродах [2].
Моделирование проводилось на основе результатов обработки цифровых снимков термотаксиса P.caudatum, полученных при различных расположениях зоны комфортных температур.
Построение линейной рекуррентной клеточной модели. Пусть зона перемещения популяции инфузорий состоит из n ячеек (Яn), в которых первоначально находится одинаковое количество частиц (Nlk — количество частиц в ячейке l при отсчете k, при k=1 Nl1 = 150), что моделирует равномерное распределение организмов в узкой протяженной кювете.

Рисунок. 1. Модель зоны перемещения популяции инфузорий, состоящая из 8 ячеек (а) и цифровой снимок слоя взвеси инфузорий Р. caudatum в кювете (б)
Частицы (моделирующие инфузорий) могут перемещаться из одних ячеек в другие через каждый отсчет времени, причем суммарное количество частиц остается постоянным. Зададимся значениями коэффициентов перехода в ячейках αij, которые переходят из ячейки i в ячейку j при движении популяции (см. таблица 1). Их значения и знаки определяют скорость и направление движения частиц из одной ячейки в другую.
Таблица 1.
Описание модели
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Моделирование ненаправленного движения частиц
Значения коэффициентов перехода для картины популяции в контроле задавались методом имитационного моделирования, т. е. генерировались случайные числа с нормальным распределением со средним равным 0 и СКО = 0,005. При моделировании были получены графики распределения частиц по всем ячейкам (рисунок 2 а) с волнами, характерными для реальной картины распределений яркости вертикальных срезов (∑ЯПВ) пикселей на снимке популяций инфузорий (рисунок 2 б) после усреднения методом скользящего среднего.

Рисунок 2.Распределение частиц по ячейкам при отсутствии направленного перемещения (а) и распределения яркостей пикселей по слою инфузорий в кювете 40´5´10 мм (б)
Моделирование одностороннего движения частиц при зоне комфортной температуры в крайней ячейке
Коэффициенты перехода частиц из ячеек имеют значения αij ≠ αji. В зависимости от того αij больше или меньше αji, изменяется направление движения. Последовательности зон 1—8 присваиваются значения температурного градиента от максимальной температуры в диапазоне толерантности до минимальной.
Модель отражает уменьшение частиц по зонам кюветы при увеличении количества частиц возле температурного источника с комфортной температурой, как и полученное в эксперименте распределение при движении P. caudatum в зону уменьшения температуры (от источника со льдом, слева).
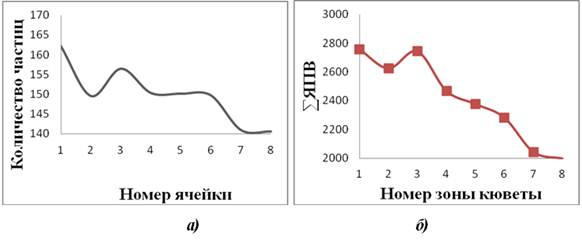
Рисунок 3. Распределения частиц при движении в зону 1 (а) и яркостей пикселей снимка слоя инфузорий в кювете 40´5´10 мм при зоне комфортной температуры слева (б)
Корреляция между результатами эксперимента и моделью составила 0.91 при параметрах αij среднее=0,5, СКО=0,001, а для αji среднее=0,2, СКО=0,001.
Моделирование двухстороннего направленного движения частиц при зоне комфортной температуры в центре
Двухстороннее движение было промоделировано изменением значений коэффициентов перехода так, чтобы они представляли зеркальное отражение относительно центральной ячейки (рисунок 4 а). Подбор функции изменения коэффициентов с аддитивной добавкой случайной составляющей позволяет получить график распределения частиц по ячейкам (рисунок 4 б, где черные столбцы — коэффициенты αij, серые — αji). Была получена высокая корреляция модельного распределения (r=0,94) с полученным в эксперименте распределением яркостей пикселей вертикальных, в котором регистрировался термотаксис P. caudatum при расположении зоны комфортных температур в центре кюветы. (Цифровые изображения обработаны методом скользящего среднего).
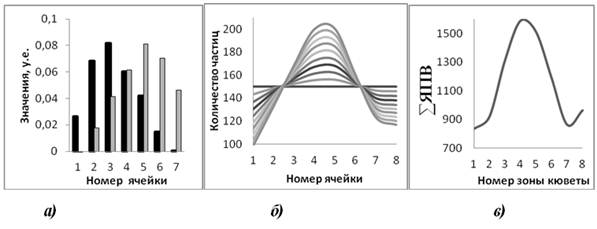
Рисунок 4. Коэффициенты перехода (а), модель распределения частиц по кювете (б) и сглаженный график распределения яркостей пикселей по вертикали (в)
Заключение
Разработанная математическая модель популяционных реакций одноклеточных позволила моделировать ненаправленное, одностороннее и двустороннее направленное движение организмов. Модель позволила анализировать как за счет изменения коэффициентов перехода групп одноклеточных организмов из одной зоны в другую меняется распределение количества клеток по кювете. Было показано, что для распределений популяции P.caudatum при термотаксисе, полученных после цифровой обработки его снимков, моделирование позволяет получить с коэффициентом корреляции r=0,91…0,94 полиномы, описывающие распределение частиц по ячейкам, за счет подбора коэффициентов перехода частиц из ячеек.
Модель допускает усложнение условий движения популяции: формирование сложного движения, учет градиента фактора, стрессовых факторов, токсичности среды и др., которые влияют на движение популяции.
Разработанная модель может быть полезна для биологических исследований, а также для биотестирования качества среды.
Список литературы:
1.Данилов Ю.А. Джон фон Нейман. М.: Знание, 1981. — С. 272.
2.Захаров И.С., Казанцева А.Г. Разработка и экспериментальная проверка математических моделей динамики гальванотаксиса инфузорий для биотестирования водных сред // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. — 2011. — Вып. 10. — С. 99—104.
3.Тоффоли Т., Марголус Н. Машины клеточных автоматов, М.: «Мир», 1991.
4.Gordon C.J. Temperature and toxicology : an integrative, comparative, and environmental approach. // CRC Press, 2005. — P. 256—257.
5.Dr. Konrad Herter. Untersuchungen über den temperatursinn einiger insekten. // Ausdem zoologischen Institut der Universitat GSttlngen und dem zoologischen Institut der Universitut Berlin. Germany. 1923. — P. 221—288.
6.Malvin G.M. et al. Nitric Oxide Production and Thermoregulation in Paramecium caudatum. — Acta Protozoologica — Internation Journal on Protistology. 2003. 42: 259—267.
7.Maree A.F.M., Panfilov A.V., Hogeweg P. Migration and Thermotaxis of Dictyoselium discoideum Slugs, a Model Study // Journal of theoretical Biology. — 1999. — № 199. — P. 297—309.
дипломов


Оставить комментарий