МОДЕЛИРОВАНИЕ  КВАДРУПОЛЬНОГО  ОРИЕНТАЦИОННОГО  ПОРЯДКА  В  ГРЕБНЕОБРАЗНЫХ  ПОЛИМЕРАХ

Шевченко  Светлана  Сергеевна

канд.  физ.-мат.  наук,  доцент  каф.  физики  филиала  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail: 

Костин  Иван  Владимирович

канд.  физ.-мат.  наук,  доцент  каф.  физики  филиала  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail:  ivk20062006@yandex.ru

Нилова  Людмила  Ивановна

зав.  каф.  физики  филиала  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail: 

quadrupole  orientation  order  modeling  in  comb-shaped  polymers

Svetlana  Shevchenko

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

Ivan  Kostin

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

Lyudmila  Nilova

head  of  the  chair  of  Physics  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

АННОТАЦИЯ

Развита  теория  продольных  релаксационных  процессов,  связанных  с  локальной  ориентационной  упорядоченностью  сегментов  полимерных  цепей,  состоящих  из  жестких  кинетических  единиц,  находящихся  в  протяженном  двумерном  слое  конечной  толщины  при  «полусвободных»  граничных  условиях  для  концов  цепей.  Рассчитана  зависимость  параметра  квадрупольного  порядка  как  функция  длины  развязки  боковой  группы,  которая  достаточно  хорошо  согласуется  с  экспериментальными  данными  по  исследованию  методом  ЯМР  упорядоченности  в  полиметакрилатах,  содержащих  фенилбензольные  мезогенные  группы.

ABSTRACT

There  has  been  advocated  the  theory  of  long  relaxation  processes  connected  with  local  orientation  relationship  of  polymer  segments,  which  consist  of  rigid  kinetic  units.  These  units  are  in  the  extended  finite  two-dimensional  layer  in  terms  of  semifree  border  conditions  for  chain  ends.  Dependence  of  quadrupole  order  parameter  as  a  function  of  coupling  length  of  a  pendent  group  has  been  calculated,  which  correlates  very  accurately  with  the  experiment  data  on  NMR  studies  of  ordering  in  polymethacrylates  consisting  phenyl  benzene  mesogenic  groups. 

Ключевые  слова:  гребнеоборазные  полимеры;  квадрупольный  порядок;  длина  развязки  боковой  группы

Keywords:  comb-shaped  polymers;  quadrupole  order;  coupling  length  of  a  pendent  group. 

Исследование  конформационных  и  динамических  свойств  поверхностных  мезофазных  структур  представляет  актуальный  интерес  в  связи  с  существованием  приграничных  монослоев,  ориентированных  пленок,  отдельных  макромолекул  в  разбавленных  растворах  гребнеобразных  полимеров,  b-слоев  в  полипептидах  и  др.  Для  ряда  практических  задач,  особенно  при  сравнении  с  экспериментом,  представляется  необхо­димым  рассмотреть  ориентационное  поведение  и  динамику  движений  конечных  цепей  или  их  участков.  Существует  множество  экспериментальных  данных,  указывающих  на  значительное  влияние  длины  боковых  групп  на  свойства  анизотропии  и  скорость  релаксационных  процессов  в  разбавленных  растворах  гребнеобразных  полимеров,  требующих  теоретической  интерпретации.  В  данной  работе,  изучаются  закономерности  упорядоченности  сегментов  взаимодействующих  полимерных  цепей  с  жесткостью  на  изгиб,  состоящих  из  жестких  кинетических  единиц,  находящихся  в  конечных  двумерных  системах  (слоях),  в  зависимости  от  положения  сегмента  в  цепи,  соотношения  констант  локальных  внутри-  и  межцепных  взаимодействий. 

В  используемой  в  работе  многоцепной  модели  ориентационно  упорядоченного  слоя  предполагается  [1,  2],  что  достаточно  большое  число  M  полимерных  цепей  конечной  длины  находятся  в  одной  плоскости  —  двумерной  «квазирешетке»  (рис.  1).  Каждая  цепь  состоит  из  N  жестких  кинетических  единиц,  которые  могут  ориентироваться  на  фоне  вязкой  среды.  Если  эту  модель  применить  к  описанию  упорядоченного  состояния  макромолекул  гребнеобразных  полимеров,  то  параметр  N  характеризует  длину  боковых  цепей,  а  число  M  пропорционально  длине  основной  цепи  соответственно  (рис.  1). 

Рисунок  1.  Модель  двумерного  полимерного  протяженного  слоя  конечной  толщины,  содержащего  M  полужестких  цепей  с  конечной  контурной  длинной  N

Ориентацию  жестких  кинетических  единиц  цепей  в  двумерной  системе  можно  характеризовать  дипольным  параметром  порядка

  (1)

где  угол    определяет  ориентацию  n-ой  единицы,  расположенной  в  m-ой  цепи,  относительно  выделенного  в  плоскости  «квазирешетки»  (n,  m)  направления  (например,  направления  преимущественного  упорядочения  цепей)  (рис.  1).  В  работе  использованы  «полусвободные»  граничные  условия,  налагаемые  на  ориентацию  концов  любой  цепи  в  слое  ,  ,  которые  можно  использовать  для  моделирования  упорядочения  и  локальной  подвижности  цепей  в  поверхностных  слоях  на  межфазных  границах  (жидких  и  твердых  поверхностях),  сравнительно  коротких  цепей,  ориентированных  на  подложке  или  боковых  мезогенных  групп  в  разбавленных  растворах  гребнеобразных  полимеров.

При  большом  внутри-  и  межмолекулярного  ориентационном  порядке  кинетические  единицы  цепей  совершают  заторможенные  продольные  колебания  вблизи  минимума  дипольного  потенциала,  для  которого  углы  поворотов  соседних  единиц  относительно  друг  друга  являются  достаточно  малыми:    рад  и    рад.  В  этом  (низкотемпературном)  приближении  эффективная  потенциальная  энергия  внутри-  и  межцепного  взаимодействий  ближайших  единиц  цепей  для  рассматриваемой  многоцепной  модели  имеет  вид  [1]:

,         (2)

где  энергетическая  константа  К_l  связана  с  термодинамической  жесткостью  цепей  на  изгиб,  характеризуемой  числом  жестких  кинетических  единиц  в  сегменте  Куна  длиной  А  [1]:  ,  а  соответствующая  (в  «поперечном»  направлении  слоя  m)  константа  K_t  характеризует  локальные  межцепные  ориентационные  взаимодействия  единиц,  находящихся  в  соседних  цепях.

Во  многих  экспериментальных  методах  исследования  упорядоченности  в  полимерных  системах  определяется  квадрупольный  параметр  порядка

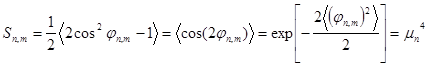,  (3)

который  удобно  вычислять  по  значению  дальнего  порядка  ,определяемого  выражением  (1)  [3].  Экспериментальное  подтверждение  результатов  расчета  упорядоченности,  полученных  в  данной  работе,  можно  получить  при  объяснении  закономерностей  ориентационного  порядка  в  боковых  группах  гребнеобразных  полимеров,  содержащих  гибкие  мезогенные  развязки,  исследованных  методом  ЯМР  в  работе  [3].  Цель  этой  работы  заключалась  в  изучении  ориентационного  поведения  во  внешнем  магнитном  поле  нескольких  гомологов  ряда  ЖК-полимеров,  содержащих  фенилбензольные  мезогенные  группы.  В  работе  отмечается,  что  только  эксперименты  с  гомологическими  рядами  дают  возможность  получить  количественную  информацию  о  влиянии  молекулярного  строения  мезогенных  фрагментов  на  ориентационный  порядок  в  ЖК-полимерах.  Одним  из  результатов  работы  [3]  был  вывод  о  том,  что  параметр  порядка  в  исследуемых  полимерах  не  зависит  от  степени  полимеризации  основной  цепи  и  от  их  молярной  массы.  Следовательно,  для  изучения  свойств  таких  полимеров  является  допустимым  использование  модели  бесконечно-протяженного  слоя  ()  конечной  толщины  (N),  используемой  в  данной  работе.  Кроме  этого,  в  работе  [3]  было  обнаружено  монотонное  уменьшение  параметра  порядка  при  удлинении  концевой  боковой  группы  (за  счет  увеличения  длины  гибкоцепной  алифатической  развязки),  и  указано  на  отсутствие  в  последние  15  лет  в  литературе  каких-либо  данных,  объясняющих  наблюдаемое  поведение  параметра  порядка,  в  частности  отсутствие  эффекта  «чет-нечет»  при  изменении  длины  развязки  в  боковой  группе.

С  целью  теоретической  интерпретации  наблюдаемых  закономерностей,  для  модели  полимерного  конечного  слоя  при  граничных  условиях  «полусвободные  концы»,  лучше  всего  подходящих  для  описания  поведения  гребнеобразных  полимеров,  была  рассчитана  зависимость  параметра  квадрупольного  порядка    от  длины  развязки  (n)  боковой  группы.  Для  более  точного  соответствия  расчетных  и  экспериментальных  данных  следует  учесть  тот  факт,  что  при  удлинении  боковой  цепи  увеличивается  число  единиц  в  статистическом  сегменте  Куна  (параметр  a  в  данной  модели),  что  обнаружено  в  ряде  экспериментальных  работ  по  исследованию  свойств  гребнеобразных  полимеров  методом  диэлектрической  релаксации  (ДР)  [4].  В  таблице  1  при  фиксированном  значении  параметра  межцепных  взаимодействий  b  приводится  зависимость  персистентной  длины  a  от  n  —  длины  боковой  цепи,  которая  описывает  этот  гомологический  ряд  полимеров  в  рамках  данной  модели.

Таблица  1.

Зависимость  эффективной  термодинамической  жесткости  цепи  на  изгиб  a  от  длины  боковой  развязки  n  для  гребнеобразных  полимеров  P1—P4  при  фиксированном  значении  параметра  межцепных  взаимодействий  (b=0,5)

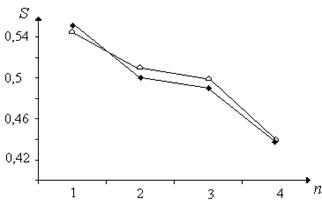
Рисунок  2.  Зависимость  параметра  квадрупольного  порядка  S  для  гребнеобразных  ЖК  полиметакрилатов  от  длины  алифатической  развязки  (n):  экспериментальные  данные  по  ЯМР  [3]  ()  и  теоретические  расчеты  ().

На  рис.  2.  представлено  сопоставление  экспериментальных  и  рассчитанных  значений  параметра  порядка  S  в  зависимости  от  длины  боковых  групп  (n).  Видно,  что  полученная  теоретическая  зависимость  достаточно  хорошо  согласуется  с  имеющимися  экспериментальными  данными  и  действительно  демонстрирует  отсутствие  эффекта  «чет-нечет»  для  гребнеобразных  ЖК-полиметакрилатов.

Список  литературы:

1. Шевченко  С.С.  Дис…канд.  физ.  -  мат.  наук.  СПб.:  РГПУ,  2005.
2. Maximov  A.V.,  Shevchenko  S.S.,  Maximova  O.G.,  Gotlib  Yu.Ya.  Macromolecular  Symposia,  2001,  63,  309. 
3. Barmatov  E.B.  Journal  of  Polymer  Science,  2002,  40,  2044.
4. Бурштейн  Л.Л.,  Шибаев  В.П.  Высокомолек.  соед.  А.,  1982,  25  ,  3.