РАССИНХРОНИЗАЦИЯ  ЧАСОВ  ПОСТУПАТЕЛЬНО  ДВИГАЮЩЕЙСЯ  ЖЁСТКОЙ  СИСТЕМЫ  ОТСЧЁТА

Войтик  Виталий  Викторович

аспирант  Башкирского  Государственного  Педагогического  Университета,  РФ,  республика  Башкортостан,  г.  Уфа

E-mail: 

GRADUAL  CLOCK  SKEW  BY  MEANS  OF  MOVING  RIGID  REFERENCE  SYSTEM

Vitaliy  Voytik 

post  graduate  student  of  Bashkir  State  Pedagogical  University  named  after  M.  Akmulla,  Russian  Federation,  the  Republic  of  Bashkortostan  Ufa

АННОТАЦИЯ

В  статье  двумя  способами  вычисляется  рассинхронизация  в  лабораторной  системе  двух  часов:  покоящихся  в  начале  отсчёта  жёсткой  системы  отсчёта  и  в  удалённой  точке.  Один  из  этих  методов  общерелятивистский,  второй  —  использует  кинематическое  замедление  времени.  В  результате  рассинхронизация  двух  часов  зависит  от  вектора  расстояния  между  часами  и  некоторого  векторного  коэффициента  зависящего  от  конкретного  закона  движения  начала  отсчёта.

ABSTRACT

In  the  article  clock  skew  in  laboratory  system  of  two  hours  has  been  calculated:  centering  at  a  starting  point  of  rigid  reference  system  and  in  remote  point.  The  first  out  of  these  methods  is  general  relativistic  while  the  second  uses  kinematic  time  dilation.  As  a  result  clock  skew  of  two  hours  depends  on  a  distance  vector  between  hours  and  on  some  kind  of  vector  index,  which  depends  on  a  particular  law  of  starting  point  movement. 

Ключевые  слова:  преобразование  Лоренца-Мёллера-Нэлсона;  рассинхронизация  часов.

Keywords:  Lorentz  transformation;  clock  skew.

Специальное  преобразование  между  лабораторной  инерциальной  системой  отсчёта    и  неинерциальной,  поступательно  двигающейся  без  вращения  (относительно  лабораторной  системы)  жёсткой  системой  s:  выглядит  в  виде  [5]

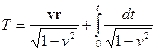  ,  (1)

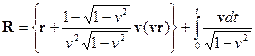  .  (2)

При  этом  собственное  ускорение  этой  системы  отсчёта    есть  [4]

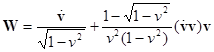,       (3)

а  угловая  скорость  собственного  вращения    совпадает  с  собственной  частотой  прецессии  Томаса 

,    (4)

В  [2]  была  вычислена  скорость  движения  в  лабораторной  системе  точек  системы  s.  Она  равна 

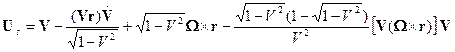.  (5)

Для 

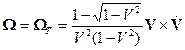  (6)

скорость  точек  системы  координат  s  равна

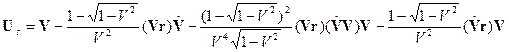,  (7)

где:    —  скорость  начала  отсчёта  s,  .  В  [3]  была  вычислена  зависимость  векторного  параметра    от  координат  системы  s 

.  (8)

Рассинхронизацию  физических  часов  расположенных  в  разных  точках  системы  координат  s  и  рассматриваемую  в  лабораторной  системе  отсчёта  можно  объяснить  двояко.  Одно  из  объяснений  этого  эффекта  заключается  в  различной  скорости  хода  часов  расположенных  в  положении  с  отличающимся  гравитационном  потенциалом.  Действительно,  вычислим  дифференциал  физического  времени  прошедшего  в  точке  с  координатой  .  Он  равен

  (9)

где   является  координатным  временем,  а    определяется  из  интервала

.  (10)

Это  время    можно  вычислить  дифференцируя  уравнение  (1)  полагая  при  этом  .  В  результате  получим,  что

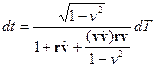.  (11)

Далее,  из  уравнения  (3)  следует,  что

  (12)

Подставим  это  выражение  в  (11)  и  найдём  значение  дроби  оставляя  только  члены  с  первой  степенью  собственного  ускорения.  Получим,  что

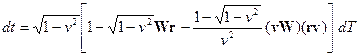.  (13)

Далее,  вычислим  значение    также  оставляя  члены  только  с  первой  степенью  по .  Учитывая  (8)  имеем

.  (14)

Подставив  (14)  в  (13)  окончательно  получим  следующее  значение  для  дифференциала  координатного  времени  dt

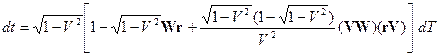.  (15)

Физическое  же  время    согласно  (9)  и  (10)  в    раз  больше  чем  координатное.  Поэтому

  (16)

и  рассинхронизация  часов  в  точке  с  координатой    и  в  начале  отсчёта  будет

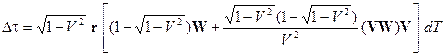.  (17)

Данный  эффект  можно  объяснить  также  и  чисто  кинематическим  образом.  Он  появляется  из-за  неоднородности  движения  разных  точек  системы  отсчёта  s.  Например,  для  рассинхронизации  часов  за  время    в  начале  отсчёта  и  в  точке  с  координатой    величина  рассинхронизации  будет  равна

,  (18)

что  при  учёте  равенства  (7),  составит  величину 

.  (19)

Подставив  сюда 

  (20)

можно  заметить,  что  (19)  и  (17)  эквивалентны.  Если  подставить  в  (19)  выражения  (6)  и

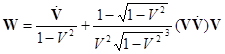,  (21)

то  можно  выразить  величину  рассинхронизации  двух  часов  через  скорость  и  лабораторное  ускорение  начала  отсчёта

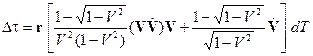.  (22)

Для  прямолинейного  движения  системы  отсчёта  (22)  можно  проинтегрировать.  В  результате  рассинхронизация  равна

.  (23)

Данное  значение  рассинхронизации  было  уже  найдено  в  [1].  В  общем  же  случае  рассинхронизация  часов  зависит  от  конкретного  закона  движения  начала  отсчёта.

Список  литературы:

1.Войтик  В.В.  О  влиянии  ускорения  на  прямолинейное  движение  жёсткого  стержня.  2.  Рассинхронизация  часов//  Вест.  Чел.  гос.  унив.  Физика,  —  2011.  —  №  7  (222).  —  вып.  9.  —  с.  50—54 

2.Войтик  В.В.  О  движении  точек  жёсткой  системы  отсчёта.  Сборник  материалов  II  Международной  научно-практической  конференции  студентов,  аспирантов  и  молодых  учёных  «Шаг  в  будущее:  теоретические  и  прикладные  исследования  современной  науки»  26—27  ноября  2013  г.,  научно-издательский  центр  «Открытие»  г.  СПб.

3.Voytik  V.V.  On  a  special  transformation  to  a  non-inertial,  radially  rigid  reference  frame//  Grav.  and  Cosm.,  —  2013  —  №  3.  —  p.  193—200.

4.Voytik  V.V.  The  general  form-invariance  principle//  Grav.  and  Cosm.,  —  2011.  —  v.  17.  —  №  3.  —  p.  218—223.

5.Nelson  R.A.  Generalized  Lorentz  transformation  for  an  accelerated,  rotating  frame  of  reference//  J.  Math.  Phys.,  —  1987.  —  №  28.  —  p.  2379—2383.