РАСЧЕТ  ФИЗИЧЕСКИХ  ХАРАКТЕРИСТИК  ИЗОТРОПНОГО  ИЗЛУЧАТЕЛЯ  В  ОДНОРОДНОЙ  БЕЗГРАНИЧНОЙ  СРЕДЕ

Шевченко  Светлана  Сергеевна

канд.  физ.-мат.  наук,  доцент,  филиал  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail: 

Костин  Иван  Владимирович

канд.  физ.-мат.  наук,  доцент,  филиал  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail:  ivk20062006@yandex.ru

Нилова  Людмила  Ивановна

заведующий  кафедрой  физики,  филиал  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail:  samurasam@rambler.ru

Андреева  Наталья  Владимировна

доцент  кафедры  физики,  филиал  Военной  Академии  Министерства  обороны,  РФ,  г.  Череповец

E-mail: 

ISOTROPIC  RADIATOR  PHYSICAL  CHARACTERISTICS  CALCULATION  IN  HOMOGENEOUS  UNBOUNDED  MEDIUM

Svetlana  Shevchenko

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

Ivan  Kostin

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

Lyudmila  Nilova

head  of  the  chair  of  Physics  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

Natalia  Andreeva

associate  professor  of  the  chair  of  Physics  of  branch  of  Military  Diplomatic  Academy  of  the  Ministry  of  Defence,  Russia  Cherepovets

АННОТАЦИЯ

Рассчитываются  некоторые  физические  характеристики  и  параметры  изотропного  оптического  излучателя  в  однородной  безграничной  диэлектрической  и  проводящей  средах,  в  частности  амплитуда  напряженности  электрического  поля  направленной  антенны.  Исследована  зависимость  диэлектрической  проницаемости  от  частоты  колебания  внешнего  поля.  Рассчитана  глубина  проникновения  волны  в  среду.

ABSTRACT

There  are  calculated  some  physical  characteristics  and  parameters  of  an  isotropic  optical  radiator  in  homogeneous  unbounded  dielectric  and  conducting  mediums,  namely  the  amplitude  of  electric  field  intensity  of  a  guided  antenna.  The  dependence  of  capacitivity  from  vibration  frequency  of  external  field  has  been  studied.  The  depth  of  wave  penetration  into  medium  has  been  calculated. 

Ключевые  слова:  однородная  безграничная  среда,  изотропный  излучатель,  антенна,  свободное  пространство,  мощность  излучения

Keywords:  homogeneous  unbounded  medium;  isotropic  radiator;  antenna;  free  space;  radiated  power.

Однородная  безграничная  среда  может  представлять  собой  свободное  пространство,  диэлектрическую  среду,  среду  с  проводимостью,  а  также  среду  со  свободными  зарядами.

Свободное  пространство  представляет  собой  безграничную  среду,  у  которой  диэлектрическая  и  магнитная  проницаемость  равны  единице,  удельная  проводимость  равна  нулю,  поглощение  в  среде  отсутствует.  Реально  таких  сред  не  существует,  однако,  выражения,  описывающие  условия  распространения  электромагнитных  волн,  являются  фундаментальными.  Распространение  электромагнитных  волн  в  более  сложных  случаях  характеризуется  теми  же  выражениями  с  внесением  в  них  определенных  поправок.

Пусть  источником  электромагнитных  волн  является  изотропный  излучатель,  т.  е.  антенна,  излучающая  одинаково  во  всех  направления.  Реальные  антенны  излучают  неизотропно,  но  направленность  реальных  антенн  можно  учесть  с  помощью  так  называемого  коэффициента  направленного  действия  (КНД)  D.  Под  КНД  антенны  понимается  число,  представляющее  отношение  квадрата  модуля  напряженности  электрического  поля,  создаваемого  антенной  в  направлении  максимального  излучения,  к  среднему  (по  всем  направлениям)  значению  квадрата  напряженности  этого  поля

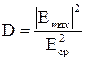.                                                 (1)

Например,  элементарный  диполь  —  это  слабо  направленная  антенна  с  КНД  1,5.  Как  известно,  характеристикой  движения  энергии  в  волне  является  вектор  Пойнтинга  ,  где  ,  .

Среднее  значение  этого  вектора

.                                              (2)

На  расстоянии  r  от  излучателя  мощность  излучения  равна

.                      (3)

Учитывая,  что  в  электромагнитной  волне  в  любой  момент  времени  плотности  энергии  электрического  и  магнитного  полей  равны  ,  найдем  связь  между  амплитудными  значениями    и  :

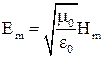.                                              (4)

Подставив  в  (4)  значения  электрической  и  магнитной  постоянных,  получим    —  волновое  сопротивление  свободного  пространства.

Тогда 

.                                                (5)

Выразим  из  (5)  значение  ,  подставим  его  в  (2)

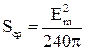,                                                 (6)

или,  из  (3)  получим

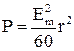,                                                   (7)

Откуда

.                                                (8)

С  учетом  КНД  получаем,  что  амплитуда  напряженности  электрического  поля  направленной  антенны  равна

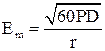.                                              (9)

Выражение  (9)  справедливо  для  антенн  любого  типа,  если  поставить  в  него  соответствующее  значение  коэффициента  направленного  действия  D.

Примером  свободного  пространства  может  быть  космическое  пространство  в  пределах  Солнечной  системы.  Концентрация  частиц  на  таких  расстояниях  ()  не  изменяет  существенно  его  свойства.  В  то  же  время  межзвездное  пространство,  имеющее  концентрацию  атомов  и  молекул  на  порядок  меньше,  не  может  оставаться  свободным  ввиду  больших  расстояний,  которые  проходят  электромагнитные  волны  и,  следовательно,  взаимодействуют  с  большим  количеством  вещества.

I.    Пусть  электромагнитные  волны  распространяются  в  безграничной  среде,  характеризуемой  ,    и  .  Связь  этих  характеристик  дается  соотношениями:

;               ;            .                        (10)

Запишем  уравнения  Максвелла  в  дифференциальной  форме

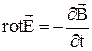,                                       (11)

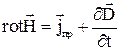.                                           (12)

Уравнения  электромагнитной  волны  для  компонент    и    запишутся

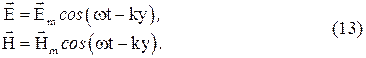
В  комплексной  форме  (13)  выглядят  следующим  образом:

,

где:    —  комплексная  амплитуда  колебаний  вектора    в  электромагнитной  волне.

Аналогично,  для  вектора 

,

где:    —  комплексная  амплитуда  колебаний  вектора    в  электромагнитной  волне.

Плотность  тока  проводимости  по  закону  Ома  равна  .  С  учетом  вышеизложенного  уравнения  (11)  будет

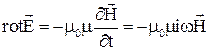.                         (14)

Аналогично,  уравнение  (12)

.                              (15)

Таким  образом,  в  правой  части  (15)  находится  вектор,  состоящий  из  двух  частей.  Для  того  чтобы  записать  (15)  формально  аналогично  (14),  введем  так  называемую  комплексную  диэлектрическую  проницаемость.

             (16)

,                                      (17)

где:    —  комплексная  диэлектрическая  проницаемость  среды.

Если  ,  то  ,  т.  е.  среда  является  чисто  диэлектрической.  При  прохождении  электромагнитной  волны  через  диэлектрик  происходит  взаимодействие  электрической  и  магнитной  компонент    и    с  электронами,  входящими  в  состав  молекул  (атомов)  вещества.  Такие  электроны  начинают  колебаться  с  частотой  вынуждающей  силы,  т.  е.  с  частотой    электромагнитного  поля.

Рисунок  1.  Зависимость  амплитуды  колебаний  от  частоты  электромагнитного  поля

Амплитуда  колебаний  зависит  от  соотношения  между    и  ,  где    —  собственная  частота  электронного  осциллятора  (рис.  1).  В  результате  диэлектрическая  проницаемость  среды  становится  функцией  частоты  .  Поскольку,  согласно  теории  Максвелла 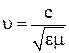 ,  то  это  означает,  что  и    тоже  зависит  от  частоты  колебаний  внешнего  электромагнитного  поля  .  Показатель  преломления  данной  волны  оказывается  зависящим  от  частоты  падающего  света,  и  длина  волны  в  среде

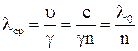,                                       (18)

где:    —  длина  волны  в  вакууме.

С  ростом  частоты  колебаний  внешнего  поля    диэлектрическая  проницаемость  уменьшается.  Это  объясняется  тем,  что  с  увеличением    молекулярные  диполи,  например,  полярные  молекулы  воды,  не  успевают  ориентироваться  в  направлении  электрического  поля.  Отметим,  что  при  распространении  электромагнитных  волн  разница  между  диспергирующими  средами  и  средами  без  дисперсии  имеет  смысл  лишь  в  отношении  немонохроматических  волн  ().

Распространение  волны  в  диэлектрике  описывается  уравнением

                         (19)

Для  диэлектрика  волновое  число  .

Тогда  комплексную  амплитуду  напряженности  электрического  поля  можно  представить

,                                            (20)

где:  y  —  расстояние,  пройденное  волной  в  данной  среде.

II. Пусть  волна  распространяется  в  проводящей  среде.

Рассмотрим,  как  меняется  уравнение  плоской  волны  в  среде  с  потерями,  где  .  Введение  комплексной  диэлектрической  проницаемости  среды  (17),  позволяет  получить  выводы,  относящиеся  к  распространению  волн  в  проводящей  среде  из  соответствующих  формул  для  диэлектрика  путем  замены  в  них  вещественной  диэлектрической  проницаемости  среды    на  комплексное  значение  диэлектрической  проницаемости  .  При  этом  квадрат  постоянной  распространения  (волнового  числа)  вместо  k  запишем  :

,

.             (21)

Постоянная  распространения

.                                  (22)

Так  как  корень  квадратный  из  комплексного  числа  напрямую  не  вычисляется,  сделаем  следующие  преобразования.

Запишем

.                                                   (23)

Здесь  k  —  действительная  часть  постоянной  распространения,  s  —  мнимая  часть.

Уравнение  (23)  возводим  в  квадрат  и  приравниваем  к  значению    из  (21):

   (24)

Приравнивая  действительные  и  мнимые  части  (24),  находим

Введя  обозначения  a  и  b,  решаем  систему  относительно    и  .

Из  (25)  находим  k:  ,  и  подставляем  в  (26) 

.

Возведем  в  квадрат  обе  части:

;     .         (27)

Получили  биквадратное  уравнение;  вводим  новую  переменную  ;  .  Тогда  , 

.

Решаем  полученное  уравнение:

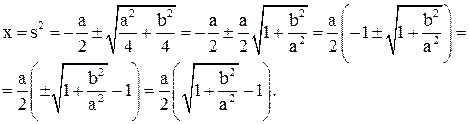           (28)

(  не  может  быть  отрицательным).

Подставляя  (28)  в  (25)  в  итоге  имеем

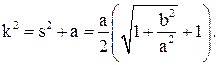       (29)

Найдем  .

Тогда

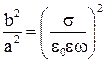,                                                       (30)

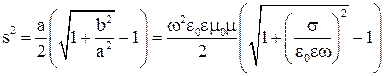,                           (31)

.                           (32)

С  учетом  полученных  выражений,  запишем  решение  волнового  уравнения  для  плоской  одномерной  волны,  распространяющейся  в  проводящей  среде  в  направлении  оси  oy.    представим  в  виде  (23):

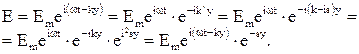               (33)

Экспонента    говорит  об  уменьшении  амплитуды    при  распространении  волны  в  среде.  На  пути  ,  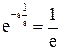  —  амплитуда  волны  затухает  в  e  раз.  Эта  величина  определяет  глубину  проникновения  волны  в  проводящую  среду.

Найдем  s  из  (31)

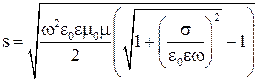.                        (34)

Для  всех  разумных  значений  частот    и  проводимостей    отношение  .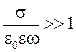 

Например,  для  морской  воды  ,  ,  ,  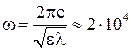;  тогда  .

Пренебрегая  единицами  в  (34),  получаем

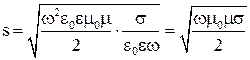.                          (35)

Глубина  проникновения,  на  которой  амплитуда  волны  уменьшается  в  e  раз,  равна

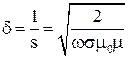.                                                  (36)

Таким  образом,  волна,  попав  в  проводящую  среду,  частично  или  полностью  поглощается  и  характеризует  поглощение  мнимая  часть  s  комплексного  коэффициента  распространения  ,  связанная  с  удельной  проводимостью.

Глубина  проникновения  волны  в  проводящую  среду  зависит  от  частоты  волны  и  проводимости  среды.  Например,  глубина  проникновения  световых  волн  в  металл  имеет  порядок  .  Энергия  волны  переходит  в  джоуль–ленцево  тепло.  В  средах  с  достаточной  проводимостью  для  целей  радиосвязи  следует  использовать  радиоволны  с  большей  длиной  волны.  Например,  связь  с  подводными  лодками,  находящимися  в  морской  воде,  осуществляется  на  длинах  волн  ,  если  удельная  проводимость  морской  воды  ,  то  из  (36)  следует,  что  .

Список  литературы:

1.Грудинская  Г.П.  Распространение  радиоволн:  Учеб.  пособие  для  вузов.  М.:  Высшая  школа,  1975. 

2.Марков  Г.Т.,  Петров  Б.В.,  Грудинская  Г.П.  Электродинамика  и  распространение  радиоволн:  Учеб.  пособие  для  вузов.  М.:  Сов.  радио,  1969.

3.Татур  Т.А  Основы  теории  электромагнитного  поля.  М.:  Высшая  школа,  1989.