Статья опубликована в рамках: XIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 09 декабря 2013 г.)
Наука: Физика
Секция: Акустика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛЬ АСИМПТОТИЧЕСКИ ОСРЕДНЕННОГО ТЕМПЕРАТУРНОГО ПОЛЯ ТУРБУЛЕНТНОГО ГАЗОВОГО ПОТОКА
Филиппов Александр Иванович
д-р техн. наук, профессор СФ БашГУ, РФ, Республика Башкортостан, г. Стерлитамак
E-mail: filippovai@rambler.ru
Ахметова Оксана Валентиновна
канд. физ.-мат. наук, доцент СФ УГНТУ, РФ, Республика Башкортостан, г. Салават
E-mail: ahoksana@yandex.ru
Олефиренко Константин Викторович
аспирант СФ БашГУ, РФ, Республика Башкортостан, г. Стерлитамак
MODEL IS ASYMPTOTICALLY AVERAGED TEMPERATURE FIELD OF TURBULENT GAS FLOW
Filippov Alexandr Ivanovich
doctor of engineering sciences, professor of Bashkir State University, Republik of Bashkortostan,
Sterlitamak
Akhmetova Oksana Valentinovna
candidate of phys.-mathem. sciences, associate professor of Ufa State Petroleum
Technological University, Republik of Bashkortostan, Salavat
Olefirenko Konstantin Viktorovich
aspirant of Bashkir State University, Republik of Bashkortostan, Sterlitamak
АННОТАЦИЯ
В работе представлены результаты расчетов температуры газового потока на основе выражений для нулевого коэффициента асимптотического разложения. Построенные зависимости позволяют судить о характере изменения температуры по стволу газовой скважины и во времени, что составляет основу интерпретации термограмм.
ABSTRACT
The paper presents the results of calculations of temperature gas stream based on the expressions for the zero coefficient of the asymptotic expansion. Built dependencies allow to judge the nature of temperature change on the trunk and gas well in time, that is the basis of the interpretation of infrared images.
Ключевые слова: поток газа; газовая скважина; температурное поле; асимптотический метод; турбулентный режим течения.
Keywords: gas flow; gas well; temperature field; asymptotic method; turbulent flow regime.
При исследовании температурного поля газового потока в скважине необходим учет сжимаемости среды. Уменьшение давления от пластового до атмосферного при течении газа в скважине приводит к изменению плотности среды на один-два порядка. Даже при стационарном течении плотность газа является функцией относительной вертикальной цилиндрической координаты ![]() :
: ![]() .
.
Оценки показывают, что радиальной координатой скорости vr в сравнении с вертикальной v можно пренебречь. Из стационарного уравнения неразрывности ![]() следует, что произведение плотности на скорость остается постоянным на поверхности фиксированного радиуса и равным произведению плотности
следует, что произведение плотности на скорость остается постоянным на поверхности фиксированного радиуса и равным произведению плотности ![]() и скорости
и скорости ![]() при некотором заданном значении
при некотором заданном значении ![]() :
: ![]() .
.
Математическая постановка задачи о температурном поле газовой скважины включает уравнение теплопроводности в окружающем трубу массиве
|
|
(1) |
и уравнение конвективной теплопроводности потока газа в скважине
|
|
(2) |
Выражение для плотности источников ![]() учитывает переход механической энергии в теплоту (за счет трения) и адиабатический эффект в восходящем потоке газа и другие источники тепла.
учитывает переход механической энергии в теплоту (за счет трения) и адиабатический эффект в восходящем потоке газа и другие источники тепла.
Условия на границе трубы и окружающего массива определяются равенством температур
|
|
(3) |
и тепловых потоков
|
|
(4) |
Начальные условия соответствуют естественной невозмущенной температуре Земли, возрастающей с глубиной ![]() по линейному закону
по линейному закону
|
|
(5) |
которая совпадает с температурой в удаленных от трубы точках окружающего массива
|
|
(6) |
В точке ![]() температура потока изменяется заданным образом и зависит от времени
температура потока изменяется заданным образом и зависит от времени
|
|
(7) |
В задаче (1)—(7) переменные коэффициенты R(rd /r0) и l(rd /r0) представляют зависимость скорости и коэффициента теплопроводности от радиальной координаты, а Z(zd /D) — зависимость плотности от вертикальной координаты. В предлагаемых расчетах эти коэффициенты определены из уравнений Сполдинга [1] и уравнения состояния Менделеева-Клапейрона.
С использованием соотношений
|
|
задача (2.1)—(2.7) приводится к безразмерным переменным. При этом в уравнениях (2.1) и (2.2) слагаемые, содержащие вторую производную температуры по вертикальной координате, приобретают малый множитель — квадрат величины ![]() ~ 10–4, где
~ 10–4, где ![]() ~ 0,1 м — радиус скважины и D ~ 103 м — ее длина. Поэтому слагаемые, содержащие коэффициент
~ 0,1 м — радиус скважины и D ~ 103 м — ее длина. Поэтому слагаемые, содержащие коэффициент ![]() в уравнениях, опущены.
в уравнениях, опущены.
С учетом вышесказанного в безразмерном виде задача (2.1)—(2.7) запишется как
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
В задаче (2.8)—(2.14) заменой ![]() на
на ![]() формально введен параметр асимптотического разложения . Такое введение формального параметра в задаче имеет физический смысл, заключающийся в том, что устремление его к нулю
формально введен параметр асимптотического разложения . Такое введение формального параметра в задаче имеет физический смысл, заключающийся в том, что устремление его к нулю ![]() соответствует возрастанию радиальной компоненты теплопроводности газа до бесконечности
соответствует возрастанию радиальной компоненты теплопроводности газа до бесконечности ![]() (случай =1 соответствует исходной задаче). Задача (2.8)—(2.14) представляет собой задачу сопряжения, содержащую краевые условия 4-го рода и линейное неоднородное дифференциальное уравнение параболического типа с тремя переменными коэффициентами
(случай =1 соответствует исходной задаче). Задача (2.8)—(2.14) представляет собой задачу сопряжения, содержащую краевые условия 4-го рода и линейное неоднородное дифференциальное уравнение параболического типа с тремя переменными коэффициентами ![]() и стационарным источником
и стационарным источником![]() . Решение задачи о температурном поле турбулентного потока газа в скважине, содержащей уравнения с переменными коэффициентами, найдено на основе развитой авторами модификации асимптотического метода в форме
. Решение задачи о температурном поле турбулентного потока газа в скважине, содержащей уравнения с переменными коэффициентами, найдено на основе развитой авторами модификации асимптотического метода в форме
|
|
(15) |
Величина остаточного члена ![]() дает оценку точности нулевого приближения. Для
дает оценку точности нулевого приближения. Для ![]() формулируется краевая задача и отыскивается точное или приближенное решение. Исследование поведения найденного решения для остаточного члена позволяет отыскать область лучшей применимости первого приближения.
формулируется краевая задача и отыскивается точное или приближенное решение. Исследование поведения найденного решения для остаточного члена позволяет отыскать область лучшей применимости первого приближения.
Далее показано, что коэффициент ![]() может быть найден таким образом, что асимптотически осредненное значение остаточного члена обращается в нуль
может быть найден таким образом, что асимптотически осредненное значение остаточного члена обращается в нуль ![]() при любых значениях параметра e. Такое асимптотическое приближение соответствует «в среднем точному».
при любых значениях параметра e. Такое асимптотическое приближение соответствует «в среднем точному».
Выражение для нулевого коэффициента разложения температуры флюида имеет вид
|
|
(16) |
где 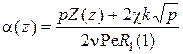 ,
,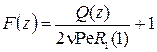 . Для внешней области
. Для внешней области
|
|
(17) |
Выражения (16) и (17) представляют точное решение задачи в нулевом приближении в пространстве изображений.
В предположении малых времен в пространстве оригиналов (16) представится как
|
|
(18) |
Формула (18) позволяет строить пространственно-временные зависимости асимптотически осредненной по радиусу температуры турбулентного потока газа.
Для расчета кривых использованы следующие значения параметров скважины: D = 1000 м, r0 = 0,031 м; наполняющего флюида: метан с = 2866 Дж/(К×кг), r = 71,4 кг/м3; окружающей среды: G = 0,04 K/м, глина — l = 0,67 Вт/(м×К), с = 950 Дж/(К×кг), r = 2000 Дж/(К×кг). Безразмерный температурный сигнал пласта T0 = -1.
Рис. 1 иллюстрирует зависимость температуры метана при дебите Qm = 100 т/сут от безразмерной вертикальной координаты при разных значениях безразмерного времени.
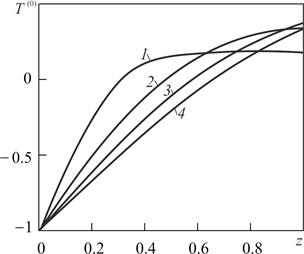
Рисунок 1. Зависимость температуры от вертикальной координаты для различных значений безразмерного времени: 1 — Fo = 0,22, 2 — 0,44, 3 — 0,66, 4 — 0,88
На рис. 2 представлена зависимость температуры от вертикальной координаты для различных значений параметра Пекле
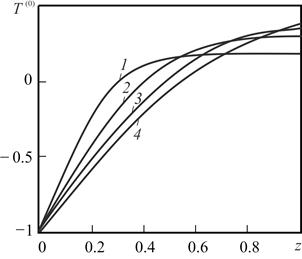
Рисунок 2. Зависимость температуры от вертикальной координаты для различных значений параметра Пекле: 1 — Pe = 14,7, 2 — 22,85, 3 — 30,47, 4 — 38,09
На рис. 3 представлена зависимость температуры газа от безразмерного времени при разных значениях безразмерной вертикальной координаты.

Рисунок 3. Зависимость температуры газа от безразмерного времени при разных значениях безразмерной вертикальной координаты: 1 — z = 0,9, 2 — 0,7, 3 — 0,5, 4 — 0,3
Зависимость температуры от безразмерного времени для различных значений параметра Пекле показана на рис. 4.

Рисунок 4. Зависимость температуры от безразмерного времени для различных значений параметра Пекле: 1 — Pe = 14,7, 2 — 22,85, 3 — 30,47, 4 — 38,085
Итак, применение метода асимптотического разложения по формальному параметру позволило построить приближенное аналитическое решение задачи о температурном поле газовой скважины, содержащей уравнение сопряжения с тремя переменными коэффициентами.
Анализ полученных результатов показывает, что полученные выражения для температуры удовлетворяют большинству требований, предъявляемых к инженерным методам расчетов, и могут быть широко использованы на практике.
Список литературы:
1.Филиппов А.И., Ахметова О.В., Родионов А.С. Температурное поле турбулентного потока в скважине // Теплофизика высоких температур. — 2013. — Т. 51, — № 2. — С. 277—286.
2.Филиппов А.И., Ахметова О.В., Родионов А.С. Асимптотическое осреднение температуры турбулентного потока в скважине. // Вестник Тюменского государственного университета. — 2012, — № 4. — С. 6—13.
дипломов


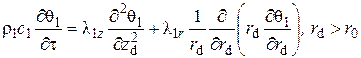 ,
, 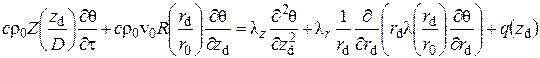 ,
, 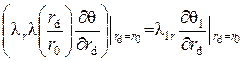 .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,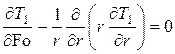 ,
, 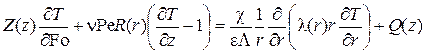 ,
,  ,
,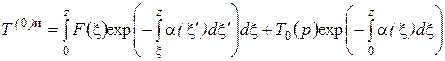 , , ,
, , , ,
, 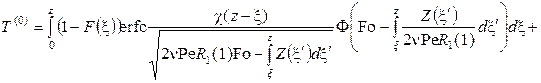
 , , .
, , .
Оставить комментарий