ОСОБЕННОСТИ  ТРАНСЗВУКОВОГО  ОБТЕКАНИЯ  АЭРОДИНАМИЧЕСКОГО  ПРОФИЛЯ  ПРИ  ОТКЛОНЕНИИ  ЭЛЕРОНА

Бабарыкин  Константин  Валентинович

канд.  физ.-мат.  наук,  научный  сотрудник,  Санкт-Петербургский  государственный  университет,  РФ,  г.  Санкт-Петербург

E-mail: 

CHARACTERISTICS  OF  TRANSONIC  FLOWING  PAST  AIRFOILE  WITH  DEFLECTED  AILERON

Babarykin  Konstantin  Valentinovich

philosophy  doctor,  researcher  ,  Saint-Petersburg  State  University,  Russia  Saint-Petersburg

Работа  выполнена  при  поддержке  РФФИ  (проект  №  13-08-00288)

Исследования  были  проведены  с  использованием  вычислительных  ресурсов  Ресурсного  Центра  "Вычислительный  центр  СПбГУ"  (http://cc.spbu.ru)

АННОТАЦИЯ

Проведено  численное  исследование  трансзвукового  обтекания  профиля  Whitcomb  известной  CFD-программой  Fluent.  Изучено  поведение  коэффициента  подъемной  силы  в  диапазоне  числа  Маха  от  0.81  до  0.86.  Проведено  сравнение  полученных  результатов  с  данными  аналогичных  расчетов  другой  программой.  Изучено  аномально  резкое  уменьшение  коэффициента  подъемной  силы  при  сравнительно  небольшом  поднятии  элерона  для  числа  Маха  0.82.

ABSTRACT

A  numerical  investigation  of  transonic  flow  around  airfoil  Whitcomb  by  well  known  CFD  program  Fluent  is  carried  out.  The  behavior  of  lift  coefficient  in  the  range  of  freestream  Mach  number  from  0.81  to  0.86  is  considered.  The  obtained  results  are  compared  with  the  data  of  similar  calculations  by  another  program.  An  abnormally  sharp  reduction  of  the  lift  coefficient  with  a  relatively  small  aileron  raising  for  freestream  Mach  number  0.82  is  studied.

Ключевые  слова:  трансзвуковое  течение;  аэродинамический  профиль;  коэффициент  подъемной  силы;  ударная  волна. 

Keywords:  transonic  flow;  airfoil;  lift  coefficient;  shock  wave.

Введение.  Постановка  задачи.

В  настоящей  работе  рассматривается  трансзвуковое  обтекание  несимметричного  аэродинамического  профиля  Whitcomb.  Его  форма  представлена  на  рис.  1.  Длина  профиля  2,5  м,  толщина  составляет  11,5  %  от  длины  хорды,  в  хвостовой  части  имеется  элерон,  длина  которого  составляет  30  %  от  общей  длины.

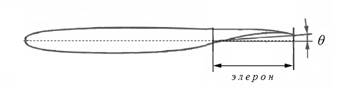
Рисунок  1.

Данный  профиль  имеет  высокие  аэродинамические  характеристики  при  числах  Маха  набегающего  потока  до  0,8,  однако  их  поведение  при  M_∞  >  0,81  изучено  недостаточно.  В  [1—2]  обнаружены  условия  обтекания,  при  которых  происходит  резкое  изменение  коэффициента  подъемной  силы,  обусловленное  расщеплением  или  слиянием  местных  сверхзвуковых  зон  на  верхней  стороне  профиля.  Также  выявлено,  что  при  числе  Маха,  превышающем  0,85,  течение  практически  невосприимчиво  к  отклонению  элерона  от  нейтрального  положения,  что  может  затруднить  управление  трансзвуковым  обтеканием.  Таким  образом,  целью  настоящей  работы  является  изучение  течения  около  профиля  в  диапазоне  чисел  Маха  от  0,81  до  0,86.

Моделировалось  турбулентное  обтекание  профиля  потоком  газа  со  следующими  параметрами:  давление  p_∞  =  26434  Па,  температура  T_∞  =  223,15  K,  что  соответствует  параметрам  атмосферы  на  высоте  10  км.  Расчеты  проводились  по  программе  ANSYS  Fluent  13  на  различных  сетках,  содержащих  от  227  до  600  тыс.  элементов 

Результаты  предварительных  расчетов

Был  проведен  ряд  тестовых  расчетов  на  режиме  M_∞  =  0,8485  и  углом  атаки  α  от  -1°  до  1°,  с  отклонением  элерона  θ  =  4°,  в  которых  были  опробованы  различные  модели  турбулентности,  как  классическая  модель  Spalart-Allmaras,  так  и  более  современные  модели  SST.  Эти  расчеты  показали,  что  модели  SST  Transition  и  SST  k-ω  дают  довольно  близкие  значения  коэффициента  подъемной  силы  C_L.  Значения  C_L,  полученные  при  использовании  модели  Spalart-Allmaras  довольно  заметно  отличаются  в  большую  сторону.  Это,  в  общем,  подтверждает  факт,  что  модель  турбулентности  Spalart-Allmaras  в  случае  трансзвукового  обтекания  аэродинамического  профиля  может  давать  худшие  по  сравнению  с  моделями  семейства  SST  результаты.  Основная  часть  расчетов  поэтому  велась  с  использованием  хорошо  себя  зарекомендовавшей  в  этом  круге  задач  модели  SST  κ-ω  [3].  Эта  модель  довольно  точно  описывает  течения  с  отрывом  турбулентного  погранслое  от  гладких  поверхностей.  

Для  верификации  вычислительной  программы  некоторые  режимы  обтекания  были  просчитаны  на  разных  сетках,  227  и  387  тыс.  элементов.  Было  обнаружено,  что  результаты  расчетов  практически  не  восприимчивы  к  сгущению  сетки.  Так,  на  режиме  M_∞  =  0.8485  ,  α  =  0°,  с  отклонением  элерона  θ=4°,  при  переходе  к  более  густой  сетке  изменение  C_L  составило  примерно  6  %.  Аналогичные  результаты  были  получены  для  режимов  с  отклонением  элерона  4  и  5°  для  M_∞  =  0,82.  Для  меньших  отклонений  элерона  (1,3°),  результаты  оказались  более  чувствительны  к  сетке.  В  целом  же  можно  сделать  вывод,  что  для  рассматриваемого  профиля  дальнейшее  сгущение  сетки  практически  не  влияет  на  C_L. 

Исследование  зависимости  C_L  от  числа  Маха  и  геометрии  профиля

Было  исследовано  влияние  числа  Маха  набегающего  потока  на  коэффициент  подъемной  силы.  Рассчитывались  режимы  с  нулевым  углом  атаки  и  нулевым  отклонением  элерона,  число  Маха  менялось  от  0,81  до  0,86.  Расчет  показал,  что  при  увеличении  числа  Маха  происходит  значительное  уменьшение  аэродинамического  качества  профиля.  Для  числа  Маха  0,81  значение  C_L  составило  ≈  0,49  (что  неплохо  отвечает  экспериментальному  ≈  0,53  [4]),  при  увеличении  M_∞  наблюдается  уменьшение  коэффициента  подъемной  силы  почти  в  10  раз  при  M_∞  =0,86.  Зависимость  коэффициента  подъемной  силы  C_L  от  числа  Маха  M_∞  представлена  на  рис.  2.  Данный  результат  получен  на  сетке  в  227  тыс.  ячеек,  при  этом  использовался  реализованный  в  Fluent  алгоритм  density-based.  Для  сравнения  на  этом  же  рисунке  приведены  данные,  полученные  расчетом  программой  CFX.  Можно  отметить  хорошее  качественное  и  количественное  согласование  данных,  полученных  разными  программами. 

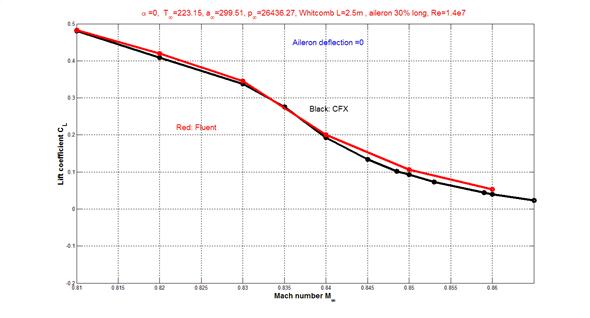
Рисунок  2.

Резкое  уменьшение  подъемной  силы  при  увеличении  числа  Маха  можно  объяснить  следующим  образом.  Известно,  что  при  трансзвуковом  обтекании  на  верхней  и  нижней  сторонах  профиля  могут  образовываться  местные  сверхзвуковые  области,  при  определенных  условиях  с  замыкающей  ударной  волной.  Коэффициент  подъемной  силы  зависит  от  соотношения  размеров  этих  зон.  Особенность  рассматриваемого  профиля  заключается  в  том,  что  при  сравнительно  небольших  числах  Маха  на  нижней  поверхности  профиля  не  образуется  ярко  выраженной  сверхзвуковой  зоны,  что  и  обеспечивает  высокие  значения  C_L.  Проведенный  расчет  также  показал,  что  на  малых  числах  Маха  формируются  лишь  небольшие  сверхзвуковые  области  (рис.  3а).  На  верхней  стороне  профиля  в  исследованном  диапазоне  M_∞  образуется  одна  большая  сверхзвуковая  зона,  размеры  которой  при  изменении  M_∞  меняются  незначительно.  На  нижней  же  стороне  картина  течения  претерпевает  существенную  перестройку.  При  больших  значениях  M_∞  формируется  классическая  сверхзвуковая  зона  с  замыкающей  ударной  волной  (рис.  3б).  Увеличение  M_∞  приводит  к  увеличению  размеров  этой  зоны.  Соответственно,  суммарная  сила,  действующая  на  нижнюю  часть  профиля,  также  уменьшается.  При  этом  сила,  действующая  на  верхнюю  поверхность,  меняется  мало,  вследствие  чего  и  происходит  наблюдаемое  в  диапазоне  числа  Маха  от  0,81  до  0,86  падение  C_L.

Рисунок  3.  а  —  Поля  числа  Маха,  M_∞  =  0,82;  б  —  Поля  числа  Маха,  M_∞  =  0,85

Важной  характеристикой  аэродинамического  профиля  или  крыла  является  его  управляемость.  Поэтому  существенным  моментом  является  реакция  картины  обтекания  на  изменение  положения  управляющих  элементов.  В  нашем  случае  интерес  представляет  поведение  подъемной  силы  при  поднятии  или  опускании  элерона.  При  расчетах  программой  CFX  было  обнаружено,  что  при  сравнительно  малых  числах  Маха,  до  0,83,  может  происходить  сильное  изменение  коэффициента  подъемной  силы  при  малом  изменении  угла  отклонения  элерона  θ  от  нейтрального  положения.  Было  проведено  численное  исследование  течения  при  M_∞  =  0,82  и  отклонении  элерона  от  0  до  5°.  В  этой  серии  расчетов  использовался  алгоритм  pressure-based,  количество  элементов  сетки  было  большим,  порядка  387  тыс.  На  рис.  4  приведены  графики  зависимости  C_L  от  θ  для  углов  атаки  α  =  0°  и  α  =  0.4°.  Также  для  нулевого  угла  атаки  приведена  зависимость,  полученная  в  CFX. 

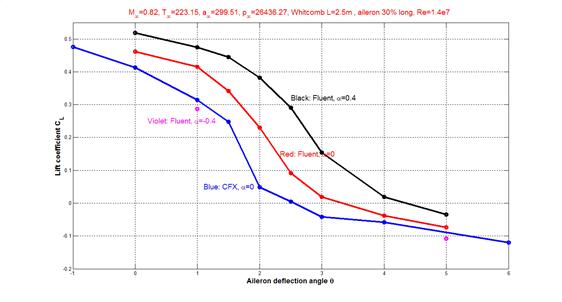
Рисунок  4.

Как  показали  расчеты,  и  в  CFX,  и  во  Fluent,  самое  резкое  падение  C_L  происходит  при  увеличении  θ  от  1°  до  3°.  Видно,  что  при  сохранении  общей  тенденции  к  уменьшению  C_L  количественные  расхождения  в  результатах  разных  программ  отмечаются  именно  на  этом  участке.  Были  проведены  также  расчеты  для  отрицательного  угла  атаки  при  θ  =  1°  и  θ  =  5°.  Было  обнаружено,  что  при  α  =  –0.4°  перепад  C_L  заметно  меньше,  чем  нулевом  угле.  При  положительном  же  угле  атаки,  как  следует  из  полученной  зависимости  для  α  =  0,4°,  данный  эффект  проявляется  сильнее.  Рассмотрим  эволюцию  картины  течения,  наблюдающуюся  при  нулевом  угле  атаки  вследствие  увеличения  отклонения  элерона  θ.  На  рис.  4а—4г  приведены  результаты  расчета  для  различных  значений  θ.  При  нулевом  угле  отклонения  газ  над  профилем  обтекает  гладкую  поверхность,  при  поднятии  элерона  на  верхней  поверхности  появляется  точка  излома.  По  сути,  сверхзвуковой  поток  в  верхней  зоне  обтекает  внутренний  тупой  угол.

Рисунок  4.  а)  Поля  числа  Маха,  θ  =  1,5°;  б)  Поля  числа  Маха,  θ  =  2,0°;  в)  Поля  числа  Маха,  θ  =  2,5°;  г)  Поля  числа  Маха,  θ  =  3,0

Из  теории  ударных  волн  известно,  что  возможен  разворот  потока  в  таком  угле  на  косой  ударной  волне  с  сохранением  сверхзвуковой  скорости.  В  нашем  случае  при  выходе  слабой  косой  волны  на  замыкающую  ударную  волну  образуется  λ-конфигурация  ударных  волн.  Так  как  газ  в  сверхзвуковой  зоне  разгоняется  до  сравнительно  малых  чисел  Маха  (≈  1,3),  то  какой  характер  обтекания  точки  излома  может  наблюдаться  лишь  при  очень  малых  θ.  При  дальнейшем  увеличении  θ  разворот  потока  в  присоединенной  ударной  волне  становится  невозможен,  и  газ  начинает  тормозиться  на  отошедшей  ударной  волне.  Кроме  того,  по  мере  увеличения  θ  увеличивается  и  расстояние  от  ударной  волны  до  точки  излома.  Аналогичная  картина  имеет  место  в  случае  обтекания  тел  плохой  аэродинамической  формы  сверхзвуковым  потоком,  когда  головная  ударная  волна  располагается  от  тела  тем  дальше,  чем  более  оно  затуплено,  а  также  чем  меньше  число  Маха  набегающего  потока.  Поэтому  на  рис.  4в  и  4г  мы  видим  лишь  небольшую  сверхзвуковую  зону  на  верхней  части  профиля.  Не  менее  существенные  изменения  наблюдаются  и  на  нижней  стороне  профиля.  При  поднятии  элерона  газ  вдоль  нижней  поверхности  начинает  течь  более  свободно,  что  позволяет  ему  разгоняться  до  больших  значений  числа  Маха.  Если  при  нулевом  или  небольшом  значении  θ  присутствуют  лишь  небольшие  сверхзвуковые  области,  как  на  рис.  4а,  то  при  θ  ≥  2°  уже  формируется  полноценная  сверхзвуковая  область  с  замыкающей  ударной  волной.  На  участке  разгона  газа  давление  снижается  сильнее,  а  сам  участок  становится  протяженнее.  При  дальнейшем  увеличении  θ  растут  размеры  сверхзвуковой  зоны,  усиливается  и  замыкающая  волна,  а  точка  отрыва  погранслоя  смещается  вверх  по  течению.  Поток  перестает  попадать  на  поверхность  в  хвостовой  части  профиля,  под  элероном  образуется  зона  отрыва,  что  можно  заметить  при  сравнении  картины  течения  вблизи  хвоста  на  рис.  4а  и  рис.  4г.  Таким  образом,  при  увеличении  угла  элерона  на  небольшую,  в  2°,  величину,  происходит  резкая  перестройка  картины  течения  на  обеих  сторонах  профиля.  Одновременно  увеличивается  сила,  действующая  на  верхнюю  поверхность  профиля,  и  уменьшается  действующая  на  нижнюю.  Вследствие  этого  и  наблюдается  столь  резкое  падение  коэффициента  подъемной  силы. 

Заключение

Проведено  численное  исследование  трансзвукового  турбулентного  обтекания  профиля  Whitcomb  известной  CFD-программой  Fluent.  Осуществлен  ряд  тестовых  расчетов  на  различных  сетках,  с  использованием  различных  моделей  турбулентности.  Для  нулевого  угла  атаки  исследовано  поведение  коэффициента  подъемной  силы  C_L  в  диапазоне  числа  Маха  от  0,81  до  0,86.  Верификация  результатов  осуществлена  сравнением  полученных  данных  с  данными  аналогичных  расчетов  другой  программой.  Изучено  аномально  резкое  изменение  C_L  при  сравнительно  небольшом  изменении  геометрии  профиля.

Список  литературы:

1.Kuzmin  A.,  Ryabinin  A.  Airfoils  admitting  anomalous  behavior  of  lift  coefficient  in  descending  transonic  flight:  The  Seventh  Intern.  Conference  on  Comput.  Fluid  Dynamics,  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.iccfd.org/iccfd7,  —  2012,  —  pp.  1—7.

2.Kuzmin  A.  Transonic  flow  past  a  Whitcomb  airfoil  with  a  deflected  aileron  //  International  Journal  of  Aeronautical  and  Space  Sciences  —  2013.  —  Vol.  14  —  №  3  —  pp.  210—214.

3.Menter  F.R.  Review  of  the  Shear-Stress  Transport  turbulence  model  experience  from  an  industrial  perspective  //  Intern.  J.  Comput.  Fluid  Dynamics,  —  2009,  —  vol.  23,  Issue  4,  —  pp.  305—316.

4.Harris  C.D.  NASA  supercritical  airfoils:  NASA  Tech.  Paper  —  №  2969.  —  1990.  —  72  p.