ИДЕНТИФИКАЦИЯ  МНОГОМЕРНОЙ  НЕЛИНЕЙНОЙ  СТАЦИОНАРНОЙ  ДИНАМИЧЕСКОЙ  СИСТЕМЫ  ПРИ  НАЛИЧИИ  АВТОКОРРЕЛИРОВАННЫХ  ПОМЕХ  В  ВЫХОДНЫХ  СИГНАЛАХ

Руднев  Кирилл  Константинович

аспирант,  Самарский  государственный  университет  путей  сообщения,  РФ,  г.  Самара

E-mail: 

IDENTIFICATION  OF  MULTI-DIMENSIONAL  NON-LINEAR  STATIONARY  DYNAMIC  SYSTEM  IN  THE  PRESENCE  OF  AUTOCORRELATED  NOISES  IN  OUTPUT  SIGNALS

Rudnev  Kirill  Konstantinovich

candidate,  Samara  State  Transport  University,  Russia  Samara  city

аннотация

В  статье  предложен  численный  метод  оценивания  параметров  нелинейных  динамических  систем,  описываемых  разностными  уравнениями  при  наличии  помех  наблюдения  в  выходных  сигналах.

Abstract

There  is  numerical  method  of  estimation  of  parameters  of  multi-dimensional  non-linear  dynamic  system,  classified  difference  equations  in  the  presences  inquiry  interference  in  output  signals.

Ключевые  слова:  идентификация;  нелинейная  динамическая  система;  состоятельная  оценка.

Keywords:  identification;  non-linear  dynamic  system;  consistent  estimate.

Для  решения  многих  задач  на  железнодорожном  транспорте,  например,  таких  как  прогнозирование  расхода  электро­энергии,  контроль  функционального  состояния  машинистов,  прогнозирование  геометриче­ских  параметров  рельсовой  колеи,  прогнозирование  расхода  топлива  и  т.  д.,  применяются  модели  на  основе  разностных  уравнений.  Многие  из  этих  задач  нелинейные,  в  связи  с  чем  воз­никает  задача  построения  математических  моделей  на  основе  нелинейных  разностных  урав­нений.

Рассмотрим  многомерную  стационарную  нелинейную  динамическую  систему  с  дискретным  време­нем  ,  описываемую  следующим  уравнением:

  ,                                                                                    (1)

где    ;  =  ,,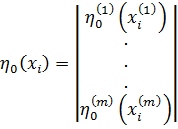

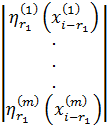где:    —  наблюдаемые  и  ненаблюдаемые  векторы  выходных  сигналов,

(,  є),  наблюдаемые  векторы  входных  сигналов  (є).

Идентификация  объекта  сводится  к  процедуре  определения  матриц  неизвестных  параметров    по  {,  }  при  известных  порядках    и  и  является  задачей  параметрического  оценивания.

В  общем  случае,  последовательность    не  является  последовательностью  независимых  случайных  векторов,  поэтому  представляет  интерес  случай  аддитивных  локальных  автокоррелированных  шумов  в  качестве  наблюдений.

Пусть  выполняются  следующие  условия:

1⁰.  Множество,  которому  априорно  при­надлежат  истинные  значения  параметров  ус­тойчивой  нелинейной  многомерной  системы,  является  компактом.

2°.    не  зависят  от  .

3⁰.  Случайные  последовательности  удовлетворяют  условиям:

E()  =  0  п.н.;

E(=  D>0

;

E(,

где:  —  случайная  матрица, 

  —  матрица  локальных  автокоррелированных  функций; 

4⁰.  Вектор  входных  сигналов  и  векторы  ,  …    и  истинные  параметры  удовлетворяют  условию:

,

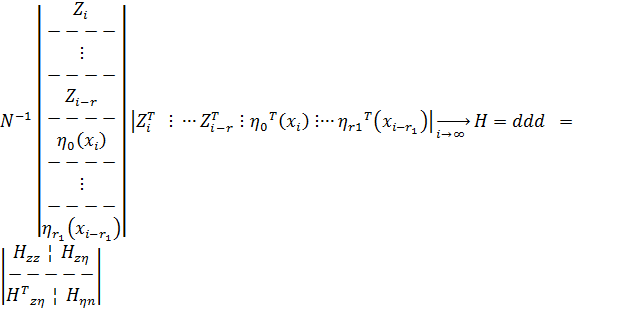где:  H  —  положительно  определенная  матрица.

5⁰.  Пусть  ,

,

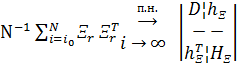где  :  имеет  размерность 

:  ,  где    —  положительно  определенные  матрицы,  элементы  которых    являются  значениями  локальной  автокоррелированной  функции  в  различные  моменты  времени.

Уравнение  (1)  можно  записать  в  виде:

  или               (2)

Представляем  уравнение  (2)  в  виде  системы  уравнений  (2)  :

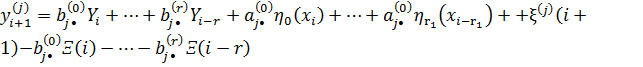                                                 (3)

где  j  строка  матриц  j  строка  матриц  ;

Уравнение  (3)  запишем  следующим  образом:

;

где  ,  ,

,  =

Введем  следующую  обобщенную  ошибку  для  j-уравнения:

;

Из  условий    и    следует,  что  обобщенная  ошибка  имеет  нулевое  среднее,  а  ее  локальная  дисперсия  с  вероятностью  1  равно:

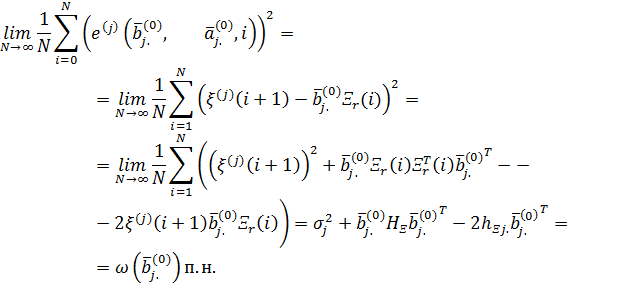
Определим  оценки    неизвестных  истинных  значений  параметров    из  условия  минимума  суммы  взвешенных  квадратичных  отклонений    с  весом  :

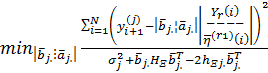                        (4)

Справедливо  следующее  утверждение:

Пусть  стационарная  нелинейная  динамическая  система  с  нулевыми  начальными  условиями  описывается  уравнением  (1)  и  помехи  удовлетворяют  условиям  .  Кроме  того,  истинные  значения  параметров    и  входные  сигналы  удовлетворяют  условиям  .  Тогда  оценка  определяемая  выражением  (4)  при    существует  и  является  сильно  состоятельной  оценкой,  т.е.  .

На  основе  данной  статьи  было  создано  прикладное  программное  обеспечение,  которое  позволит  получать  состоятельные  оценки  моделей  и  прогноза  потребления  энергоресурсов  на  железной  дороге.

Список  литературы:

1.Кацюба  О.А.,  Жданов  А.И.  Идентификация  по  методу  наименьших  квадратов  параметров  уравнений  авторегрессии  при  аддитивных  ошибках  измерений  //  Автоматика  и  телемеханика.  —  1982.  —  №  2.  —  с.  29—38

2.Кацюба  О.А.,  Жданов  А.И.  Особенности  применения  МНК  для  оценивания  линейных  разностных  операторов  в  задачах  идентификации  объектов  управления  //  Автоматика  и  телемеханика.  —  1979.  —  №  8.  —  с.  86—95.

3.Гантмахер  Ф.Р.  Теория  матриц.  М.:  Физматлит,  2010.