ЧИСЛЕННОЕ  МОДЕЛИРОВАНИЕ  ФРЭЭ  ВЫСОКОВОЛЬТНОГО  ИМПУЛЬСНОГО  РАЗРЯДА  ПУЧКОВОГО  ТИПА  МЕТОДОМ  МОНТЕ-КАРЛО  С  САМОСОГЛАСОВАНИЕМ

Борисов  Алексей  Владимирович

канд.  физ.-мат.  наук,  доцент  национального  исследовательский  Томского  государственного  университета  г.  Томск

E-mail:  borisov@phys.tsu.ru

Демкин  Владимир  Петрович

д-р  физ.-мат.  наук,  зав.  кафедрой  общей  и  экспериментальной  физики,  профессор  национального  исследовательский  Томского  государственного  университета  г.  Томск

Мельничук  Сергей  Васильевич

канд.  физ.-мат.  наук,  доцент  национального  исследовательский  Томского  государственного  университета  г.  Томск

Заседатель  Вячеслав  Сергеевич

старший  преподаватель  национального  исследовательский  Томского  государственного  университета  г.  Томск

NUMERICAL  SIMULATION  OF  EEDF  OF  HIGH-VOLTAGE  IMPULSING  ATOMIC  BEAM  DISCHARGE  BY  MONTE  CARLO  METHOD  WITH  SELF-CONSISTENCY

Aleksey  Borisov

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  National  Research  Tomsk  State  University,  Tomsk

Vladimir  Demkin

doctor  of  Physical  and  Mathematical  Sciences,  Head  of  the  Chair  of  General  and  Experimental  Physics,  professor  of  National  Research  Tomsk  State  University,  Tomsk

Sergey  Melnichuk

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  National  Research  Tomsk  State  University,  Tomsk

Vyacheslav  Zasedatel

head  teacher  of  National  Research  Tomsk  State  University,  Tomsk

АННОТАЦИЯ

В  данной  работе  проведено  численное  моделирование  функции  распределения  электронов  по  энергиям  (ФРЭЭ)  высоковольтного  импульсного  разряда  пучкового  типа  методом  Монте-Карло.  Найдены  функции  распределения  электронов  в  межэлектродном  зазоре  с  электрическим  полем  и  в  факеле  плазмы  в  приближении  нулевого  электрического  поля.  Расчет  ФРЭЭ  в  факеле  плазмы  проведен  с  использованием  процедуры  самосогласования.  Данная  процедура  позволяет  корректно  рассчитать  ФРЭЭ  во  всем  диапазоне  энергий. 

АННОТАЦИЯ

In  this  research  there  is  conducted  a  numerical  simulation  of  electron  energy  distribution  function  (EEDF)  of  high-voltage  impulsing  atomic  beam  discharge  by  Monte  Carlo  method.  There  are  found  electron  distribution  functions  in  interelectrode  gap  with  an  electric  field  and  in  plasma  flame  in  a  zero  electric  field.  EEDF  computation  in  plasma  flame  is  performed  with  a  use  of  self-consistency.  This  procedure  allows  correctly  computing  EEDF  in  full  range  of  energies. 

Ключевые  слова:  ФРЭЭ;  метод  Монте-Карло;    плазма;  самосогласование.

Keywords:  EEDF;  Monte  Carlo  method;    plasma;  self-consistency.

В  данной  работе  проведено  численное  моделирование  ФРЭЭ  высоковольтного  импульсного  разряда  пучкового  типа  методом  Монте-Карло,  описанным  в  работах  [4—5].  Вычислительная  модель  построена  для  описания  поведения  электронов  в  межэлектродном  зазоре  длиной  1  мм  и  в  факеле  плазмы  в  приближении  нулевого  электрического  поля  с  параметрами  разряда,  взятыми  из  работы  [6].  Геометрия  разряда  представлена  на  рис.  1.  В  качестве  примера,  вид  электрического  поля  соответствующий  максимуму  тока  разряда  в  зависимости  о  расстояния  до  катода  показан  на  рис.  2.  Разряд  считается  квазистационарным.  Численное  моделирование  проводилось  для    смеси  газов  с  давлениями  9  и  0,5  Торр  соответственно.

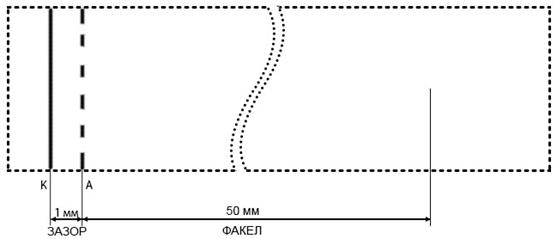
Рисунок  1.  Схема  газоразрядного  источника

Рисунок  2.  Зависимость  напряженности  электрического  поля  от  расстояния  до  катода

В  межэлектродном  зазоре  с  большим  по  величине  значением  ускоряющего  электрического  поля  существенное  влияние  на  ФРЭЭ  оказывают  реакции  ионизации,  возбуждения  и  упругого  удара.  Численное  моделирование  проводится  с  использованием  обычной  схемы,  описанной  в  работе  [5].  Реакции  ионизации,  возбуждения  и  упругого  удара  для    использовались  такие  же,  как  в  [4],  а  их  сечения  взяты  из  работы  [4].  Для    учитывались  следующие  реакции:

Таблица  1.

Реакции,  выделенные  в  таблице  1  в  отдельные  блоки,  включены  в  схему  расчета  одинаковым  образом.

На  рис.  3  показана  функция  распределения  электронов  по  энергиям  в  межэлектродном  зазоре  для    плазмы  в  зависимости  от  расстояния  до  катода  для  момента  времени  соответствующего  электрическому  полю  представленному  на  рис.  2.

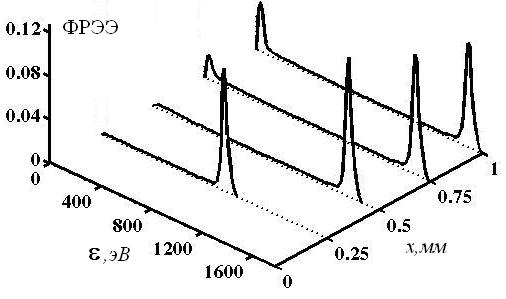
Рисунок  3.  Функция  распределения  электронов  по  энергиям  в  межэлектродном  зазоре    плазмы

Из  рис.  3  видно,  что  в  межэлектродном  зазоре  функция  распределения  электронов  имеет  два  выделенных  пика,  соответствующих  быстрым  и  медленным  электронам,  между  которыми  она  принимает  практически  постоянное  значение.  Расположение  второго  пика  по  оси  энергий  и  его  полуширина  характеризуют  пучок  «убегающих»  электронов  пролетающий  сквозь  анод  в  факел  плазмы.

В  факеле  плазмы  в  приближении  нулевого  электрического  поля  данная  схема  недостаточна,  так  как  помимо  реакций  ионизации,  возбуждения  и  упругого  удара  необходимо  учитывать  реакции  электрон-ионной  рекомбинации,  электрон-электронных  и  электрон-ионных  столкновений,  учет  которых  зависит  от  концентрации  ,  ,  а  также  от  искомой  функции  распределения  электронов.  Это  обусловлено  тем,  что  в  факеле  количество  медленных  электронов  достаточно  большое,  и  они  захватываются  ионами.  При  расчете  факела  плазмы  дополнительно  учтен  вклад  следующих  реакций:

Таблица  2.

Отметим,  что  в  межэлектродном  зазоре  эти  реакции  нами  не  учитывались  из  за  большой  средней  энергии  электронов  и  соответственно  малых  значений  сечений  этих  реакций.

Численное  моделирование  разряда  пучкового  типа  методом  Монте-Карло  в  факеле  плазмы  в  приближении  нулевого  электрического  поля  проведено  с  использованием  процедуры  самосогласования.  Эта  процедура  основана  на  предположении,  что  процессы  ионизации,  возбуждения,  упругого  удара,  диссоциации,  рекомбинации,  электрон-электронных  и  электрон-ионных  столкновений  находятся  в  динамическом  равновесии  в  квазистационарном  случае,  а,  следовательно,  можно  модифицировать  метод  Монте-Карло,  описанный  в  [5],  следующим  образом: 

1.  Функция  распределения  электронов  считается  найденной,  т.  е.  задается  первое  приближение  для  ФРЭЭ.

2.  Каждый  последующий  электрон,  проходя  через  фазовое  пространство,  вносит  малое  возмущение  в  функцию  распределения,  и  изменяет  ее.  Изменение  функции  распределения  происходит  только  после  того,  как  закончен  расчет  электрона  вылетевшего  из  межэлектродного  зазора  и  всех  вторичных  электронов  рожденных  им.

3.  Измененная  функция  распределения  используется  в  качестве  исходной  для  следующего  электрона,  вылетевшего  из  межэлектродного  зазора.

Данная  процедура  повторяется,  пока  изменение  функции  распределения  не  станет  пренебрежимо  малым.

Распределение  электронов  по  энергиям  на  аноде  при  расчете  ФРЭЭ  в  факеле  плазмы  было  взято  из  результатов  численного  моделирования  ее  в  ускоряющем  зазоре  (рис.  3)  при  x=1  мм.

На  рис.  4  показана  рассчитанная  функция  распределения  электронов  по  энергиям  в  факеле    плазмы  в  зависимости  от  расстояния  до  анода.

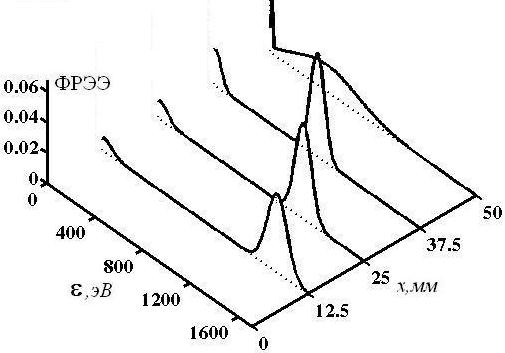
Рисунок  4.  Функция  распределения  электронов  по  энергиям  в  факеле    плазмы

Из  рис.  4  видно,  что  в  факеле    плазмы  функция  распределения  электронов  изменяется  с  расстоянием  до  анода  таким  образом,  что  пик  соответствующий  быстрым  электронам  сдвигается  в  сторону  меньших  энергий  и  его  полуширина  становится  больше.  В  результате  реакций  ионизации,  возбуждения,  упругого  удара,  диссоциации,  электрон-электронных  и  электрон-ионных  столкновений  происходит  перенос  электронов  из  области  высоких  энергий  в  область  низких.

Таким  образом,  для  медленных  электронов  расчет  ФРЭЭ  по  методу  Монте-Карло,  описанному  в  работе  [5],  приводит  к  огромным  вычислительным  сложностям.  Разработанная  нами  процедура  самосогласования  дает  возможность  корректно  рассчитать  ФРЭЭ  во  всем  диапазоне  энергий. 

Список  литературы:

1.Алхазов  Г.Д.  //  ЖТФ.  —  1970.  —  Т.  50.  —  Вып.  1.  —  С.  97—107.

2.Бабичев  А.П.,  Бабушкина  Н.А.,  Баратковский  А.М.  и  др.  Физические  величины:  Справочник.  М.:  Энергоатомиздат.  —  1991.  —  1232  с.

3.Голант  В.У,  Жлинский  А.П.,  Сахаров  И.Е.  Основы  физики  плазмы.  Атомиздат,  1977.  —  384  с. 

4.Демкин  В.П.,  Королев  Б.В.,  Мельничук  С.В.//  Физика  плазмы.  —  1995.  —  Т.  21.  —  №  1.  —  С.  81—84.

5.Boeuf  J.P.,  Marode  E.A  Monte  Carlo  analysis  of  an  electron  swarm  in  a  nonuniform  field:  the  cathode  region  of  a  glow  discharge  in  helium  //  J.  Phys.  D:  Appl.  Phys.,  15  (1982)  2169—2187.  Printed  in  Great  Britain.

6.Demkin  V.P.,  S.V.  Melnichuk,  A.V.  Borisov,  B.S.  Semukhin,  S.S.  Bardin,  Russian  Physics  Journal.  55,  1222  (2013).

7.Tabata  T.  et  al./  Atomic  Data  and  Nuclear  Data  Tables.  —  2006.  —  Vol.  92.  —  P.  375—406.

8.Yu  Z.,  J.J.  Rocca  and  G.J.  Collins,  J.  Appl.  Phys.  54(1),  131  (1983).