Статья опубликована в рамках: XII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 11 ноября 2013 г.)
Наука: Физика
Секция: Физика магнитных явлений
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ЗАВИСИМОСТЬ МАКСИМУМА ТАНГЕНЦИАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ РАССЕЯНИЯ ОТ РАССТОЯНИЯ ДО ЦЕНТРА НЕКРУГОВЫХ СИММЕТРИЧНЫХ ЦИЛИНДРИЧЕСКИХ ДЕФЕКТОВ
Черепанов Артём Алексеевич
аспирант кафедры прикладной физики, ПНИПУ, г. Пермь
Email: archerepanov@gmail.com
Кротов Лев Николаевич
д-р физ.-мат. наук, доцент, зав. кафедрой прикладной физики ПНИПУ, г. Пермь
Email:
DEPENDENCY OF TANGENTIAL CONSTITUENT'S MAXIMUM OF MAGNETIC FIELD DISPERSION FROM THE DISTANCE TO THE CENTRE OF NON-CIRCULAR SYMMETRIC CYLINDRICAL DEFECTS
Artem Cherepanov
postgraduate student of the Department of Applied Physics, Perm National Research Polytechnic University, Perm
Lev Krotov
doctor of Physics and Mathematics, Head of the Department of Applied Physics, associate professor of Perm National Research Polytechnic University, Perm
АННОТАЦИЯ
В статье раскрываются проблемы определения глубины внутренних дефектов различных форм на основе аналитического решения прямой задачи магнитостатики. Методом вычислительного эксперимента исследована зависимость максимума тангенциальной составляющей магнитного поля рассеяния от расстояния до центра некруговых симметричных цилиндрических дефектов. Проведен анализ влияния размеров и геометрии дефектов на данную зависимость.
ABSTRACT
The article reveals the problems of detection of depth of inner defects of various shapes on the basis of analytical solution of primary problem of magnetostatics. Dependency of tangential constituent's maximum of magnetic field dispersion from the distance to the centre of non-circular symmetric cylindrical defects has been studied by applying the method of calculating experiment. The analysis of an influence of sizes and geometry of the defects on the given dependency has been undertaken.
Ключевые слова: магнитостатика; дефект; ферромагнетик; вычислительный эксперимент.
Keywords: magnetostatics; defect; ferromagnetic; calculating experiment.
Постановка прямой задачи магнитостатики для кругового цилиндрического дефекта на бесконечной ферромагнитной плоскости, геометрически представленная на рисунке 1, рассматривалась многими авторами. Применительно к проблеме магнитных методов неразрушающего контроля эта постановка прямой задачи магнитостатики и аналитическое решение её в приближении линейности магнитных свойств ферромагнетика приведены в работе Щербинина В.Е. и Горкунова Э.С. [1].
Для тангенциальной и нормальной составляющих магнитного поля кругового цилиндрического дефекта в [1] получены соотношения
![]() (1)
(1)
![]() (2)
(2)
Здесь H0 — намагничивающее поле, R — радиус дефекта, µ1, µ2 — магнитные проницаемости ферромагнетика и среды внутри дефекта, x, y — координаты точки, в которой рассчитываются величины Hx, Hy.
Из (1) и (2) следует, что поле цилиндрического дефекта в среде µ=const и однородном намагничвающем поле H0 по своей структуре совпадает с полем дипольной нити, расположенной в центре дефекта и имеющей дипольный момент
![]() (3)
(3)
Тангенциальная составляющая Hx при X=0 имеет максимум, для которого справедливо соотношение
![]() (4)
(4)
Здесь YС — расстояние от центра дефекта до точки регистрации магнитного поля.
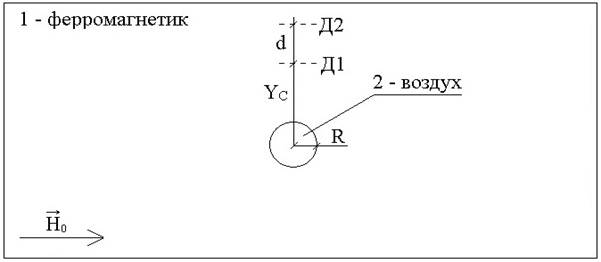
Рисунок 1. Геометрия задачи магнитостатики с круговым дефектом
Введем в рассмотрение тангенциальную составляющую магнитного поля рассеяния от дефекта, нормированную на величину намагничивающего поля – hxmax. В точках X=0, YC и X=0, YC + d для максимумов тангенциальной составляющей в соответствии с (4) получим
![]() (5)
(5)
![]() (6)
(6)
Из отношения полей следует
![]() (7)
(7)
или
![]() (8)
(8)
Координата центра дефекта — YC из соотношения (8) может быть найдена по формуле
![]() (9)
(9)
По формуле (9) можно по двум измерениям магнитного поля рассеяния определить искомое расстояние от ближнего датчика магнитного поля до центра кругового цилиндрического дефекта в безграничной (или очень большой) ферромагнитной области.
Формула (9) также применима для определения расстояния до центра некруговых симметричных цилиндрических дефектов, однако точность получаемых при этом результатов во многом зависит от того, как соотношение (5) выполняется для таких дефектов.
Для исследования зависимости hxmax(YС) для некруговых симметричных цилиндрических дефектов проведён вычислительный эксперимент, реализованный на базе пакета прикладных программ МАТЛАБ версии 7.12.0.635.
Рассмотрены дефекты в форме эллипса и прямоугольника, геометрия задач представлена на рисунке 2 и рисунке 3, соответственно.
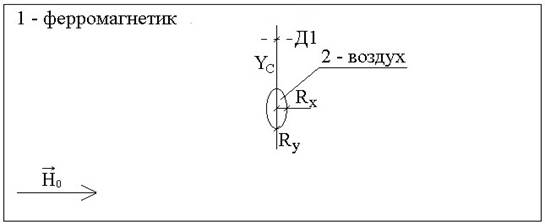
Рисунок 2. Геометрия задачи магнитостатики с дефектом в форме эллипса
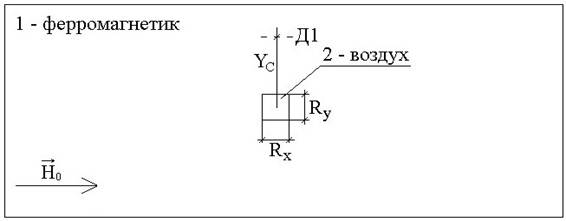
Рисунок 3. Геометрия задачи магнитостатики с дефектом в форме прямоугольника
Для дефектов различных размеров произведён расчёт максимума тангенциальной составляющей магнитного поля рассеяния hxmax на различных расстояниях YС до центра дефекта. Полученные результаты приведены в таблице 1 и таблице 2 для дефектов в форме эллипса и прямоугольника, соответственно. Графически полученные результаты представлены на рисунке 4 и рисунке 5, соответственно.
Таблица 1.
Результаты вычислительного эксперимента для дефекта в форме эллипса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.
Результаты вычислительного эксперимента для дефекта в форме прямоугольника
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализируя полученные результаты, можно сделать вывод, что соотношение (5), полученное для кругового цилиндрического дефекта, не выполняется для дефектов в форме эллипса и прямоугольника, что может являться причиной возникновения погрешностей при использовании математической модели (9) для определении расстояния до центра таких дефектов.
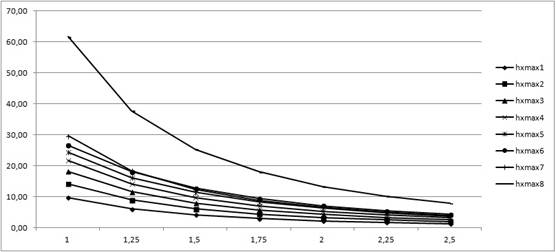
Рисунок 4. Результаты вычислительного эксперимента для дефекта в форме эллипса
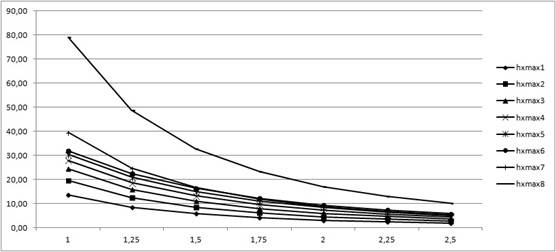
Рисунок 5. Результаты вычислительного эксперимента для дефекта в форме прямоугольника
Для повышения точности математической модели необходимо найти подходы к решению обратной задачи магнитостатики, учитывающие форму и размеры дефекта.
Список литературы:
1.Щербинин В.Е. Горкунов Э.С. Магнитный контроль качества металлов. Екатеринбург: УрО РАН, 1996.
дипломов


Оставить комментарий