Статья опубликована в рамках: XII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 11 ноября 2013 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТРИЦЫ ТОРСИОННЫХ ПРЕОБРАЗОВАНИЙ
Мисюра Наталья Евгеньевна
старший преподаватель ИНФО УРФУ, г. Екатеринбург
E-mail: n_misura@mail.ru
Жилин Сергей Сергеевич
магистрант ВШЭМ УРФУ, г. Екатеринбург
E-mail: gss.1@mail.ru
MATRICES OF TORSIONAL TRANSFORMATIONS
Natalia Musyura
head teacher of Institute of Fundamental Education of Ural Federal University, Ekaterinburg
Sergey Zhilin
master’s degree student of Graduate School of Economics and Management of Ural Federal University, Ekaterinburg
АННОТАЦИЯ
Цель работы проиллюстрировать математический метод торсионного преобразования объёмных форм. Математический метод основывается, на нелинейном преобразовании трехмерного евклидова пространства. Представленный метод является наглядным, практически значимым для современного формообразования в архитектуре.
ABSTRACT
The aim of this article is to illustrate a mathematical method of torsional transformation of three-dimensional configurations. The mathematical method is based on a nonlinear transformation of tridimensional Euclidian space. This method appears to be a descriptive and relevant for practical purposes for modern shaping in architecture.
Ключевые слова: торсионное формообразование, математическое моделирование в архитектуре, матрица торсионного преобразования
Keywords: torsional shaping; mathematical modeling in architecture; matrix of torsional transformation.
Одним из современных специфических средств создания особой архитектурной выразительности при строительстве высотных зданий является придания им спиралевидной формы. При этом создается визуальный динамический эффект, ассоциирующийся в сознании наблюдателя с такими уникальными природными явлениями, как торнадо и тайфуны. Основоположниками этого направления в архитектуре являются выдающиеся архитекторы А.В. Коротич и С. Калатрава.
А.В. Коротич является автором «Теории модифицированных регулярных сетей», которая служит научной платформой для создания современных прогрессивных методик кристаллографического, торсионного и фрактального формообразования в архитектуре, а также автором 16 новых способов моделирования составных линейчатых оболочек, используемых при решении композиционных задач архитектурного формообразования. Методы торсионного формообразования нашли отражение в проектных работах 2005 года, представленных на рис. 1 [1—2].

Рисунок 1. Торсионное формообразование А.В. Коротича
Торсионное формообразование было использовано в 2007 году С. Калатравой при проектировании высотного здания «Чикагский шпиль» (рис. 2).

Рисунок 2. Чикагский шпиль С. Калатравы [4]
В основу торсионного формообразования может быть положен математический метод нелинейного преобразования трехмерного евклидова пространства, представленный матричным равенством:
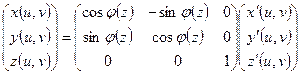 . (1)
. (1)
Здесь  — вектор-столбец, задающий структурный элемент здания до его закручивания,
— вектор-столбец, задающий структурный элемент здания до его закручивания, 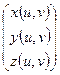 — вектор-столбец, задающий структурный элемент здания в окончательной композиции,
— вектор-столбец, задающий структурный элемент здания в окончательной композиции, ![]() — непрерывная функция, определяющая угол поворота произвольного горизонтального сечения здания.
— непрерывная функция, определяющая угол поворота произвольного горизонтального сечения здания.
В качестве иллюстрации применения матрицы торсионного преобразования рассмотрим формообразование четырехгранного высотного здания, боковые поверхности которого получаются закручиванием линейчатых поверхностей, имеющих первоначально форму эллиптических цилиндров (рис. 3).

Рисунок 3. Модель четырёхгранного здания до торсионного преобразования
Исходным структурным элементом здания является клиновидная поверхность, которая задается уравнением эллиптического цилиндра
|
|
|
ограниченного плоскостями
![]() ,
, ![]() ,
,
где: ![]() — радиус окружности, описанной около основания здания,
— радиус окружности, описанной около основания здания,
![]() и
и ![]() — полуоси эллипса,
— полуоси эллипса,
![]() — половина внутреннего угла сектора здания (см. рис. 4),
— половина внутреннего угла сектора здания (см. рис. 4),
![]() — количество сторон основания здания.
— количество сторон основания здания.
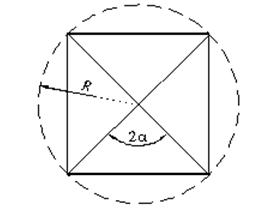
Рисунок 4. Схема основания здания
Полуоси эллипса (см. рис. 5) можно выразить через конструктивные параметры здания, подставляя в уравнение (2) координаты точки A и вводя обозначение ![]() :
:
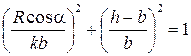 .
.
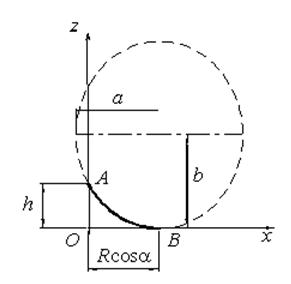
Рисунок 5. Сечение эллиптического цилиндра
Отсюда
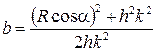 и
и 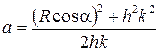 .
.
Математическая модель клина в форме элемента линейчатой цилиндрической поверхности описывается уравнением
![]() ,
, ![]() ,
, ![]() ,
,
где 
и  — функции, задающие направляющие кривые элемента линейчатой поверхности.
— функции, задающие направляющие кривые элемента линейчатой поверхности.
Элементы остальных клиньев здания получены поворотом первого клина относительно оси Oz на углы ![]() ,
, ![]() и
и ![]() с помощью соответствующих матриц аффинного преобразования:
с помощью соответствующих матриц аффинного преобразования:
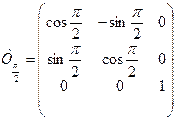 ,
,  ,
, 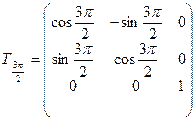 .
.
Боковые поверхности здания до его торсионного закручивания определяются следующими матричными уравнениями:
![]() .
.
Вводя в уравнение (1) матрицу торсионного преобразования, обеспечивающую постоянный угол закручивания на каждую единицу высоты здания
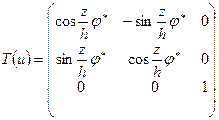 ,
,
где: — ![]() — полный угол закручивания;
— полный угол закручивания;
уравнения структурных элементов здания можно записать в следующем виде:
![]() .
.
Модель здания после торсионного закручивания представлена на рис.6. При необходимости закручивания в противоположном направлении матрица торсионного преобразования транспонируется.
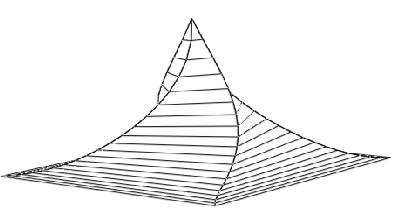
Рисунок 6. Модель четырехгранного здания после торсионного преобразования
Предложенный алгоритм формообразования структурных элементов высотных зданий позволяет путем применения матриц торсионных преобразований достаточно быстро выполнить геометрическое моделирование в одном из пакетов символьной математики с встроенным графическим редактором, предваряющее дизайнерскую и архитектурную проработку. Кроме того, это позволяет в дальнейшем удешевить проектные работ![]() за счет возможностей получения цифровых массивов, определяющих конструктивные параметры элементов здания.
за счет возможностей получения цифровых массивов, определяющих конструктивные параметры элементов здания.
Применение матрицы торсионного преобразования нашло отражение в призовом проекте реконструкции телевизионной башни г. Екатеринбурга (рис. 7) .

Рисунок 7. Призовой проект реконструкции телебашни г. Екатеринбурга
Список литературы:
1.История тентовой архитектуры// [Электронный ресурс] — Режим доступа. — URL режим доступа http://www.tentmax.ru/information/history/ (дата обращения15.09.2013).
2.Коротич М.А. Композиционное развитие высотной архитектуры// Академический вестник УРАЛНИИПРОЕКТ РААСН — 2010 — № 4, — с. 96—101.
3.Коротич М.И. Торсионное и фрактальное формообразование в архитектуре [Электронный ресурс] — Режим доступа. — URL: http://www.raasn.ru/persons/o_arch/korotich.htm(дата обращения 20.10.2013).
4.Santiago Calatrava [Электронный ресурс] — Режим доступа — URL: http://www.chicagoarchitecture.info/Building/357/The-Chicago-Spire.php&usg ( дата обращения 01.11.2013).
дипломов


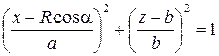 ,
,
Оставить комментарий