РАСЧЕТ  МИГРАЦИИ  ЗАРЯДА  ПО  ЦЕПИ  ДНК  С  УЛУЧШЕННЫМИ  ПАРАМЕТРАМИ

Бойда  Денис  Леонидович

магистрант,  Дальневосточный  федеральный  университет,  Владивосток

E-mail: 

Подоба  Диана  Александровна

студентка,  Дальневосточный  федеральный  университет,  Владивосток

E-mail: 

Ширмовский  Сергей  Эдуардович

канд.  физ.-мат.  наук,  доцент,  Дальневосточный  федеральный  университет,  Владивосток

E-mail: 

CALCULATION  OF  CHARGE  MIGRATION  THROUGH  DNA  SEQUENCE  WITH  IMPROVED  PARAMETRS

Boyda  Denis  Leonidovich

master  student,  Far  Eastern  Federal  University,  Vladivostok

Podoba  Diana  Aleksandrovna

student,  Far  Eastern  Federal  University,  Vladivostok

Shirmovsky  Sergey  Ehduardovich

ph.D.,  Associate  Professor,  Far  Eastern  Federal  University,  Vladivostok

АННОТАЦИЯ

В  настоящей  работе  произведен  расчет  миграции  положительного  заряда  по  трем  различным  последовательностям  оснований  ДНК:  GATGGG,  ATCGACAAA,  AGGCGAGTG.  Для  расчета  использовалась  нелинейная  квантово-классической  модель.  Результаты  получены  с  использование  точных  параметров  для  моделирования  водородной  связи.  Анализируется  миграция  заряда  по  цепи  ДНК  и  деформация  самой  молекулы  под  воздействием  этой  миграции.  Результаты  с  точными  параметрами  сравниваются  с  полученными  ранее  результатами  для  усредненных  параметров.

ABSTRACT

Positive  charge  migration  through  DNA  sequences:  GATGGG,  ATCGACAAA,  AGGCGAGTG  was  calculated.  The  process  was  investigated  on  the  basis  of  nonlinear  quantum-classical  model.  The  results  were  calculated  with  realistic  hydrogen  bond  parameters.  The  charge  migration  and  DNA  deformation  have  been  analyzed.  Results  with  realistic  parameters  are  compared  with  results  are  being  calculated  in  average  parameters  case.

Ключевые  слова:  ДНК;  миграция  заряда;  нелинейная  динамика;  квантовая  механика.

Keywords:  DNA;  charge  migration;  nonlinear  dynamic;  quantum  mechanics.

Данная  работа  выполнена  при  поддержке  Фонда  Дмитрия  Зимина  «Династия»

В  настоящее  время  широко  исследуется  миграция  заряда  по  цепи  ДНК.  Это  связанно  с  тем,  что  миграция  заряда  может  приводить  к  повреждению  молекулы  ДНК,  которое  лежит  в  основе  многих  радиационно-индуцированных  эффектов,  связанных  с  гибелью  клеток,  индукции  хромосомных  аберраций,  генетических  мутаций  и  злокачественных  трансформаций. 

Исследовать  миграцию  заряда  по  цепи  ДНК  и  при  этом  учитывать  деформацию  самой  молекулы  возможно  в  квантово-классической  модели  [4],  [2].  Обсудим  ее  подробней.

В  квантово-классической  модели  полная  энергия  системы:  ДНК-заряд  задается  следующим  образом:

Первое  слагаемое  описывает  молекулу  ДНК  с  помощью  формализма  классической  механики,  а  второе  —  средняя  энергия  заряда,  свойства  которого  задаются  квантовым  оператором  Гамильтона  .  Такое  разбиение  возможно  в  предположении,  что  молекула  ДНК  является  макроскопическим  объектом  по  сравнению  с  зарядом  —  микроскопическим  объектом. 

В  данной  модели  молекула  ДНК  представляется  как  система  пар  оснований,  расположенных  друг  над  другом  и  взаимодействующих  между  собой  посредством  сткэкинговой  связи.  Два  основания  объединяются  в  пару  и  удерживаются  водородной  связью.  Такая  система  в  работе  определяется  гамильтонианом  :

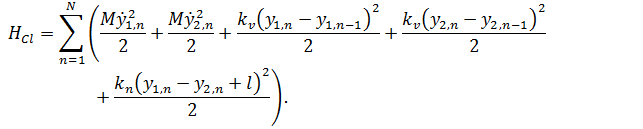
В  этом  выражении  первое  и  второе  слагаемое  описывают  кинетическую  энергию  оснований,  расположенных  на  первой  и  второй  цепочке  ДНК.  Поскольку  массы  оснований  равны  по  порядку  величины,  здесь  используется  средняя  масса  оснований  -  .  Второе  и  третье  слагаемые  задают  энергию  стэкингового  взаимодействия,  которое  в  нашей  модели  не  зависит  от  типа  оснований.  Строго  говоря,  стэкинговое  взаимодействие  для  разных  пар  оснований  может  характеризоваться  разными  значениями,  однако,  на  сегодняшний  день  нам  не  известны  точные  параметры  для  этого  типа  связей,  поэтому  в  нашей  модели  оно  одинаково  для  всех  пар  оснований,  где    —  силовая  константа  стэкиноговогй  связи.  Последнее,  пятое  слагаемое  определяет  энергию  водородных  связей.  Согласно  правилу  Чаргафа,  в  ДНК  возможны  только  два  типа  пар  оснований:  гуанин  —  цитозин  (в  дальнейшем  будем  их  обозначать  кратко:  G-C)  и  аденин-тимин  (A-T).  Причем  в  первой  паре  основания  удерживаются  тремя  водородными  связями,  а  во  второй  —  двумя.  В  этой  связи  силовая  константа  взаимодействия  будет  различна  для  различных  пар:    и    ,  данные  значения  взяты  из  работы  [3].  Суммирование  производится  по  всем  парам  оснований  рассматриваемой  цепи  длины  N.

Свойства  заряда  задаются  следующим  оператором  Гамильтона 

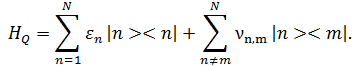
Здесь  первое  слагаемое  описывает  энергию  заряда  на  основании  n,  а  второе  энергию  перехода  заряда  с  n  на  m  основание.  Энергия  заряда  на  основании  задается  двумя  слагаемыми:  _.  Первое  слагаемое  является  статическим  и  задается  энергией  ионизации  основания  _,  а  второе  —  динамическое  и  зависит  от  величины  ,  которая  представляет  собой  растяжение  пары  оснований.  В  положении  равновесия  эта  величина  равна  нулю,  при  растяжении  меньше  нуля,  а  при  сжатии  больше  нуля.  Это  слагаемое  учитывает  все  неопределенные  явно  эффекты,  влияющие  на  энергию  ионизации:  деформацию  ДНК,  свойства  среды,  контр  ионные  движения  в  растворе  т.  д.  Параметр    является  подгоночным.  Все  значения  параметров  нами  взяты  из  работы  [4].

                             а)                                                             б)

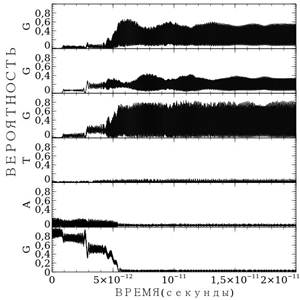
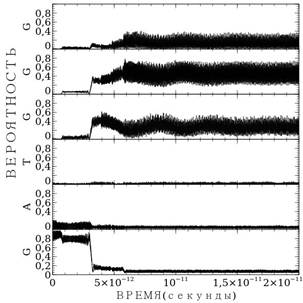
Рисунок  1.  Расчет  миграции  заряда  по  последовательности  GATGGG:  а)  —  для  случая  средних  параметров  водородной  связи;  б)  —  для  случая  точных  параметров

На  основе  канонических  уравнений  Гамильтона  с  учетом  сил  трения  и  уравнения  Шредингера  была  получена  система  из  3N  дифференциальных  уравнений,  которые  решались  численно  методом  Рунге-Кутта  4  порядка.

Рассмотрим  результаты  расчетов  миграции  заряда  по  последовательности  GATGGG  —  рис.  1.  Расчеты  выполнены  при  значении  подгоночного  параметра  .  На  рисунке  представлены  зависимости  вероятности  пребывания  заряда  на  основаниях  от  времени,  вероятности  пребывания  заряда  на  основаниях  расположены  друг  над  другом:  самый  нижний  —  вероятность  пребывания  на  первом  гуанине  G,  второй  —  на  аденине  А  и  т.  д.  Графики  имеют  вид  черных  широких  полос,  это  связано  с  тем,  что  вероятность  –  сильно  осциллирующая  величина,  и  в  данном  масштабе  осцилляции  сливаются.  На  рис.  1а  представлен  расчет  миграция  заряда  в  случае  средней  силовой  константы  водородной  связи    .  В  этом  случае  в  начальный  момент  времени  заряд  пребывал  на  первом  гуанине,  затем  постепенно  вероятность  пребывания  заряда  уменьшается.  Спустя  примерно  5.1*10^-12  секунд  заряд  покидает  первый  гуанин  и  локализуется  на  последних  трех  гуанинах  минуя  аденин  и  тимин,  посредством  туннельного  эффекта.  Далее  заряд  осциллирует  между  тремя  гуанинами,  где  вероятность  его  пребывания  максимальна.

На  рис.1б  представлен  тот  же  самый  расчет,  но  в  случае  реальных  параметров  водородных  связей  для  различных  пар  оснований.  Более  детальный  выбор  параметров  повлиял  на  особенности  миграции  заряда.  Заряд  мигрирует  более  стремительно.  Сократилось  время  миграции  заряда,  теперь  оно  составляет  4.6*10^-12  секунд.  Кроме  того,  изменилось  распределение  заряда  между  тремя  последними  гуанинами.  Теперь  максимальная  вероятность  пребывания  заряда  на  третьем  гуанине,  в  отличие  от  прошлого  раза,  когда  максимум  был  определён  на  втором  гуанине.  В  целом  характер  миграции  заряда  не  изменился.

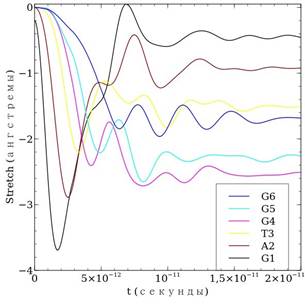
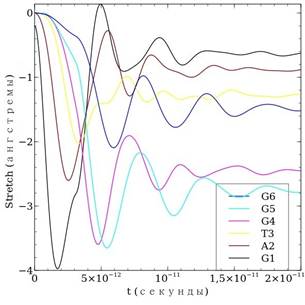
Теперь  рассмотрим  расчет  деформации  ДНК  для  той  же  последовательности  —  рис.  2.  Деформация  ДНК  анализируется  с  помощью  введенной  ранее  величины  stretch  =  _,  которая  представляет  собой  растяжение  пары  основания.  Заметим,  что  расстояние  между  центрами  оснований  одной  пары  в  положении  равновесия  нами  выбрано  равным  7  Å,  т.  е.  растяжение  равное  7  Å  соответствует  удлинению  на  100  %.  Кроме  того,  согласно  обзору  [1]  при  растяжение  пары  оснований  более  чем  на  1,5—2  Å  водородную  связь  можно  считать  разорванной.  Рассмотрим  расчеты.  В  начале  все  пары  оснований  рассчитанной  цепи  растягиваются  до  определенного  момента  времени  (примерно  в  этот  момент  времени  происходит  перескок  заряда),  когда  начинаются  колебания,  которые  в  последующем  затухают,  и  процесс  стабилизируется  —  растяжения  пар  основания  принимают  определенные  значения.  В  целом,  за  исключением  некоторых  деталей,  расчет  с  точными  параметрами  не  отличается  от  расчета  с  реальными  параметрами  водородной  связи. 

                            а)                                                         б)

Рисунок  2.  Расчет  деформации  последовательности  молекулы  ДНК  GATGGG  вследствие  миграции  заряда:  а)  —  для  случая  средних  параметров  водородной  связи;  б)  —  для  случая  точных  параметров

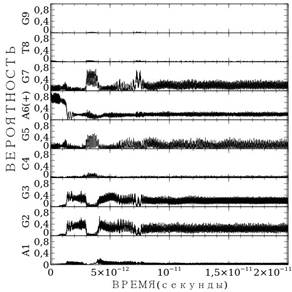
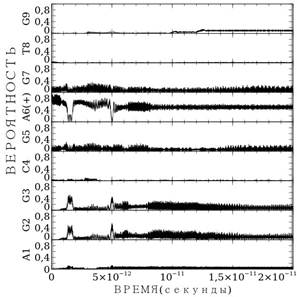
Теперь  рассмотрим  расчет  миграции  заряда  для  последовательности  AGGCGA(+)GTG  —  рис.  3.  На  данном  рисунке  знаком  (+)  помечен  аденин,  на  котором  находился  заряд  в  начальный  момент  времени.  Расчет  выполнен  при  значении  подгоночного  параметра  .  В  отличие  от  расчета  рис.  3а  более  точный  учет  параметров  водородной  связи  приводит  к  кардинальному  изменению  ситуации.  Если  в  случае  расчета  со  средними  параметрами  заряд  мигрирует  вдоль,  рассматриваемой  цепи  ДНК,  то  при  более  реалистичном  выборе  параметров,  при  данном  значении  параметра  миграция  заряда  отсутствует  —  заряд  остается  на  аденине  A6(+).

                             а)                                                       б)

Рисунок  3.  Расчет  миграции  заряда  по  последовательности  AGGCGA(+)GTG,:  а)  —  для  случая  средних  параметров  водородной  связи;  б)  —  для  случая  точных  параметров

Поскольку  процесс  миграции  во  многом  определяется  так  же  выбором  параметра  _,  в  работе  мы  нашли  значение  подгоночного  параметра,  при  котором  миграция  заряда  возможна.  На  рис.  4.  представлен  расчет  для  AGGCGA(+)GTG  последовательности  оснований.  В  этом  случае  значение  подгоночного  параметра  составляет  .  Теперь,  как  и  в  случае  цепи  GATGGG,  миграция  заряда  несущественно  отличается  от  случая  рис.  3а.  Однако,  поскольку  смысл  параметра  интенсивность  взаимодействия  заряда  с  парой  оснований,  то  мы  полагаем,  что  учет  реальных  параметр  водородной  связи  ведёт  к  уточнению  данной  величины.

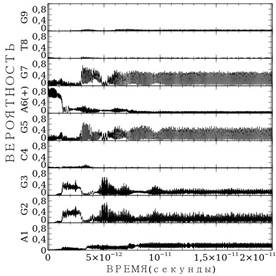
Рисунок  4.  Расчет  миграции  заряда  по  последовательности  AGGCGA(+)GTG  для  случая  реальных  параметров  водородной  связи

В  целом  более  точный  учет  значений  параметров  водородной  связи  незначительно  повлиял  на  динамику  миграции  заряда  по  последовательности  оснований  молекулы  ДНК  —  изменились  детали,  но  не  характер  миграции.  Кроме  того  он  позволил  несущественно  уточнить  значение  интенсивности  взаимодействия  заряда  с  парой  оснований.

Список  литературы:

1.Якушевич  Л.В.  Нелинейная  физика  ДНК:  НИЦ  «Регулярная  и  хаотическая  динамика»,  Институт  компьютерных  исследований  М.:  Ижевск,  2007,  —  252  с 

2.Fialko  N.S.,  Lakhno  V.D.  Nonlinear  dynamics  of  excitations  in  DNA//Physics  Letters  A  —  2000  —  №  278  —  p.  108—112.

3.Peyrard  M.  Nonlinear  dynamics  and  statistical  physics  of  DNA  //  Nonlinearity  —  2004  —  Vol.  17.  —  p.  r1—r40.

4.Shirmovsky  S.Eh.,  Boyda  D.L.  Study  of  DNA  conducting  properties:  Reversible  and  irreversible  evolution//Biophysical  Chemistry  —  2013  —  Vol.  180—181  October/November  —  p.  95—101