Статья опубликована в рамках: VI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 27 мая 2013 г.)
Наука: Информационные технологии
Секция: Автоматизация и управление технологическими процессами и производствами
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ДИАГНОСТИКА И ПОВЫШЕНИЕ ТОЧНОСТИ ОЦЕНКИ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ЗА СЧЕТ ИНФОРМАЦИОННОЙ ИЗБЫТОЧНОСТИ (НА ПРИМЕРЕ РЕАКТОРНОГО БЛОКА УСТАНОВКИ КАТАЛИТИЧЕСКОГО РИФОРМИНГА)
Гайдамак Алексей Витальевич
магистрант УГНТУ, г. Уфа
Веревкин Александр Павлович
д-р техн. наук, профессор, г. Уфа
E-mail: apverevkin@mail.ru
Каталитический риформинг (КР) — это процесс, технологический режим которого зависит от характеристик сырья и катализатора, водородосодержащего газа и др. параметров, не все из которых могут быть измерены или же измеряются в лабораторных условиях. Это приводит к необходимости использования в системах автоматизации управления установками опыта экспертов. На технологический процесс накладываются жесткие ограничения на значения температуры, концентраций и давлений в аппаратах реакторного блока (РБ), которые необходимы для получения заданных показателей качества (ПК) выпускаемой продукции.
Важным аспектом является не только контроль за состоянием самого процесса, но и диагностика исправности измерительного оборудования, достоверность данных, получаемых с него. Это приводит к необходимости использования систем диагностики исправности информационно-измерительных каналов как составляющих комплексной системы автоматизации.
При управлении сложным технологическим объектом практически нельзя обойтись без моделирования процессов работы установки. Поскольку формальные модели оценивают ПК на основе измерения технологических параметров, возможные погрешности измерений могут привести к неоднозначности, нефизичности оценки показателей. В связи с этим возникает необходимость диагностики исправности измерительных каналов и обеспечения условий сохранения адекватности моделей, например, на основе контроля диапазонов варьирования переменных [1, 2].
Целью настоящей работы является создание методов моделирования РБ установки КР, позволяющих:
·повысить точность оценки по моделям;
·диагностировать исправность датчиков и информационно- измерительных каналов.
Для достижения поставленной цели были сформулированы и решены следующие задачи:
·провести анализ предпочтительности базиса для моделирования реакторных процессов, разработать модели для решения задач повышенния точности и диагностического инструментария;
·разработать методику диагностики достоверности данных при моделировании;
·разработать метод диагностических процедур идентификации исправности датчиков и информационно-измерительных каналов системы управления (для измерения Т-реакторов).
·разработать метод моделирования РБ установки КР с повышением точности оценки по моделям на основе использования информационной избыточности.
За исходные данные для проведения работы были взяты значения температуры, давления в реакторах блока КР, расход подаваемого сырья, дихлорэтана, а так же температуры начала кипения, выкипания 10 %, 50 % и октановые числа продукта на интервале от 22.09.2011 по 09.07.2012.
Для моделирования реакторных процессов предпочтительнее использовать обратные модели — это обычно формальные модели типа «черный» или «серый» ящик. По сути своей такие модели являются диагностическими и вероятностными, поскольку получаются на основе статистической информации о входах-выходах объекта и эвристических знаний о закономерностях процессов в объекте. В силу того, что исходные данные, по большей части, имеют статистический характер, в данном исследовании моделирование РБ базирутся на уравнениях регрессии. Расчёт по ним проводится за существенно меньшее время, адаптация таких моделей под конкретный процесс дешевле и быстрее [1, 6].
На первоначальном этапе исследования был проведен анализ исходных данных, в ходе которого были выявлены закономерности для дальнейшего моделирования:
·характер изменения температур на входах реакторов (рисунок 1) практически не изменяется, что позволяет в расчетах заменить эти температуры одним усредненным значением — Твх;

Рисунок 1. Температуры на входах реакторов
·температуры на выходах реакторов различаются по величине, но по характеру поведения подобны друг другу (рисунок 2), поэтому в рассмотрение вводится и средняя температура по выходам — Твых;

Рисунок 2. Температуры на выходах реакторов: нижняя кривая — для Р2, средняя — Р3, верхняя — Р4
·так же давления на входах и выходах реакторов отличаются по величине, но близки по характеру поведения (рисунок 3), поэтому вводится среднее давление в реакторах — Рср.

Рисунок 3. Давления на входах и выходах реакторов
Один из методов диагностирования исправности измерительных каналов основан на использовании избыточного числа моделей для вычисления ПК, для реакторного блока установки риформинга — это значение октанового числа (ОЧ) бензина. Набор моделей в виде уравнений регрессии полиномиального типа для расчета ОЧ может быть получен для различных зон реакторов на множествах технологических параметров, часть из которых одинаковые, а часть различны.
Регрессионные модели имеют следующий вид:
·ОЧ1 = F (Твх.; FQ), FQ = {Fбенз.сГО4; Fгидроген.поток1; Fгидроген.поток2; Fкатализата; Fдхэ; Pср.; Tнк.катализата; Tнк.гидрогениз};
·ОЧ2 = F (Твых.; FQ);
·ОЧ3 = F (Тсекц.1-1; FQ);
·ОЧ4 = F (Тсекц.1-2; FQ);
·ОЧ5 = F (Тсекц.1-3; FQ);
·ОЧ6 = F (Тсекц.2-1; FQ);
·ОЧ7 = F (Тсекц.2-2; FQ);
·ОЧ8 = F (Тсекц.2-3; FQ);
·ОЧ9 = F (Твх.; Твых.; Тсекц.1-1; Тсекц.1-2; Тсекц.1-3; Тсекц.2-1; Тсекц.2-2; Тсекц.2-3; Fбенз.с ГО-4;Fкатализата;Fдхэ;Pср.).
Уравнение регресии в общем виде:
yi = bo + b1xi1 + ... + bk xik+ ei , i = 1...n, (1)
где: ei — некоррелированные случайные величины.
Коэффициенты регрессии b, стоящие перед входыми параметрами в моделях (Твх.; Твых.; Тсекц.1-1; Тсекц.1-2; Тсекц.1-3; Тсекц.2-1; Тсекц.2-2; Тсекц.2-3), должны быть достаточно велики. Это объясняется тем, что при изменении значений температур (более 400˚С) РБ, влияние малых коэффициентов на результат (ОЧ) будет незначительно и информационная значимость таких моделей будет соответственно мала.
Методика диагностики достоверности данных при моделировании реализуется при помощи статистики и регрессионного анализа, проводимого по полученным моделям.
Для соотношения (1) удобно использовать запись в матричной форме:
Y = Xb + e , (2)
Строится оценка коэффициентов регресии ![]() для вектора b так, чтобы вектор оценок
для вектора b так, чтобы вектор оценок ![]() = Х
= Х![]() зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора Y заданных значений.
зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора Y заданных значений.
Решением является (если ранг матрицы Х равен k +1) оценка:
![]() = (XTX)-1 XTY, (3)
= (XTX)-1 XTY, (3)
которая используется при моделировании вместо коэффициентов корреляции b.
Далее получаем коэффициент детерминации:
R2 =  . (4)
. (4)
Коэффициент R2 показывает качество подгонки регрессионной модели к наблюдаемым значениям yi. Если R2 = 0, то регрессия Y на x1 , ..., xk не улучшает качество предсказания. Другой крайний случай R2 = 1 означает точную подгонку: все ei = 0, т.е. все точки наблюдений лежат на регрессионной плоскости.
Проводится проверка гипотезы о нулевых значениях коэффициентов регрессии. Для проверки гипотезы Н0 об отсутствии какой бы то ни было линейной связи между y и совокупностью факторов, Н0: b1 = b2 = ... = bk = 0, т. е. об одновременном равенстве нулю всех коэффициентов, кроме коэффициента b0 при константе, используется статистика,
F =  =
=  =
=  , (5)
, (5)
если Н0 верна, по закону Фишера с k и n – k – 1 степенями свободы. Н0 отклоняется, если:
F > Fa (k, n – k – 1), (6)
где: Fa — квантиль уровня 1 — a.
Чему должено соответствовать малое значение уровеня значимости p<10-6.
В совокупности, по результатам изложенного выше анализа, исследуемые модели могут получить право быть диагностирующими, и в свою очередь использоваться как диагностический инструмент исправности средств измерений [2, 3].
Метод диагностических процедур идентификации исправности датчиков и информационно-измерительных каналов системы управления (для измерения Т реакторов) реализован на основе корреляционного анализа и полученных в ходе его коэффициентов корреляции. При этом должна быть обеспечена достоверность данных при моделировании.
Корреляционный анализ состоит в определении степени связи между двумя величинами X и Y. Коэффициент корреляции - характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:
 . (7)
. (7)
Коэффициент корреляции изменяется от –1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет [4].
Значения входной и выходной температур в одних моделях и температуры на срезах реакторов в других моделях имеют очень близкие значения коэффициентов корреляции с ОЧ и сильно коррелируют друг с другом (таблица 1).
Таблица 1.
Коэффициенты корреляции температур реакторов
|
|
Твх. |
Твых. |
Т1-1 |
Т1-2 |
Т1-3 |
Т2-1 |
Т2-2 |
Т2-3 |
|
Твх. |
1,0000 |
-0,1223 |
0,9924 |
0,1810 |
0,0311 |
0,9859 |
0,2617 |
-0,1208 |
|
Твых. |
-0,1223 |
1,0000 |
-0,1043 |
0,9302 |
0,9754 |
0,0108 |
0,8969 |
0,9950 |
|
Т1-1 |
0,9924 |
-0,1043 |
1,0000 |
0,1907 |
0,0444 |
0,9897 |
0,2683 |
-0,1041 |
|
Т1-2 |
0,1810 |
0,9302 |
0,1907 |
1,0000 |
0,9861 |
0,3153 |
0,9952 |
0,9359 |
|
Т1-3 |
0,0311 |
0,9754 |
0,0444 |
0,9861 |
1,0000 |
0,1687 |
0,9673 |
0,9801 |
|
Т2-1 |
0,9859 |
0,0108 |
0,9897 |
0,3153 |
0,1687 |
1,0000 |
0,3913 |
0,0148 |
|
Т2-2 |
0,2617 |
0,8969 |
0,2683 |
0,9952 |
0,9673 |
0,3913 |
1,0000 |
0,9033 |
|
Т2-3 |
-0,1208 |
0,9950 |
-0,1041 |
0,9359 |
0,9801 |
0,0148 |
0,9033 |
1,0000 |
Данная зависимость позволяет использовать полученные коэффициенты, к примеру, по алгоритму голосования, для диагностики измерительных каналов, сгруппировав модели следующим образом:
· модели 1, 3, 6 для проверки исправности Твх., Тсекц.1-1, Тсекц.2-1;
· модели 2, 5, 8 для проверки исправности Твых., Тсекц.1-3, Тсекц.2-3;
· модели 4 и 7 для проверки исправности Тсекц.1-2, Тсекц.2-2.
Для диагностирования исправности средств измерений температуры, к примеру на входе в реактор, возможно рассчитать среднеквадратическую ошибку (СКО) относительно верхних срезов реактора:
![]()
Нормальная работа измерительного оборудования будет обусловлена коэффициентами корреляции, которые остаются в заданном, близком друг к другу диапазоне rТвх, Тсекц.1-1, Тсекц.2-1 = {1; 0,99; 0,98}, и СКО ![]() , которое не будет превышать и 2 % в данном примере. По такому же принципу возможна проверка всех остальных взаимопроверяемых параметров [8].
, которое не будет превышать и 2 % в данном примере. По такому же принципу возможна проверка всех остальных взаимопроверяемых параметров [8].
Полученные модели могут использоваться как для целей диагностики, так и для повышения точности прогнозирования ОЧ за счет использования различных инструментов верификации вычисленных значений.
Основой верификации являются классические методы проверки статистических гипотиз и использования частотной логики [7].
Для реализации метода моделирования РБ установки КР с повышением точности оценки используются результирующие данные моделей (ОЧ). Которые группируются по временным срезам (всего 30, даты проведения лабораторных измерений) и разбиваются на две выборки — «обучающую» (20 временных срезов) и «тестирующую» (10 временных срезов соответственно). По их результатам строится одна эквивалентная модель с улучшенной точностью.
Цель применения независимой тестовой выборки — проверить, как обученная модель будет работать с новыми данными, т. е. приобрела ли она способность к обобщению.
В ходе построения обучающей и тестирующей выборок были найдены СКО относительно результата лабораторного измерения ОЧ и результатов полученных при моделировании. Построение обучающей выборки было обусловлено только нормированной СКО, которая рассчитывалась для каждой модели (всего 9) во всех временных срезах:
![]()
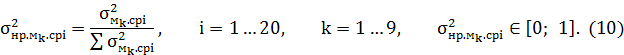
В результате полученная обучающая модель имеет вид:

Для построения независимых от результата измерения тестовых выборок применяется два подхода к их получению:
· в первом, тестовые выборки были получены путем «взвешивания» полученной ранее нормальной СКО. Данный подход позволяет использовать независимые от измерений весовые коэффициенты, отражающие отношение к лабораторному результату, чему соответствует убывающая ошибка и возрастающая величина весового коэффициента (и наоборот — ошибка возрастает, уменьшается вес).
Полученная эквивалентная модель с улучшенной точностью имеет следующий вид:


· во втором, тестовые выборки получаются путем распределения «рейтинга» (![]() ) среди моделей, по принципу — наиболее точная имеет больший рейтинг (и наоборот — менее точная, меньший).
) среди моделей, по принципу — наиболее точная имеет больший рейтинг (и наоборот — менее точная, меньший).
Полученная эквивалентная модель с улучшенной точностью имеет следующий вид:


Результатом аппроксимации применения данного метода стало увеличение точности относительно самой лучшей, из полученных ранее моделей, при первом подходе — на 3 %, а в среднем на 6,3 %. Применяя второй подход при моделировании, результаты следующие — относительно лучшей, точность была повышена на 5,3 % и в среднем на 8,5 % (рисунок 4) [2, 3].
В работе рассматриваются технические и алгоритмические аспекты решения задач получения моделей, разработки диагностических процедур и методов уточнения вычисленных значений ОЧ.
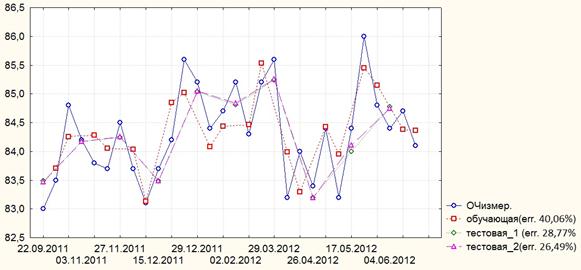
Рисунок 4. Результаты аппроксимации обучающей и тестовых моделей
Список литературы:
1.Ахметов С.А., Ишмияров М.Х., Веревкин А.П. и др. Технология, экономика и автоматизация процессов переработки нефти и газа: учеб. пособие. М.: Химия, 2005. 736 с.
2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике М.: Высш. школа, 1979, 400 стр.
3.Гмурман В. Е. Тория Вероятностей и Математическая Статистика 9-е изд., стер. — М.: Высшая школа, 2003. — 479 с.
4.Горицкий Ю.А., Перцов Е.Е. Практикум по статистике с пакетами StatGraphics, Statistica, SPSS.
5.Кафаров В.В., Мешалкин В.П., Грун Г., Нойманн В. Обеспечение и методы оптимизации надежности химических и нефтеперерабатывающих производств. М.: Химия, 1987. 272 с.
6.Куликов Г.Г., Брейкин Т.В., Камалова Л.З. Интеллектуальные информационные системы: Учеб. Пособие/ уфимск. гос. авиац. техн. ун-т. — Уфа, 1999. — 129 с.
7.Зверев Г.Н. Частотная логика — альтернатива классической логики в новых информационных.
8.Логические аппроксимации, лапласовы оценки и корреляционная логика Журн. «Информационные технологии» № 2, 1999. — С. 35—40.
дипломов


Оставить комментарий