БЫСТРОДЕЙСТВУЮЩИЙ  МЕТОД  КВАНТОВОХИМИЧЕСКИХ  РАСЧЕТОВ  С  АППРОКСИМАЦИЕЙ  ФОКИАНА  DFT  ДЛЯ  МАТЕМАТИЧЕСКОГО  МОДЕЛИРОВАНИЯ  ЭЛЕКТРОННОГО  СТРОЕНИЯ  БОЛЬШИХ  МОЛЕКУЛ

Аникин  Николай  Алексеевич

канд.  хим.  наук,  научный  сотрудник  ИОХ  РАН,  г.  Москва

E-mail:  nikan@swf.chem.ac.ru

Бугаенко  Владислав  Ленарович

канд.  хим.  наук,  старший  научный  сотрудник  ГНЦ  РФ  ИТЭФ,  г.  Москва

E-mail:  bugaenko@itep.ru

Кузьминский  Михаил  Борисович

канд.  хим.  наук,  старший  научный  сотрудник  ИОХ  РАН,  г.  Москва

E-mail: 

Мендкович  Андрей  Семёнович

д-р  хим.  наук,  руководитель  лаборатории  ИОХ  РАН,  г.  Москва

E-mail:  asm@free.net

Введение

В  работе  предложен  новый  метод  квантовохимических  расчетов  электронной  структуры  больших  молекул  с  быстродействием  на  уровне  быстрых  но  менее  точных  полуэмпирических  методов  и  точностью,  приближенной  к  популярным  более  точным  и  надежным  методам  функционала  электронной  плотности  (DFT,  Density  Functional  Theory).

Предложенный  квантовохимический  метод  NESE  (“Non  Empirized  Semi  Empirics”)  [1,  2,  3]  использует  «моделирование»  (аппроксимацию)  фокиана  метода  DFT.  В  данной  работе  рассматривается  начальная  неитерационная  версия  метода  —  NESE-0.  Она  включает  оператор  кинетической  энергии  плюс  сумму  атомных  потенциалов  с  эмпирическими  параметрами,  откалиброванными  по  МНК  из  отклонения  от  эталонного  одноэлектронного  фокиана  DFT.  Далее  предполагается  и  количественно  и  качественно  ее  усовершенствовать,  в  том  числе  —  вводя  итерации  метода  самосогласованного  поля  (ССП).  Работа  поддержана  РФФИ,  проект  11-07-00470.

Численные  результаты.

Метод  апробирован  на  молекулярных  системах  с  атомами  H,  C,  N,  O  с  параметрами,  подобранными  нами  по  DFT-расчетам  многих  тысяч  разнообразных  органических  молекул  с  типичных  группировками  этих  атомов.  Метод  сопоставлен  как  с  распространенными  полуэмпирическими  методами  AM1  [4],  наиболее  распространенным  PM3  [6],  и  новейшим  PM6  [7],  так  и  с  модельным  методом  DFT  (DFTB)  [8],  включенным  в  состав  известного  широко  употребляемого  квантовохимического  пакета  программ  Gaussian-09  [5].

Найдено  (см.  Рис.  1,  2,  3,  4),  что  радиальные  функции  атомных  потенциалов  NESE-0,  как  и  должно  быть,  убывают  с  ростом  расстояния  от  ядра,  особенно  резко  —  за  пределами  валентных  контактов,  приближаясь  к  нулю:  у  атома  Н  —  после  ~1,5  А,  у  атомов  C,  N,  O  —  после  ~  2  A.  Кривые  для  атомов  водорода  и  углерода  весьма  близки  для  трех  наборов  молекул:  углеводородного  набора  (только  атомы  H,  C)  ,  кислородсодержащего  набора  (атомы  H,  C,  O)  и  азотсодержащего  набора  (атомы  H,  C,  N),  что  свидетельствует  о  неплохой  переносимости  параметров  и  полезно  для  дальнейших  применений  метода.

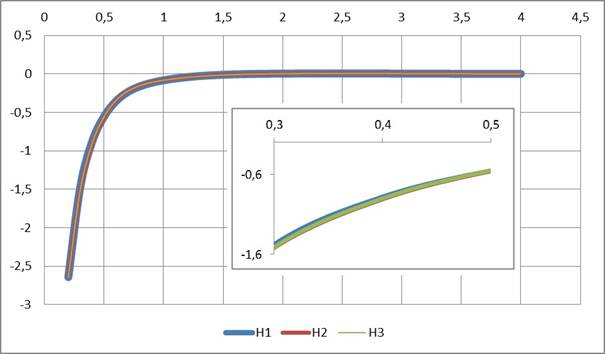
Рисунок  1.  Потенциал  атома  водорода:  H1  —  оптимизированного  по  молекулам  с  атомами  C,H;  H2  —  оптимизированного  по  молекулам  с  атомами  C,H,O;  H3  —  оптимизированного  по  молекулам  с  атомами  C,H,N

Рисунок  2.  Потенциал  атома  углерода:  C1  —  оптимизированного  по  молекулам  с  атомами  C,H;  C2  —  оптимизированного  по  молекулам  с  атомами  C,H,O;  C3  —  оптимизированного  по  молекулам  с  атомами  C,H,N

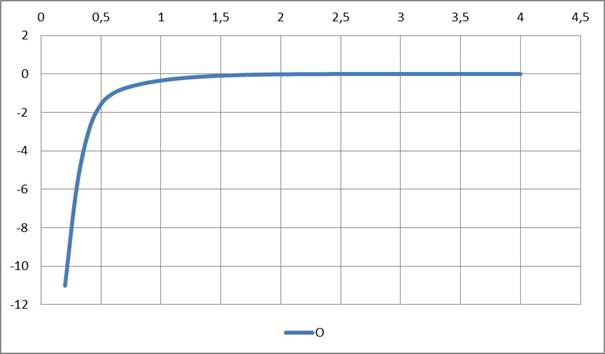
Рисунок  3.  Потенциал  атома  кислорода

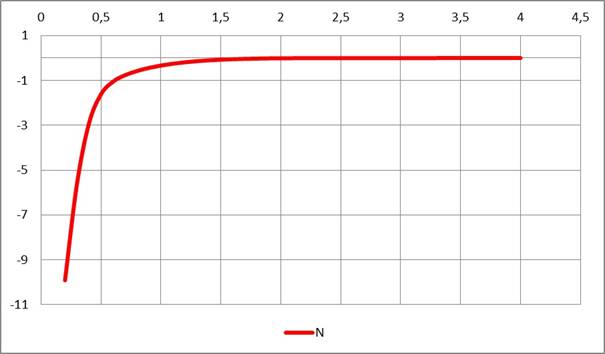
Рисунок  4.  Потенциал  атома  азота

Найдено,  что  уже  нынешняя  неитерационная  версия  NESE-0  предлагаемого  метода  кардинально  (по  порядку  величины)  точнее  итерационных  полуэмпирических  методов  (AM1,  PM3,  PM6)  воспроизводит  орбитальные  энергии  валентных  уровней  эталонного  метода  DFT  (функционал  PBE  в  базисе  MINI,  PBE/MINI),  и  превосходит  точность  (хотя  и  не  столь  кардинально)  итерационного  метода  DFTB,  особенно  по  зазору  между  верхними  занятыми  и  нижними  вакантными  МО,  что  особенно  важно  при  рассмотрении  вариации  (возмущении)  электронной  структуры  молекул.  Превосходство  предлагаемого  метода  NESE-0  носит  систематический  характер.

Углеводородные  молекулы.

Например,  на  2960  молекулах  углеводородов  (включая  сложные  пи-сопряженные  и  полициклические)  отклонение  от  эталонного  DFT  составило:

·у  предлагаемого  неитерационного  метода  NESE-0:  RMS  0,026308  a.  e.,  средняя  величина  отклонения  (в  одну  сторону)  —  0,010155  a.  e.,  максимальное  отклонение  0,131486  a.  e.;

·у  итерационного  полуэмпирического  метода  AM1:  RMS  0,27485,  среднее  одностороннее  —  0,22987  ,  максимальное  отклонение  0,92797  a.  e.;

·у  итерационного  полуэмпирического  метода  PM3:  RMS  0,27212  a.  e.,  среднее  одностороннее  —  0,23066,  максимальное  отклонение  0,90352  a.  e.;

·у  итерационного  полуэмпирического  метода  PM6:  RMS  0,21552  a.  e.  среднее  одностороннее  —  0,18706,  максимальное  отклонение  0,91536  a.  e.;

·у  итерационного  метода  DFTBa,  моделирующего  DFT:  RMS  0,12349  a.  e,  среднее  одностороннее  0,05672,  максимальное  отклонение  1,32266  a.  e.

Точность  (RMS)  описания  HOMO  (верхних  занятых  МО):  NESE-0:  0,026105,  AM1:  0,13465,  PM3:  0,13982,  PM6:  0,13263,  DFTBa:  0,01563  a.  e.

Точность  (RMS)  LUMO  (нижних  вакантных  МО):  NESE-0:  0,026525,  AM1:  0,07643,  PM3:  0,07934,  PM6:  0,07016,  DFTBa:  0,03223  a.  e.

Точность  (RMS)  зазора  между  LUMO  и  HOMO:  NESE-0:  0,011641,  AM1:  0,14995,  PM3:  0,14843,  PM6:  0,15091,  DFTBa:  0,02046  a.  e.

Видно,  что  точность  предлагаемого  неитерационного  метода  NESE-0  примерно  в  10  раз  превышает  точность  полуэмпирических  методов  (AM1,  PM3,  PM6),  которые  в  среднем  мало  отличаются  друг  от  друга  (хотя  на  отдельных  молекулах  они  отличаются  значительно).  По  сравнению  с  итерационным  метода  DFTBa,  моделирующего  DFT,  NESE-0  выигрывает  меньше,  в  2—4  раза.

Точность  довольно  равномерна  по  разным  группам  данного  класса  молекул.  Так,  для  715  разнообразных  молекул  алкенов  и  полиенов,  включая  циклические,  отклонение  от  эталонного  DFT  составило:

·у  предлагаемого  метода  NESE-0:  RMS  0,022544  a.  e.  (у  алканов  и  циклоалканов  средняя  величина  RMS  была  0,014931  a.  e.),  отклонения  (в  одну  сторону)  —  0,010189,  максимальное  отклонение  0,095188  a.  e.;

·у  метода  AM1:  RMS  0,26871,  среднее  в  одну  сторону  —  0,23201,  максимальное  отклонение  0,68863  a.  e.;

·у  метода  PM3:  RMS  0,27049  a.  e.,  среднее  в  одну  сторону  —  0,18813,  максимальное  отклонение  0,78107  a.  e.;

·у  метода  PM6:  RMS  0,20756  a.  e.  среднее  одностороннее  —  0,18706,  максимальное  отклонение  0,67538  a.  e.;

·у  метода  DFTBa,  моделирующего  DFT:  RMS  0,08477  a.  e.,  среднее  одностороннее  0,03585,  максимальное  отклонение  0,70856  a.  e.

Точность  зазора  LUMO-HOMO:  NESE-0:  0,006406,  AM1:  0,17550,  PM3:  0,17278,  PM6:  0,17743,  DFTBa:  0,02059  a.  e.

Здесь  также  выигрыш  NESE-0  у  полуэмпирических  методов  на  порядок,  а  у  DFTB  —  в  2—4  раза.

Кислородсодержащие  молекулы.

Точность  на  2846  сложных  и  разнообразных  молекулах  с  атомами  углерода,  водорода  и  кислорода  (включая  гликозиды  и  т.  д.)  составила:

·у  предлагаемого  метода  NESE-0:  RMS  0,022926  a.  e.,  средняя  величина  отклонения  —  0,007262,  максимальное  отклонение  0,133307  a.  e.;

·у  метода  AM1:  RMS  0,27045,  среднее  одностороннее  —  0,23113,  максимальное  отклонение  0,92101  a.  e.;

·у  метода  PM3:  RMS  0,26505,  среднее  одностороннее  —  0,22945,  максимальное  отклонение  0,90282  a.  e.;

·у  метода:  RMS  0,21397,  среднее  одностороннее  —  0,19098,  максимальное  отклонение  0,90858  a.  e.;

·у  метода  DFTBa:  RMS  0,12029  a.  e.,  среднее  одностороннее  0,06000,  максимальное  отклонение  1,32266  a.  e.

Точность  зазора  LUMO-HOMO:  NESE-0:  0,017913,  AM1:  0,18242,  PM3:  0,18155,  PM6:  0,17022,  DFTBa:  0,06288  a.  e.

Точность  близка  в  точности  для  углеводородов,  в  среднем  немного  больше  погрешность  зазора  LUMO-HOMO,  что  естественно  ввиду  значительной  полярности  связей  C-O  и  O-H.

Азотсодержащие  молекулы.

Точность  на  2035  сложных  и  разнообразных  молекулах  с  атомами  углерода,  водорода  и  азота  (включая  пи-сопряженные  гетероциклы)  составила:

·у  предлагаемого  метода  NESE-0:  RMS  0,026409  a.  e.,  среднее  одностороннее  отклонение  —  0,009705,  максимальное  отклонение  0,129880  a.  e.;

·у  метода  AM1:  RMS  0,27178,  среднее  одностороннее  —  0,22832,  максимальное  отклонение  0,92101  a.  e.;

·у  метода  PM3:  RMS  0,26505,  среднее  одностороннее  —  0,22591,  максимальное  отклонение  0,90282  a.  e.;

·у  метода  PM6:  RMS  0,21574,  среднее  одностороннее  —  0,18849,  максимальное  отклонение  0,90858  a.  e.;

·у  метода  DFTBa:  RMS  0,12853  a.  e.,  среднее  одностороннее  0,06298,  максимальное  отклонение  1,27607  a.  e.

Точность  (RMS)  зазора  LUMO-HOMO:  NESE-0:  0,019456,  AM1:  0,17202,  PM3:  0,16629,  PM6:  0,16892,  DFTBa:  0,02876  a.  e.

Точность  близка  к  точности  предыдущих  групп.

Обсуждение.

В  дальнейшем  предложенный  метод  NESE-0  предполагается  усовершенствовать  за  счет  неитерационного  учета  влияния  окружения  данного  атома  на  его  потенциал  и  учета  анизотропии  потенциала  атома  (это  было  особенно  видно  на  полиацетиленах,  где  сильна  анизотропия  вдоль  цепи  атомов  углерода).  Этот  неитерационный  метод  (в  усовершенствованной  версии)  может  быть  полезен:

·для  расчетов  мало  полярных  органических  молекул  или  молекул  с  изолированными  полярными  связями  без  их  включения  в  цепь  пи-сопряжения  (успешность  этого  продемонстрирована  на  кислород-  и  азот-содержащих  молекулах);

·как  хорошее  начальное  приближение  для  итерационных  методов  с  любым  заданным  функционалом  DFT;

·в  методах  класса  QM/QM  с  заданным  функционалом  DFT,  где  будет  отсутствовать  резкое  отличие  методов  (например,  NESE-0/PBE),  так  как  NESE-0  как  раз  и  моделирует  данный  функционал  DFT.

Также  предполагается  сооружение  итерационной  версии  NESE,  но  при  сохранении  экономичности  метода  на  уровне  DFTB  и  близко  к  полуэмпирическим  методам.

Выводы.

Предложенный  принципиально  новый  метод  NESE  (“Non  Empirized  Semi  Empirics”),  моделирующий  расчеты  точными,  но  ресурсоемкими  методами  DFT;  определены  пути  его  дальнейшего  развития.

Результаты  апробации  начальной  версии  метода  NESE-0  на  многих  тысячах  разнообразных  органических  молекул  содержащих  атомы  C,  H,  N,  O,  показывают,  что  даже  эта  начальная  несовершенная  и  неитерационная  версия  метода  по  точности  моделирования  фокиана  (Гамильтониана)  DFT  умеренно  превосходит  итерационный  метод  DFTB,  моделирующий  DFT,  и  на  порядок  —  итерационные  полуэмпирические  методы  AM1,  PM3,  PM6  (известные  методы  сходного  уровня  ресурсоемкости).

Использование  метода  NESE,  в  том  числе  и  в  комбинации  с  базовыми  методами  DFT,  может  быть  актуально  для  проведения  массовых  расчетов  больших  молекул  (наноструктур  и  биомолекул),  в  т.  ч.  для  задач  конструирования  лекарственных  средств,  где  применение  DFT  приводит  к  недопустимо  высоким  затратам  вычислительных  ресурсов,  а  полуэмпирические  методы  не  могут  быть  использованы  из-за  недостаточной  точности  и  надежности.

Список  литературы:

1.Аникин  Н.А.,  Кузьминский  М.Б.  Новая  аппроксимация  DFT  для  быстрых  расчетов  био-  и  наноструктур  //  Информационно-вычислительные  технологии  в  науке  —  2011,  Сб.  тезисов.  —  М.:  2011  —  С.  29—30.

2.Anikin  N.A.,  Bugaenko  V.L.,  Anisimov  V.M.  Chemically  parameterized  fast  DFT  method  //  225th  ACS  National  Meeting  (New  Orleans)/COMP  /  Computers  in  Chemistry.  P.  243.

3.Anikin  N.A.,  Bugaenko  V.L.,  Anisimov  V.M.  Semi-DFT  approach  to  calculation  of  protein  systems  //  226th  ACS  National  Meeting  (New  York,  Fall  2003)/COMP  /  Computers  in  Chemistry.  P.  112.

4.Dewar  M.J.S.,  Zoebisch  E.G.,  Healy  E.F.,  Stewart  J.J.P.  Development  and  use  of  quantum  mechanical  molecular  models.  76.  AM1:  A  new  general  purpose  quantum  mechanical  molecular  model  //  J.  Am.  Chem.  Soc.  1985.  Vol.  107.  №  13.  P.  3902—3909.

5.Frisch  M.J.,  Trucks  G.W.,  Schlegel  H.B.,  e.  a.  Gaussian  09,  Revision  A.02  //  Gaussian,  Inc.,  Wallingford  CT.  2009.

6.Stewart  J.J.P.  Optimization  of  parameters  for  semiempirical  methods  I.  Method  //  J.  Comput.  Chemistry.  1989.  Vol.  10.  №  2.  P.  209—220.

7.Stewart  J.J.P.  Optimization  of  Parameters  for  Semiempirical  Methods  V:  Modification  of  NDDO  Approximations  and  Application  to  70  Elements  //  J.  Molec.  Modeling.  2007.  Vol.  13.  №  12.  P.  1173—1213.

8.Zheng  G.,  Lundberg  M.,  Jakowski  J.,  Vreven  T.,  Frisch  M.J.,  Morokuma  K.  Implementation  and  benchmark  tests  of  the  DFTB  method  and  its  application  in  the  ONIOM  method  //  Int.  J.  Quant.  Chem.  2009.  Vol.  109.  №  9.  P.  1841—1854.