АЭРОДИНАМИЧЕСКИЕ  ХАРАКТЕРИСТИКИ  СПУСКАЕМОГО  АППАРАТА  В  РАЗРЕЖЕННОМ  ГАЗЕ

Зея  Мьо  Мьинт

канд.  физ.-мат.  наук,  докторант  МФТИ,  г.  Жуковский

E-mail:  zayyarmyomyint@gmail.com

Хлопков  Антон  Юрьевич

аспирант  МФТИ,  г.  Жуковский

E-mail: 

Чжо  Зин

аспирант  МФТИ,  г.  Жуковский

E-mail: 

Освоение  околоземного  пространства  на  современном  этапе  требует  разработки  воздушно-космических  систем,  пригодных  для  оперирования  в  космическом  пространстве  и  в  верхних  слоях  атмосферы.  Под  перспективными  летательными  аппаратами  понимаются  многоразовые  возвращаемые  летательные  аппараты,  способные  осуществлять  управляемый  планирующий  спуск  в  верхних  слоях  атмосферы  [1,  5].

Целью  настоящей  работы  является  определение  основных  аэродинамических  характеристик  (АДХ)  спускаемого  аппарата  в  высокоскоростном  потоке  разреженного  газа.  Задача  нахождения  АДХ  тела  заключается  в  нахождении  при  заданных  характеристиках  падающих  и  отраженных  молекул  безразмерных  коэффициентов  сил  и  моментов

  .

Представлены  результаты  определения  аэродинамических  характеристик  спускаемого  аппарата  при  его  обтекании  гиперзвуковым  разреженным  потоком  в  рамках  метода  Монте-Карло  и  локального  метода  [2,  3].  Используются  различные  модели  взаимодействия  молекул  с  поверхностью.  Значения  параметров:  температурный  фактор  t_w  =  T_w/T_¥  =  0.04;  скоростное  отношение  s  =  20;  коэффициенты  аккомодации  тангенциального  импульса  и  нормальной  энергии  σ_τ  ,  σ_n  =  0.5,  1;  угол  атаки  a  =  0°—30°.

Представлены  результаты  расчета  различным  моделями  взаимодействия  газа  с  поверхностью  Максвелла  и  Черчиньяни-Лампис-Лорда  (CLL).  Можно  объяснить  что,  при  нулевой  аккомодации  все  молекулы  отражаются  зеркально,  и  полной  аккомодации  отражаются  диффузно.  Зеркальные  отраженные  молекулы  передают  поверхности  больший  импульс,  чем  диффузно  рассеянные  от  холодной  стенки  молекулы  [4].  Можно  объяснить  что,  величина  нормальных  и  касательных  напряжений,  вызываемых  отраженным  потоком,  зависит  от  характера  отражения  молекул.  При  зеркальном  отражении  p_r  =  p_i.  Тогда  суммарное  нормальное  напряжение,  действующее  на  элемент  поверхности,  будет  равно  p  =  2p_i.  При  диффузном  отражении  касательное  напряжение  от  отраженных  молекул  равно  нулю,  так  как  при  этом  все  направления  отражения  являются  одинаково  вероятными. 

Рисунок  1.  Геометрический  вид  спускаемого  аппарата

На  рис.  2—4  представлены  зависимости  коэффициентов  силы  сопротивления  C_x  и  подъемной  силы  C_y,  моменты  тангажа  M_z  от  углах  атаки  α  при  различных  σ_τ  для  спускаемого  аппарата  (рис.  1). 

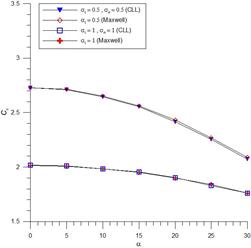
Рисунок  2.  Зависимости  C_x(a)  при  t_w  =  0,04

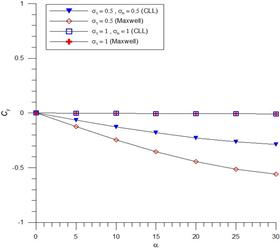
Рисунок  3.  Зависимости  C_y(a)  при  t_w  =  0,04

Рисунок  4.  Зависимости  M_z(a)  при  t_w  =  0,04

C_x  уменьшается  с  ростом  угла  атаки  до  значения  около  1,89  при  α  =  30°  при  σ_τ  =  1.  При  уменьшении  σ_τ  от  1  до  0,5  величина  C_x  увеличивается  до  2,72  при  α  =  0°.  Коэффициент  C_y  снижает  в  несколько  раз  по  модулю  при  уменьшении  σ_τ  от  1  до  0,5.  Зависимость  M_z(a)  объясняет  о  том,  что  при  понижении  σ_τ  чувствительно  увеличивает  в  рамках  разных  диапазонов  углов  атаки.

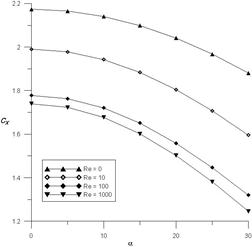
Рисунок  5.  Зависимости  C_x(a)  при  Re  =  0,  10,  100,  1000  (t_w  =  0,04)

Рисунок  6.  Зависимости  C_y(a)  при  Re  =  0,  10,  100,  1000  (t_w  =  0,04)

На  рис.  5—7  представлены  зависимости  C_x(a),  C_y(a),  M_z(a)  для  спускаемого  аппарата  на  различных  этапах  траектории,  в  частности,  при  различных  числах  Рейнольдса  Re. 

Рисунок  7.  Зависимости  M_z(a)  при  Re  =  0,  10,  100,  1000  (t_w  =  0,04)

Программа  и  результаты  смогут  быть  полезны  для  многопараметрических  вычислений  при  создании  современных  перспективных  космических  аппаратов.  Работа  выполнена  при  поддержке  РФФИ  (Грант  №  11-07-00300-а).

Список  литературы:

1.Белоцерковский  О.М.,  Хлопков  Ю.И.  Методы  Монте-Карло  в  механике  жидкости  и  газа.  —  М.:  Азбука,  2008.  —  330  с. 

2.Галкин  В.С.,  Ерофеев  А.И.,  Толстых  А.И.  Приближенный  метод  расчета  аэродинамических  характеристик  тел  в  гиперзвуковом  разреженном  газе  //  Труды  ЦАГИ.  1977.  Вып.  1833.

3Зея  Мьо  Мьинт,  Хлопков  А.Ю.  Аэродинамические  характеристики  летательного  аппарата  сложной  формы  с  учётом  потенциала  взаимодействия  молекулярного  потока  с  поверхностью//  Ученые  записки  ЦАГИ.  —  2010.  —  Т.  XLI.  —  №  5.  —  с.  33—45.

4.Коган  М.Н.  Динамика  разреженного  газа.  —  М.:  Наука,  1967.

5.Хлопков  Ю.И.  Статистическое  моделирование  в  вычислительной  аэродинамике.  —  М.:МФТИ,  2006.  —  260  с.