ИССЛЕДОВАНИЕ  АЭРОТЕРМОДИНАМИКИ  ПЕРСПЕКТИВНОГО  ВОЗДУШНО-КОСМИЧЕСКОГО  АППАРАТА

Хлопков  Юрий  Иванович

д-р  физ.-мат.  наук,  профессор  МФТИ,  г.  Жуковский

E-mail:  khlopkov@falt.ru

Зея  Мьо  Мьинт

канд.  физ.-мат.  наук,  докторант  МФТИ,  г.  Жуковский

E-mail:  zayyarmyomyint@gmail.com

Хлопков  Антон  Юрьевич

аспирант  МФТИ,  г.  Жуковский

E-mail:  khlopkov@falt.ru

Чжо  Зин

аспирант  МФТИ,  г.  Жуковский

E-mail: 

Актуальной  проблемой  аэрокосмической  техники  является  предсказание  аэротермодинамических  характеристик  летательных  аппаратов  вдоль  всей  траектории  —  от  орбитального  полета  до  посадочного  режима  [1,  5,  6].  Теоретический  расчет  характеристик  теплопередачи  тела  основывается  на  знании  законов  взаимодействия  молекул  газа  с  поверхностью.  В  качестве  граничного  условия,  накладываемого  на  плотность  распределения  отраженных  от  поверхности  молекул  газа,  часто  используют  зеркально-диффузную  модель  Максвелла  [4].  В  граничном  условии  Черчиньяни  [7]  скорости  отраженных  молекул  также  определяются  коэффициентом  аккомодации  тангенциального  импульса  σ_τ.  Более  гибкой  моделью  является  модель  Черчиньяни-Лампис  [8],  которая  позволяет  при  постановке  граничных  условий  учесть  коэффициент  аккомодации  тангенциального  импульса  σ_τ  и  коэффициент  аккомодации  нормальной  к  поверхности  кинетической  энергии  σ_n.  Моделью  Леннарда-Джонса  является  потенциал  взаимодействия  молекул,  использующий  электронно-ядерные  представления  [4].  Эмпирические  потенциальные  зависимости  отражают  тот  факт,  что  на  больших  расстояниях  преобладают  силы  притяжения,  на  малых  расстояниях  —  силы  отталкивания.

Представлены  результаты  определения  аэротермодинамических  характеристик  воздушно-космического  аппарата  «Клипер,  модель  ЦАГИ»  (рис.  1)  [3]  в  свободно-молекулярном  режиме  с  применением  различных  моделей.  В  частности,  рассматриваются  модели  Максвелла  (Maxwell),  Черчиньяни-Лампис-Лорда  (Cercignani-Lampis-Lord,  CLL)  и  Леннарда-Джонса  (Lennard-Jones,  LJ)  из  работ  [4,  12]. 

Рисунок  1.  Воздушно-космический  аппарат  «Клипер».  Общий  вид,  вычислительная  схема

В  свободно  молекулярном  случае  коэффициент  теплопередачи  на  элемент  поверхности

,

здесь    a_e  —  коэффициент  аккомодации  энергии  на  стенке,  s_¥,q  —  скоростное  отношение,  ориентированное  на  угол  q  T_w,  T_¥  —  температуры  стенки  и  набегающего  потока,  s_¥,q  =  s_¥  cos  q.

На  рис.  2,  3  представлены  зависимости  коэффициента  теплопередачи  потока  C_h  от  углах  атаки  α  для  различных  моделей  взаимодействия  молекул  газа  с  поверхностью.

Рисунок  2.  Зависимости  C_h(α)    при  σ_τ  =  0.9  и  1  Максвелла

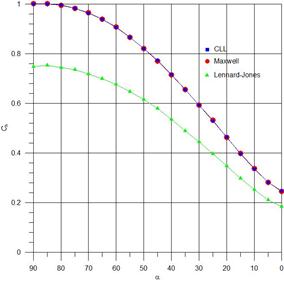
Рисунок  3.  Зависимости  C_h(α)  по  моделям  CLL  (σ_τ  ,  σ_n  =  1)  и  LJ

Модель  CLL  дает  более  высокое  значение  коэффициента  теплопередачи,  чем  модель  Максвелла,  при  том  же  коэффициенте  аккомодации  0.9.  На  рис.  3  представлены  зависимости  C_h(a)  с  использованием  различных  моделей  взаимодействия  молекул  с  поверхностью  (Максвелл,  CLL,  LJ).  Из  результатов  ясно,  что  модели  Максвелл  и  CLL  дают  одинаковые  значения  при  коэффициентах  аккомодации  равных  единице  (рис.  2). 

В  данной  работе  представлено  определение  локально-мостового  метода  для  вычисления  аэротермодинамики.  Для  вычисления  C_h  на  элементарную  площадку  в  свободномолекулярном  пределе  используются  аналитические  формулы,  написанные  в  [4]  и  для  вычисления  C_h  в  континуальном  режиме  будем  использовать  методику,  основанную  на  теории  Лии  [11].  Локально-мостовой  метод  позволяет  быстро  получить  аэротермодинамические  характеристики  в  переходном  режиме  [2,  10].

,

Здесь  q  —  угол  между  направлением  потока  и  нормалью  к  элементарной  площадке,  M  —  число  Маха,  Re  —  число  Рейнольдса,  S  —  площадь  поверхности  тела,  индекс  fm  означает  значения  параметров  при  свободно  молекулярном  обтекании.  Функция  F_b  называется  мостовой  функцией.  Рассмотрим  мостовую  функцию,  выражающуюся  как  функция  ошибки  от  логарифма  числа  Кнудсена:

Если  Kn₀  <  Kn_m,  используется  мостовая  функция  F_b,1.  В  противном  случае  F_b,2.  Значения  Kn_m  =  0.3,  ΔKn₁  =  1.3  и  ΔKn₂  =  1.4  были  определены  путем  сравнения  с  результатами  моделирования  методом  прямого  статистического  моделирования  (Монте-Карло).

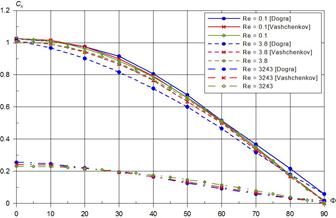
Рисунок  4.  Угловое  распределение  C_h  на  сфере.  Представлены  полученные  в  данной  работе  результаты  в  сравнение  с  экспериментальными  результатами  Dogra  V.K.,  Wilmoth  R.G.  [9]  и  расчетными  данными  Ващенкова  П.В.  [2]

На  рис.  4  показаны  результаты  расчета  зависимости  C_h  на  поверхности  сферы  от  угла  при  различных  числах  Рейнольдса  с  помощью  локально-мостового  метода.  На  графике  видно,  что  сравнение  результатов  теплового  потока  в  континуальном  и  свободномолекулярном  режиме  определенные  локально-мостовым  методом  хорошо  совпадают.  В  переходном  режиме  дает  завышенное  значение  коэффициента  теплопередачи  примерно  на  15  %  на  углах  20—50  градусов.  Работа  выполнена  при  поддержке  РФФИ  (Грант  №  11-07-00300-а).

Список  литературы:

1.Белоцерковский  О.М.,  Хлопков  Ю.И.  Методы  Монте-Карло  в  механике  жидкости  и  газа.  —  М.:  Азбука,  2008.  330  с.

2.Ващенков  П.В.  Численный  анализ  высотной  аэротермодинамики  космических  аппаратов  //  Дис.  канд.  тех.  наук,  ИТПМ  СО  РАН,  —  Новосибирск,  —  2012. 

3.Зея  Мьо  Мьинт,  Хлопков  А.Ю.  Аэродинамические  характеристики  летательного  аппарата  сложной  формы  с  учётом  потенциала  взаимодействия  молекулярного  потока  с  поверхностью//  Ученые  записки  ЦАГИ.  —  2010.  —  Т.  XLI.  —  №  5.  —  с.  33—45.

4.Коган  М.Н.  Динамика  разреженного  газа.  Кинетическая  теория.  —  М.:  Наука.  —  1967.  —  440  с. 

5.Хлопков  Ю.И.  Статистическое  моделирование  в  вычислительной  аэродинамике.  —  М.:МФТИ,  2006.  —  260  с.

6.Belotserkovskii  O.M.,  Khlopkov  Y.I.  Monte  Carlo  Methods  in  Mechanics  of  Fluid  and  Gas.  World  Scientific  Publishing  Co.  N-Y,  London,  Singapore,  Beijing,  Hong  Kong.  —  2010.  —  268  p. 

7.Cercignani  C.  The  Kramers  Problem  for  a  not  Complete  Diffusing  Wall  //  J.  Math.  Phys.  Appl.  —  1965.  —  V.  1.  —  №  3.  —  P.  568—586. 

8.Cercignani  C.,  Lampis  M.  Kinetic  Models  for  Gas-Surface  Interactions  //  Transport  Theory  and  Statistical  Physics.  —  1971.  —  V.  1.  —  №  2.  —  P.  101—114. 

9.Dogra  V.K.,  Wilmoth  R.G.,  Moss  J.N.  Aerothermodynamics  of  1.6  -m-  diameter  sphere  in  Hypersonic  Rarefied  Flow.  J.  AIAA.  —  1992.  —  Vol.  30.  —  №  7.  —  pp.  1789—1794.

10.Ivanov  M.S.,  Markelov  G.N.,  Gimelshein  S.F.,  Mishina  L.V.,  Krylov  A.N.,  Grechko  N.V.  High-Altitude  Capsule  Aerodynamics  with  real  gas  effects,  —  J.  of  Spacecraft  and  Rocket,  —  1998.  —  Vol.  35.  —  №  1.  —  pp.  16—22.

11.Lee  Lester  Laminar  heat  transfer  over  blunt  nosed  bodies  at  hypersonic  flight  speeds  //  Jet  Propulsion.  —  1956.  —  Vol.  26.  —  №  4.  —  pp.  259—269.

12.Padilla  J.F.  Assessment  of  Gas-Surface  Interaction  Models  for  Computation  of  Rarefied  Hypersonic  Flows  //  Ph.D.  Dissertation.  —  University  of  Michigan,  2008.