ВОЗМОЖНЫЕ  СПОСОБЫ  ЗАЩИТЫ  ИНФОРМАЦИИ  ОТ  ПЕРЕДАЧИ  ДАННЫХ  ПО  СКРЫТОМУ  КАНАЛУ  В  СИСТЕМАХ  ЭЛЕКТРОННОЙ  ЦИФРОВОЙ  ПОДПИСИ

Куржеевский  Игорь  Владимирович

старший  преподаватель

Бродовская  Виолетта  Владимировна

студент

Папкова  Анна  Станиславовна

студент

Шумкова  Алина  Андреевна

студент  Академия  военно-морских  сил  имени  П.С.  Нахимова,  Севастопольский  национальный  технический  университет  г.  Севастополь

E-mail:  violetta94@yandex.ru

В  вычислительных  сетях  возможно  создание  скрытого  канала  передачи  данных  при  использовании  алгоритмов  электронной  цифровой  подписи  (ЭЦП).  Скрытый  канал  —  непредусмотренный  разработчиком  коммуникационный  канал,  по  которому  могут  быть  переданы  сообщения.  Впервые  концепцию  создания  скрытого  канала  предложил  Г.  Симмонс,  на  основе  криптограмм,  внедряя  в  них  дополнительную  информацию.  Описанные  им  алгоритмы,  опираются  на  свойства  операций  в  кольце,  и  подмену  генерируемого  случайного  числа.  Был  приведен  «типичный»  протокол  скрытого  канала:  отправитель,  используя  секретный  ключ,  общий  с  получателем,  подписывает  невинное  сообщение,  пряча  в  подписи  скрытое  сообщение,  создавая  скрытый  канал  с  помощью  обычных  алгоритмов  цифровой  подписи  [5;  4].

Допустим,  для  реализации  скрытого  канала  связи  абоненты  A  и  B  обмениваются  секретными  сообщениями,  и  не  хотят,  чтобы  кто-либо  узнал  их  содержание.  В  таком  случае  A  и  B  могут  просто  шифровать  свои  сообщения  с  помощью  симметричной  или  асимметричной  криптосистемы.  Но  что,  если  некоторая  проверяющая  сторона  С,  облеченная  властью,  может  заставить  A  и  B  открыть  свои  ключи  и,  тем  самым,  прочитать  содержание  посланных  писем  [3].  Тогда  абоненту  А  и  В  стоит  передавать  свои  сообщения  по  скрытому  каналу  связи.  Абонент  A,  желая  отправить  абоненту  B  тайное  послание,  берет  некоторый  электронный  документ,  подписывает  его  цифровой  подписью,  встроив  в  нее  тайное  сообщение  (послание)  и  отправляет  по  открытому  каналу  связи.  Проверяющая  сторона  С  перехватив  сообщение,  проверяет  подпись  под  ним,  и,  не  встретив  ничего  подозрительного,  успокаивается.  Абонент  B,  получив  послание,  выбрасывает  обычное  сообщение  и  извлекает  из  подписи  тайное  послание.

Примерами  этого  могут  быть  ЭЦП  на  основе  Онга-Шнорра-Шамира  и  Эль-Гамая:

              I. Для  реализации  скрытого  канала  связи  на  основе  ЭЦП  Онга-Шнорра-Шамира,  абонент  А  создает  несекретное  электронное  цифровое  письмо,  которое  подписывает  своей  ЭЦП.  Рассмотрим  алгоритм  создания  скрытого  канала  передачи  данных:

1.  Необходимо  сгенерировать  простое  число  p.

p:=20965_57522_55599_48381_65640_12682_89294_80366_27757_04125_85321.

2.  Необходимо  сгенерировать  простое  число  q.

q:=524_13938_06389_98709_54141_00317_07232_37009_15693_92603_14633.

3.  Найдем  произведение  простых  чисел  p  и  q,

4.   

;

n=109_88883_61346_53270_11519_55309_94082_21433_82869_49067_30074_98751_09077_70284_21779_75910_

88737_35685_76934_77622_54173_02193.

5.       Абонент  А  выбирает  случайное  число  k  взаимно  простое  с  числом  n  (k,n)=1  в  качестве  секретного  ключа,  и  безопасным  образом  передает  абоненту  B.  k=101_38471_35900_09972_41845_07521_12418_54002_29300_24391_39080_52433_88030_17857_85033_54028_57616_

38594_50522_62960_45698_08558.

6.  Вычисляем  открытый  ключ  ЭЦП  по  формуле:

;

h=106_87870_09061_52833_61191_83933_52053_17318_65530_00604_35905_82962_46703_49048_65535_67486_

08392_19351_49936_28845_03235_29065.

7.  Находим  M  —  хэш-значение  документа.

M:=1382_84847_09165_00511_11918_70517_30116_45583_99521_29616.

8.  Скрытое  сообщение,  (например:  «Явка  провалена  Петров  предатель,  связь  по  запасному  каналу.»),  зашифровываем  в  виде  числа  r.

r=33341_20134_17181_60301_13061_50134_17062_01816_03341_71806_05012_00613_28341_90333.

9.  Вычисляем  первую  часть  ЭЦП,  по  формуле:

S₁=108_26089_00102_01367_24697_41536_81577_31147_90246_28873_59350_68774_71930_68760_78681_63442_

25996_57098_18051_47207_25418_03135.

10.                Вычисляем  вторую  часть  ЭЦП,  по  формуле:

S₂=23_04330_44609_99093_36824_22900_31352_18910_36684_11661_84201_71445_01324_73699_70302_73771_

10316_37970_47167_31875_92211_25785.

11.                Проверка  подлинности  ЭЦП,  осуществляется  по  формуле:  .  Проверяющая  сторона  С  может  убедиться  в  том,  что  подпись  подлинная,  а  передаваемая  ЭЦП  и  подпись  к  нему  в  явном  виде  скрытой  информации  не  содержит.  Скрытую  информацию  можно  получить  путем  вычислений  по  следующей  формуле: 

 .

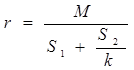Докажем,  что  эти  вычисления  позволяют  извлечь  скрытую  информацию.  Заменим  в  формуле  S₁  и  S₂.  Получим

скрытое  сообщение,  которое  расшифровываем  с  помощью  заранее  согласованного  между  абонентами  А  и  В  криптоалгоритма  с  известным  им  ключом.

           II.          Рассмотрим  организацию  скрытого  канала  на  основе  ЭЦП  Эль-Гамаля  с  составным  модулем,  основанной  на  сложности  решения  задачи  факторизации.  Применение  в  схемах  ЭЦП,  подобных  системе  Эль-Гамаля,  составного  модуля  вместо  простого  связано  с  тем,  что  большое  число  таких  схем  не  обеспечивает  стойкости  к  атакам,  основанным  на  вычислении  подписи  путем  подбора  параметра    в  виде  [2]  .  В  таких  атаках  требуется  знание  функции  Эйлера  от  модуля,  поэтому  они  могут  быть  устранены  применением  составного  модуля.

Ряд  возможных  схем  реализации  ЭЦП  с  составным  модулем  представлен  в  таблице  1  [2].

Таблица  1.

Варианты  ЭЦП  с  составным  модулем

где:    —  составной  модуль,  представляющий  собой  произведение  больших  простых  чисел    и  ; 

  —  хеш-значение  документа; 

  —  секретный  ключ; 

  —  открытый  ключ; 

  —  сгенерированное  большое  простое  число  размером  160—256  бит,  являющееся  делителем  больших  простых  чисел    и  ; 

  —  параметр,  который  содержит  секретное  сообщение; 

  —  наименьшее  число,  такое,  что  ;  параметр  ЭЦП  r  вычисляется  по  формуле:    [2];  пара  чисел  представляет  собой  ЭЦП  документа.

На  основе  предложенной  ЭЦП,  скрытый  канал  организовывается  следующим  образом.  Пусть  по  скрытому  каналу  необходимо  передать  конфиденциальное  сообщение  M:  «Акции  компании  Х  вырастут!».  Предварительно  абонент  А  и  В  договариваются  о  методе  шифрования  секретного  сообщения  M.  Cкрываемое  сообщение  подменяет  собой  число  ,  а  остальные  шаги  алгоритма  формирования  ЭЦП  не  изменяются.

Скрытой  информацией  передаваемого  электронного  документа  с  ЭЦП  служит  значение  параметра  :    =  1125522424253432351133242451133423411142434443.

На  подготовительном  этапе  формирования  подписи  абонент  А  выбирает  два  больших  простых  числа  и    и  перемножает  их,  получая  модуль: 

.  (1)

Значение    принимается  в  качестве  части  открытого  ключа  ,  а  значения  простых  множителей  держатся  в  секрете  или  уничтожаются  после  вычисления:

.  (2)

Абонент  А  выбирает  в  качестве  секретного  ключа    произвольное  число  меньшее  чем  n.  Это  число  используется  не  только  для  подписи  сообщения,  но  и  в  качестве  ключа  для  отправки  и  чтения  скрытого  сообщения.

Так  же  для  подписи  электронного  документа  используется  открытый  ключ  ,  вычисляемый  по  секретному  ключу  : 

.  (3)

Для  потенциального  нарушителя  в  уравнении  генерации  подписи  присутствуют  две  неизвестные  величины:    и  .  Поэтому  он  не  имеет  возможности  с  большой  вероятностью  вычислить  секретный  ключ  .

Длина  числа    может  быть  выбрана  сравнительно  небольшой  (меньше  размера  используемых  значений  и  );  число    должно  удовлетворять  следующему  уравнению: 

.  (4)

Абонент  А  подписывает  электронный  документ,  пряча  в  подписи  скрытое  сообщение  .  По  уравнению  формирования  подписи  из  схемы  1  абонентом  А  вычисляется    и  : 

,  (5)

.  (6)

Процедура  проверки  подлинности  электронного  документа,  подписанного  с  помощью  электронной  цифровой  подписи  с  составным  модулем,  происходит  следующим  образом.  У  получателя  есть  переданный  электронный  документ  с  электронной  цифровой  подписью  .  Абоненту  B  известен  секретный  ключа  ,  открытый  ключ  ,  число    и  составной  модуль  .

Уравнение  проверки  ЭЦП,  по  схеме  1  (см.  таблица  1)  имеет  вид: 

.  (7)

Вычисляются  по  отдельности  левая    и  правая    части  уравнения:

,  (8)

.  (9)

Если  обе  части  уравнения  проверки  равны,  то  электронная  цифровая  подпись  соответствует  документу  и  его  можно  считать  подлинным.  Если  же  результаты  отличаются,  то  подпись  поддельная. 

Для  восстановления  скрываемой  информации  получателю  потребуется  вычислить    из  уравнения  формирования  подписи  1  (таблица  1): 

.  (10)

Абонент  В  вычисляет  ,  а  затем  производит  операцию  дешифрования  скрытого  сообщения  по  заранее  известному  абонентам  А  и  В  алгоритму  и  ключу. 

Недостатком  организации  скрытого  канала  на  основе  выше  предложенных  схем  ЭЦП  является  необходимость  передачи  секретного  ключа    абоненту  В.  Указанный  недостаток  можно  преодолеть,  используя  схемы  формирования  и  проверки  ЭЦП  Эль-Гамаля  с  составным  модулем,  приведенные  в  таблице  2.

Таблица  2.

Варианты  ЭЦП  с  составным  модулем  для  формирования  скрытого  канала  без  знания  секретного  ключа

где:  —  некоторая  трудно  обратимая  сжимающая  функция, 

—  простое  число  длиной  160—256  бит  (),  . 

Для  программной  реализации  скрытого  канала  на  основе  схем  ЭЦП  Эль-Гамаля  с  составным  модулем,  представленных  в  таблице  1  и  2,  выбран  язык  объектно-ориентированного  программирования  Java  и  среда  программирования  NetBeans  IDE  7.0.1.  Язык  Java  обладает  такими  достоинствами  как  многозадачность,  поддержка  протоколов  Internet  и  многоплатформенность  [1]. 

Рассмотрим  результаты  реализации  алгоритма  скрытого  канала  на  основе  первой  схемы  ЭЦП  с  составным  модулем,  из  таблицы  2,  на  языке  программирования  Java  в  среде  NetBeans  IDE  7.0.1:

На  подготовительном  этапе  генерируем  большое  простое  число  ,  ,  :  размером  256  бит:

=223096956678164115651437  3612860150572827242382955591950668225474862  195232833177.

=3212596176165563265380698002518616824871229031456052408962244683801  56113527977489.

=58005208736322670069373713934363914893508301956845390717373862346417  0760536626021.

Составной  модуль  =18634731178399553393445422055225217906696381624222  90872734543483088411386334894729928382552789219962253585121487104549981271287969824464384687298933644

72099641269.

Выбираем  наименьшее  число  ,  такое,  что  :  ,  затем  абонент  А  выбирает  секретный  ключ  ,  любое  число  меньшее  чем  n:

Секретный  ключ  =1865956567500816360436111850039724044944261261672768  531827962123727123172427196.

Конфиденциальную  информацию  небольшого  размера  шифруют  с  помощью  заранее  согласованного  между  абонентами  А  и  В  криптоалгоритма  и  используют  полученное  число  в  качестве  параметра  ,  который  используется  как  скрытый  канал  для  передачи  секретного  сообщения  M  =  11255224242534323511332424511334234111424344  43.

Затем  вычисляем  открытый  ключ    по  формуле  :

=71840930417089354757374236708262931343664636159708279936556274182422444328592894087752257384584357119

55560432519274767342950647891586737806112321301397625873297.

Вычисляем  параметр  ЭЦП    по  формуле  :

=16251723041192144579785344064610502292172824907074943398922427662065422989109500447296214677802

603917311878873752330003012408058666786745680257262020603994134196.

Затем  по  формуле    непосредственно  вычисляем  параметр  ,  электронной  цифровой  подписью  данного  документа  будет  пара  чисел  :

=217978963086132416663196552107546965867339260503691558062969389885  0338444090429.

Для  проверки  ЭЦП  программное  обеспечение  вычисляет  по  отдельности  левую  и  правую  части  следующего  уравнения  . 

Левая  часть  уравнения  проверки  =1494167031522822443987997739723015600399786629558425882381457506787747233017655212875882095932620252051340603

29145350887334768927007186534837339764185835564825794.

Правая  часть  уравнения  проверки  =1494167031522822443987997739723015600399786629558425882381457506787747233017655212875882095932620252051340603

29145350887334768927007186534837339764185835564825794.

Обе  части  уравнения  проверки  равны,  следовательно,  электронная  цифровая  подпись  соответствует  электронному  документу  и  его  можно  считать  подлинным.

В  качестве  мер  защиты  от  организации  скрытого  канала  передачи  данных  предлагаются  схемы  с  упрощенным  уравнением  проверки  подписи,  представленные  в  таблице  3  [2].  Основываясь  на  сложности  извлечения  корней  по  составному  модулю,  в  данных  схемах  электронной  цифровой  подписью  является  число  ,  которое  вычисляется  по  формуле:

.  (11)

Для  вычисления  по  известным    и  n  необходимо  решить  задачу  дискретного  логарифмирования,  эффективного  алгоритма  решения  которой  на  данный  момент  времени  не  существует.

Таблица  3.

Схемы  с  упрощенным  уравнением  проверки  подписи

Выводы.  В  схемах  ЭЦП,  представленных  в  таблице  1,  возможна  организация  скрытого  канала  передачи  данных,  но  для  этого  необходимо  передать  абоненту  В  секретный  ключ  .  В  то  время  как,  в  схемах,  представленных  в  таблице  2,  организация  скрытого  канала  передачи  данных  возможна  без  передачи  секретного  ключа  .

В  качестве  защиты  от  организации  скрытого  канала  передачи  данных  авторы  предлагают  использовать  схемы  с  упрощенным  уравнением  проверки  подписи,  представленные  в  таблице  3,  в  которых  не  возможна  реализация  скрытого  канала,  т.к.  нахождение  параметра  из  уравнения  проверки  подписи  является  задачей  нахождения  дискретного  логарифма  не  решенной  в  общем  случае  к  настоящему  времени.

Список  литературы:

1.Джон  Родли.  Создание  Java-апплетов.  —  The  Coriolis  Group,  Inc.,  1996,  Издательство  ИПФ  «ДиаСофт  Лтд.»,  1996.

2.Молдовян  Н.А.  Криптография  с  открытым  ключом.  /  Н.А.  Молдовян,  А.А.  Молдовян,  М.А.  Еремеев.  —  СПб.:  БХВ  —  Петербург,  2004.  —  288  с.

3.Ниссенбаум  О.В.  Криптографические  протоколы:  Учебное  пособие.  Тюмень,  2007.  —  139  с.

4.Шнайер  Б.  Прикладная  криптография.  Протоколы,  алгоритмы,  исходные  тексты  на  языке  Си.  /  Б.  Шнайер  —  М.:  Издательство  ТРИУМФ,  2003.  —  816  с.

5.Simmons  G.J.  The  Prisoner`s  Problem  and  the  Subliminal  Channel  //  Advances  in  Cryptography:  Proceeding  of  EUROCTYPT  `83,  Plenum  Press,  1984.  P.  51—67.