ПОИСК  РЕШЕНИЯ  ДЛЯ  ЧАСТНОГО  СЛУЧАЯ  ОДНОЙ  NP-ТРУДНОЙ  ЗАДАЧИ  ТЕОРИИ  РАСПИСАНИЙ

Шпеник  Татьяна  Борисовна

старший  преподаватель  кафедры  компьютерных  систем  и  сетей  Ужгородскоого  Национального  университета,  г.  Ужгород

E-mail: 

Предлагается  алгоритм  поиска  оптимального  решения  для  задачи  теории  расписаний,  которая  принадлежит  классу  -трудных  [1,  с.  252].  К  данному  классу  относится  большинство  задач  теории  расписаний  и  реализация  поиска  их  оптимального  решения  требует  больших  временных  затрат.  Поэтому  исследование  свойств  оптимальных  расписаний  и  построение  на  их  основе  эффективных  приближенных  алгоритмов  [2,  c.  52],  а  также  точных  алгоритмов  решения  частных  случаев  задач  [3,  c.  157],  [4,  c.  118]  являются  актуальными  проблемами  в  теории  расписаний.  Причем,  как  показывает  практика,  многие  -трудные  задачи  остаются  трудными  и  с  точки  зрения  нахождения  нетривиальных  приближенных  решений.  Обзор  публикаций  показывает,  что  интерес  представляет  случай,  когда  работы  обслуживаются  приборами  разной  производительности.

В  данной  работе  рассматривается  следующая  задача.  В  обслуживающую  систему  параллельных  приборов    одновременно  (в  момент  времени  )  поступает  конечное  множество    независимых  работ,  каждая  из  которых    должна  быть  выполнена  не  позднее  установленного,  общего  для  всех  работ,  директивного  срока  .  Задано  время  ,  необходимое  для  выполнения  работы    прибором  с  производительностью  ,  а  также  производительность    каждого  из  приборов  .  Время  ,  необходимое  для  выполнения  работы    прибором  j,  вычисляется  по  формуле

Величину    назовем  длительностью  работы  i  ().  Очевидно,  что  каждый  из  приборов  j  (),  за  время    может  выполнить  работы  суммарной  длительностью  .  Прерывания  процесса  выполнения  работ  запрещены.

Рассматриваемая  обслуживающая  система  является  одностадийной,  а  именно:

·     каждый  прибор    может  выполнять  любую  работу  ;

·     в  произвольный  момент  времени    каждая  работа    выполняется  не  более,  чем  одним  прибором,  и  каждый  прибор    выполняет  не  больше  одной  работы.

Приборы  не  выходят  из  строя,  и  переход  от  выполнения  одной  работы  к  другой  осуществляется  моментально,  без  затрат  времени.  Необходимо  найти  минимальное  число    обслуживающих  приборов,  которые  обеспечат  завершение  выполнения  всех  работ  до  заданного  момента  времени  .  Данная  задача,  являясь  NP-трудной  в  случае,  когда  прерывания  процесса  выполнения  работ  запрещены,  становится  тривиальной,  когда  прерывания  разрешены.  В  этом  случае

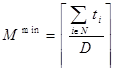
где:    —  наименьшее  целое  число  такое,  что  .

Далее  будем  считать,  что  работы  перенумерованы  в  порядке  не  возрастания  их  длительностей,  а  именно

,  ,

а  приборы  —  в  порядке  не  возрастания  их  производительностей,  то  есть

,  .

Теорема.  Существует  оптимальное  (по  количеству  приборов)  расписание  выполнения  работ,  в  котором  для  произвольного  прибора    справедлива  система  неравенств

,  ,  .  (1)

Здесь    —  количество  приборов,  которые  заняты  выполнением  работ,    —  момент  завершения  выполнения  работ  прибором  ,    —  время  выполнения  работы,  которая  выполняется  прибором    -й  по  порядку,    —  количество  работ,  которое  выполняется  прибором  .

Доказательство.  Рассмотрим  оптимальное  расписание  .  Допустим,  что  для  некоторого  прибора    условие  (1)  не  выполняется.  Тогда  существуют  такие    и  ,  что  ,  то  есть  некоторая  работа  ,  которая  в  расписании    выполняется  прибором  ,  может  быть  выполнена  прибором    вместе  с  другими  работами.  Таким  образом,  можно  построить  новое  расписание  выполнения  работ  ,  в  котором  работу    назначено  на  выполнение  прибором  ,  а  для  всех  других  работ  распределение  по  приборам  сохранено  таким  же,  как  и  в  расписании  .  Очевидно,  что  количество  приборов,  занятых  выполнением  работ  в  расписании    не  увеличилось  и  расписание  допустимое,  а  по  этому  и  оптимальное.  Если  для  расписания    условие  (1)  выполняется,  то  теорема  доказана,  иначе  к  расписанию    используем  аналогичные  рассуждения  и  построим  следующее  оптимальное  расписание.  Учитывая,  что  количество  работ  и  приборов  конечны,  и  при  переходе  от  расписания  S  к  расписанию    для  одной  из  работ  номер  прибора,  который  ее  обслуживает,  уменьшается,  то  за  конечное  количество  шагов  можно  построить  оптимальное  расписание,  для  которого  условие  (1)  выполняется.  Теорема  доказана.

Из  доказанной  теоремы  следует,  что  при  решении  задачи  можно  ограничиться  рассмотрением  расписаний,  для  которых  имеют  место  неравенства  (1).  Каждому  такому  расписанию  поставим  в  соответствие  перестановку  ,  где  —  количество  приборов,  которые  заняты  выполнением  работ,    —  количество  работ,  а    —  последовательность  номеров  работ,  которые  выполнены  прибором  .

Теоретически  оптимальным  будем  считать  расписание,  которому  соответствует  число  приборов

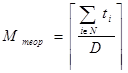,  (2)

(данную  величину  будем  рассматривать  как  нижнюю  оценку  количества  приборов  в  оптимальном  расписании). 

Разработанный  алгоритм  состоит  в  построении  начального  допустимого  расписания  на  нулевом  этапе,  и  последовательном  улучшении  расписания  на  последующих  этапах. 

Алгоритм.

0-й  этап.  k-й  шаг  .  На  k-м  шаге  строится  расписание  выполнения  работ  k-м  прибором.  Пусть  для  k-го  прибора  определены  первые  r  работ  (исходное  r=0).  Обозначим  через    множество  невыполненных  работ  ,  для  которых    (на  нулевом  этапе  ).  Для  каждого    вычислим  .  Через    обозначим  момент  времени  завершения  выполнения  первых  r  работ  k-м  прибором  (). 

Если  выполнение  k-м  прибором  любой  из  невыполненных  работ    (на  нулевом  этапе)  невозможно,  то  есть  условие

  (3)

не  выполняется,  будем  считать,  что  k-й  прибор  загружен  числом  работ,  которое  равно  ,  а  номера  работ,  которые  выполнены  данным  прибором,  образуют  перестановку  .

Если  условие  (3)  выполняется  для  некоторых  ,  то  среди  таких  работ  выбирается  работа  с  наименьшим  номером  и  включается  в  расписание  выполнения  работ  k-м  прибором,  а  r,  соответственно,  увеличивается  на  единицу.  Процесс  повторяется  до  тех  пор,  пока  прибор  с  номером  k  не  будет  загружен  или  пока  не  будут  выполнены  все  работы.

Как  только  k-й  прибор  загружен,  определяется

  (4)

и  выполняется  переход  на  -й  шаг.  При  этом  для  каждого    вычисляется  ,  то  есть  последовательность  величин  ,  где  і  принадлежит  множеству  невыполненных  работ  ,  восстанавливается.

Когда  все  работы  выполнены,  мы  получим  некоторое  допустимое  расписание,  в  котором  работы  выполняются  на    приборах  и  перестановку  .  В  случае,  когда    мы,  очевидно,  получим  оптимальное  решение  и  искомую  величину  М^min  (она  равняется  ).

В  случае,  когда  ,  переходим  к  следующему  этапу  алгоритма,  пытаясь  построить  расписание  выполнения  работ  на    приборах,  где  _.

j-й  етап  .  На  j-м  этапе  выполняется  построение  допустимого  решения  задачи  для    приборов,  где

.  (5)

Выбор    из  формулы  (5)  реализует  поиск  оптимального  расписания  методом  дихотомии.  На  первом  шаге  в  качестве    выбирается  ,  которое  вычислено  согласно  (2),  а  в  качестве    выбирается  .

Из  построения  расписания  на  -м  приборе,  очевидно,  следует,  что  в  случае,  когда  расписание  выполнения  работ  на    приборах  существует,  то  соответствующая  ему  перестановка    будет  лексикографически  больше  перестановки  .  По  этому  работы  включаются  в  порядке  их  следования  в  .

Пусть

 ,

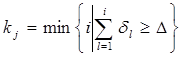Где

,  .

Величину    будем  называть  максимально  допустимым  простоем  для  приборов.  Работы,  которые  выполнялись  прибором  i,  где  ,  считаются  невыполненными.  Поставим    и  перейдем  на  k-й  шаг.

k-й  шаг.  Будем  считать,  что  расписание  выполнения  работ  приборами    является  фиксированным  из  предыдущего  расписания.  Для  каждого    вычислим  .  Условие  (3)  остается  условием  загруженности  k-го  прибора.  Схема,  согласно  которой  он  загружается,  та  же,  что  и  на  нулевом  этапе.

Как  только  k-й  прибор  загружен,  из  (4)  определяется    и  выполняется  проверка  следующего  условия:

.  (6)

Если  условие  (6)  удовлетворяется,  то  возможны  случаи:

1.  все  работы  выполнены.  В  этом  случае  расписание  выполнения  работ  на    приборах  построено  и  переходим  к  -му  этапу,  приняв  ,  а  последовательность  величин  ,  ,  приводим  к  ее  первоначальному  виду.

2.  работы  выполнены  не  все.  Тогда  последовательность  величин  ,  где  і  принадлежит  множеству  невыполненных  работ  ,  восстанавливаем  и  переходим  на  -й  шаг  j-го  этапа.

Если  условие  (6)  не  удовлетворяется,  то  из  последовательности  работ,  которые  выполняются  на  k-м  приборе,  исключается  последняя.  Пусть  это  работа  с  номером  p.  Если  условия

   (7)

И

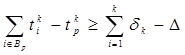   (8)

выполняются  (если  условие  (8)  нарушается,  то  даже  при  выполнении  всех  работ    на  k-м  приборе  условие  (6)  не  выполняется),  то  начиная  с  работы  ,  загрузка  k-го  прибора  работами  осуществляется  согласно  предыдущей  схеме.  Таким  образом,  если  после  загрузки  k-го  прибора  и  перерасчета    по  формуле  (4)  условие  (6)  выполняется,  то  выполняется  переход  на  -й  шаг. 

Если  хотя  бы  одно  из  условий  (6)—(8)  не  выполняется  и  ,  то  выполняется  переход  на  -й  шаг  (при  этом  последняя  в  списке  выполненных  этим  прибором  работ  исключается  из  расписания  и  в  качестве  p  используется  при  его  загрузке).  Если  же  ,  то  расписания  выполнения  работ  на    приборах  не  существует.

В  случае,  когда  с  учетом  (6),  для  выбранного  значения    расписания  построить  не  удалось,  уточняется    и  выполнение  алгоритма  продолжается,  начиная  с  -го  этапа,  где  последовательности  величин  ,    придается  исходный  вид  и  строится  расписание  выполнения  работ  на    приборах. 

Процесс  повторяется  до  тех  пор,  пока  .

Конец  алгоритма.

В  результате  выполнения  алгоритма  будет  построена  лексикографически  возрастающая  по    последовательность  расписаний.  Оптимальным,  по  количеству  приборов,  расписание  будет  последнее  построенное  допустимое  расписание,  где  выполнение  работ  осуществляется  на    приборах. 

Список  литературы:

1.Лазарев  А.А.,  Гафаров  Е.Р.  Теория  расписаний.  Задачи  и  алгоритмы.  —  М.:МГУ,  2011.  —  222  с.

2.Кузюрин  Н.Н.,  Фомин  С.А.  Эффективные  алгоритмы  и  сложность  вычислений.  —  М.:МФТИ,  2007.  —  326  с.

3.j25eph  Y.-T.  Leung  (Ed.)  Handbook  of  Scheduling.  Algorithms,  Models,  and  Performance  Analysis.  Boca  Raton,  FL,  USA:  Chapman  &  Hall  /  CRC,  2004.  —  1216  c.

4.Кузка  А.И.,  Шпеник  Т.Б.  Алгоритм  последовательного  анализа  вариантов  для  минимизации  числа  приборов  в  задаче  составления  расписания,  удовлетворяющего  директивным  срокам  //  Кибернетика  и  системный  анализ.  —  2000.  —  №  5.  —  С.  118—123.