ФИЗИКО-МЕХАНИЧЕСКАЯ  МОДЕЛЬ  ОДНООСНООРИЕНТИРОВАННОГО ПОЛИМЕРНОГО  МАТЕРИАЛА

Рымкевич  Павел  Павлович

канд.  физ.-мат.  наук,  проф.  СПбГУСЭ,  г.  Санкт-Петербург

Головина  Виктория  Владимировна

преподаватель  ВКА  им.  А.Ф.  Можайского,  г.  Санкт-Петербург

Романова  Алла  Александровна

канд.  тех.  наук,  доц.  СПбГУСЭ,  г.  Санкт-Петербург

Коцкович  Владимир  Богданович

канд.  тех.  наук,  доц.  СПбГУСЭ,  г.  Санкт-Петербург

E-mail:  romallaa@yandex.ru

Современные  полимерные  материалы  используются  практически  во  всех  областях  техники.  Для  описания  вязкоупругого  поведения  одноосноориентированных  полимерных  материалов,  например,  нитей,  стержней,  разработан  ряд  теорий  нелинейной  вязкоуп­ругости  [1,  8,  11,  14],  основанных  на  известном  принципе  Больцмана.  Большинство  этих  теорий  отличается  видом  ядра  релаксации  и  осно­вывается  либо  на  анализе  экспериментальных  данных,  либо  на  общих  физических  аналогиях  [2,  с.  4—7,  12].  Как  показано  в  классических  работах,  описывающих  поведение  полимерных  материалов  при  воздей­ствии  температурного  фактора  и  механических  нагрузок  [2,  6,  11],  основным  фактором,  определяющим  вязкоупругое  поведение  данного  типа  материалов,  является  преодоление  различных  по  высоте  и  ширине  потенциальных  барьеров.  Обобщая  результаты  работ  [3,  4,  7,  12,  13,  15],  можно  сделать  предположение  о  том,  что  при  получении  полимерных  нитей  и  пленок  в  результате  одноосной  ориентационной  вытяжки  при  высоких  температурах  материал  переходит  в  метастабильное  состояние,  при  котором  обратные  переходы  «заморожены».  Впервые  идея  о  квантованности  деформации  в  синтетических  нитях  изложена  в  работе  [9]  и  развита  в  работе  [10].

При  изучении  поведения  полимерных  материалов  следует  рассматривать  три  уровня  иерархии  структур:  молекулярный  уровень,  уровень  мезаструктуры  (так  называемый  надмолекулярный  уровень)  и  макроуровень  (поведение  материала  как  целого  объекта).  Молеку­лярный  уровень  характеризуется  временами  релаксации  10⁻¹²  —  10⁻⁶  с  и  не  может  отвечать  за  «долговременные»  процессы  ползучести  и  релаксации  напряжения.  Молекулярный  уровень  определяет  упругие  свойства  материала  с  соответствующими  временами  релаксации.  Весьма  сложная  и  многообразная  надмолекулярная  структура  ориентиро­ванных  аморфно-кристаллических  полимеров  определяет  мезоуровень.  При  деформировании  материалов  данного  класса  основную  долю  деформации  составляет  обратимая  вязкоупругая  часть  деформации.  В  общем  случае  полную  деформацию    можно  представить  в  виде  суммы  упругой  (),  вязкоупругой  или  конформационной  ()  и  необратимой  ()  частей  деформации,  а  именно:

.                                                                           (1)

Скачкообразность  и  длительность  процессов  деформирования  свидетельствует  о  том,  что  все  основные  перестройки  при  деформи­ровании  полимеров  происходят  на  мезоуровне  с  достаточно  большими  временами  релаксации  (10⁻³  —  10²  с).  Таким  образом,  следует  признать,  что  на  мезоуровне  полимеры  в  нагруженном  состоянии  могут  находиться  в  различных  квазиравновесных  состояниях.  Наиболее  правдоподобной  является  гипотеза  о  том,  что  на  мезоуровне  отдельные  устойчивые  структуры  (кластеры)  могут  находиться  в  двух  устойчивых  состояниях.  Разделенных  энергетическим  барьером  высотой    и  шириной  .  В  соответствии  с  терминологией,  принятой  в  работе  [14],  данные  устойчивые  структуры  будем  называть  активными  конформационными  элементами  (в  дальнейшем  АКЭ),  природа  которых  для  механического  описания  не  имеет  принци­пиального  значения.  Переход  из  одного  устойчивого  состояния  в  другое  сопровождается  квантом  деформации  .  При  таком  подходе  вязкоупругая  часть  деформации  лимитируется  обратимыми  переходами  АКЭ  из  одного  состояния  в  другое.  Одно  из  устойчивых  состояний  АКЭ  с  минимальным  линейным  размером  —  состояние  1  —  будем  называть  условно  свернутым  и  обозначать  .  Второе  устойчивое  состояние  2  будем  называть  условно  развернутым  и  обозначать  .  В  ненагруженном  состоянии  кластер  находится  либо  в  состоянии  1,  либо  в  состоянии  2,  разделенным  энергетической  щелью  шириной  .  В  большинстве  случаев  состояние  1  более  устойчивое  (),  хотя  модель  не  исключает  и  состояния  с  .

Высоты  барьеров    и  энергетические  зазоры    будем  называть  высокими,  если    или    значительно  больше  ,  и  низкими  в  противном  случае.  Как  принято  в  молекулярной  физике  высоту  барьера  будем  измерять  в  Кельвинах.  Переход  к  обычным  физическим  единицам  осуществляется  через  известные  постоянные    и  .  На  макроскопическом  уровне  между  элементами  мезаструктуры  происходит  обмен  энергией  и  импульсом,  что  приводит  к  общему  уменьшению  свободной  энергии  всей  системы,  т.  е.  происходит  вырав­нивание  макроскопических  флуктуаций,  возникающих  на  мезоуровне.  Макроскопически  в  процессе  релаксации  данный  механизм  прояв­ляется  в  перераспределении  нагрузки  между  разными  молекулярными  структурами. 

Необратимую  часть  деформации  будем  рассматривать  как  прин­ципиально  обратимую  при  высоких  температурах,  полученную  при  термическом  ориентировании  и  после  охлаждения  разделенную  высоким  энергетическим  барьером.  В  данной  части  работы  будет  рассмотрена  только  обратимая  часть  деформации,  т.  е.  принимается  в  соотношении  (1)  .

Таким  образом,  обобщенную  физическую  модель  ориентиро­ванного  полимерного  материала  можно  представить  в  виде  набора  кластеров  (АКЭ)  с  набором  следующих  характеристик:  ,  ,  ,  ,  .

Здесь,    —  номер  типа  кластера;    —  высота  барьера;    —  ширина  энергетического  зазора;    —  величина  кванта  деформации;    и    —  числа  заполнения  состояний.  В  ненагруженном  состоянии  числа  заполнения    и    определяются  в  соответствии  со  статистикой  Больцмана,  за  исключением  «высоких»  барьеров,  где  числа  заполнения    и    определяются  технологией  создания  образцов,  при  этом  уровни  с  числом  заполнения    чаще  всего  перенаселены.  При  термической  усадке  числа  заполнения    и    принимают  равновесные  значения.

При  выводе  основного  локального  определяющего  уравнения  сделаем  ряд  упрощающих  допущений.

Д1.  На  мезоуровне  кластеры  системы  могут  находиться  в  двух  энергетических  состояниях:  условно  свернутом  состоянии  1,  энергию  которого  в  ненапряженном  состоянии  примем  равной  нулю.  И  в  ориентированном  состоянии  2,  энергию  которого  примем  равной  ,  разделенных  барьером  высотой  .  При  переходе  АКЭ  из  состояния  1  в  состояние  2  высвобождается  (рождается)  квант  деформации    и  поглощается  при  противоположном  переходе.  Так  как  внешняя  сила  оказывает  активирующее  действие  на  АКЭ,  понижая  потенциальный  барьер  на  величину  упругой  энергии,  являющейся  квадратичной  функцией  от  величины  деформации,  в  направлении  прямого  перехода  и  наоборот,  повышая  величину  барьера  (эту  работу  надо  дополнительно  совершить  против  внешних  сил)  в  противоположном  направлении.  Значение  энергии    можно  рассматривать  как  некоторое  нестабильное  промежуточное  короткоживущее  состояние,  аналогом  которого  является  активиро­ванный  комплекс  в  химии  или  компаунд-ядро  в  ядерной  физике.

Д2.  Примем,  что  числа  заполнения  состояний  1  и  2  подчиняются  в  равновесном  состоянии  статистике  Больцмана.  Обозначим  через    и    числа  заполнения  АКЭ  на  единицу  длины  образца,  причем  согласно  статистике  Больцмана

(2)

,

где:    —  полное  число  АКЭ  на  единицу  длины  образца.

Таким  образом,  числа  заполнения    и    не  зависят  от  высоты  барьера,  а  определяются  шириной  энергетического  зазора  .  Высота  барьера  определяет  кинетику  процесса  деформирования.

Д3.  Упругая  часть  деформации  подчиняется  закону  Гука,  то  есть:

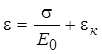.                                                                                     (3)

Д4.  Обратимые  переходы    статистически  независимы  (модель  радиоактивного  распада).  Таким  образом,  в  данной  модели  рассматриваются  лишь  спонтанные  переходы.  Однако,  как  показывают  результаты  анализа,  имеет  смысл  рассмотреть  модели,  содержащие  и  вынужденные  переходы,  то  есть  ввести  взаимодействие  АКЭ  между  собой.  Для  рождения  и  уничтожения  квантов  деформации  можно  использовать  методы  вторичного  квантования.  Следовательно,  данная  модель  эквивалентна  модели  идеального  газа  из  активных  конфор­мационных  элементов.

Д5.  Высота  энергетического  барьера    определяется  хими­ческим  строением  полимера.  Примем,  что  при  данной  температуре  в  размороженном  состоянии  находится  лишь  один  тип  обратимых  переходов.

При  выводе  локального  определяющего  уравнения  рассмотрим  «физически  бесконечно  малый  объем»  полимера,  содержащий  достаточно  большое  число  АКЭ.  Пусть    —  локальная  плотность  АКЭ  —  в  общем  случае  случайная  локальная  величина.  Причем    из  них  находится  в  состоянии  1  и    —  в  состоянии  2,  соответственно,  в  момент  времени  .  Пусть  в  стационарном  недеформированном  состоянии  эти  числа  равны    и    соответственно.  Тогда  локальное  определяющее  уравнение  можно  представить  в  виде:

.                                                                              (4)

В  дальнейшем  упругую  часть  деформации  для  простоты  будем  обозначать  через  ,  то  есть  .  В  общем  случае  стационарное  состояние  является  по  определению  устойчивым,  но  не  обязательно  состоянием  термодинамического  равновесия.

Пусть    и    –  вероятности  перехода  в  единицу  времени  из  состояния    в  состояние    и  наоборот.  При  этом  по  Больцману

                                                                                            (5)

,

где:    и    —  вероятности  перехода  в  единицу  времени  из  состояния    в  состояние    и  наоборот,  которые  определяются  приведенной  высотой  потенциального  барьера,

  —  частота  подхода  к  барьеру.

                                                                                            (6)

,

здесь    —  структурно-чувствительный  коэффициент,  который  определяется  упругой  энергией  АКЭ.

В  стационарном  состоянии

                                                                                            (7)

,

Если  в  начальный  момент  времени  система  находится  в  равновесном  ненапряженном  состоянии,  то

                                          (8)

здесь    и    —  вероятности  перехода  в  единицу  времени  из  состояния  1  в  состояние  2  и  наоборот  без  нагрузки.  Из  соотношения  (8)  следует  распределение  Больцмана,  то  есть  соотношение  (2).

Для    можно  написать  очевидное  кинетическое  уравнение

.                                                           (9)

С  учетом  уравнения  (4)  будем  иметь

Или

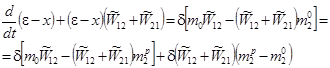                                      (10)

С  учетом  (7)  будем  иметь:

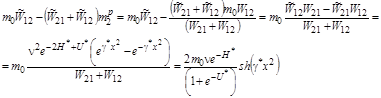                              (11)

Введем  дополнительные  обозначения:

  —  внутреннее  время  релаксации,  определяемое  высотой  барьера;

;    —  константа  материала,  слабо  зависящая  от  температуры;

  —  безразмерное  время;

  —  начальная  деформация  в  отсутствии  упругих  напряжений. 

С  учетом  соотношений  (10)  и  (11)  окончательный  вид  локального  определяющего  уравнения  вязкоупругости  примет  вид:

                                .(12)

В  большинстве  случаев  начальное  состояние,  от  которого  отсчитывается  деформация,  можно  считать  равновесным,  и  в  этом  случае  .  При  наличии  нескольких  типов  АКЭ  можно  ввести  часть  конформационной  деформации,  вызываемой  только  опреде­ленным  типом  АКЭ,  то  есть

.                                                            (13)

Общую  деформацию,  включая  и  возможную  необратимую  часть,  можно  представить  в  виде:

.                                                                 (14)

Для  каждого  типа  кластеров  можно  написать  определяющее  уравнение  в  виде:

.                                                      (15)

Система  уравнений  (14)  и  (15)  дает  полное  детальное  описание  вязкоупругости  ориентированных  полимерных  материалов.  Однако,  для  описания  большинства  явлений  вязкоупругости  достаточно  уравнения  (12).

Использование  уравнения  (12)  в  качестве  определяющего  уравнения  вязкоупругости  показывает,  что  модель  с  одним  типом  АКЭ  вполне  адекватно  описывает  наблюдаемые  экспериментальные  данные.  Однако,  результаты  по  ползучести  для  «больших»  времен  выдер­живания  под  нагрузкой  имеют  ряд  особенностей.  Во-первых,  они  хорошо  укладываются  в  экспоненциальную  зависимость,  но  со  значительно  большим  временем  релаксации,  то  есть  для  описа­ния  длительной  ползучести  необходимо  добавить  еще  одно  слагаемое,  не  вытекающее  из  уравнения  (12).  Во-вторых,  данные  по  длительной  ползучести  (  мин)  весьма  сильно  разбросаны  для  разных  образцов  с  одной  и  той  же  степенью  вытяжки.

Отметим,  что  уравнение  (12)  является  локальным,  и  линейная  плотность  АКЭ  является  случайной  величиной.  Поэтому  опреде­ляющее  уравнение  для  всего  образца  должно  содержать  поправочные  слагаемые.  С  позиций  физики  полное  описание  макроскопической  системы  должно  подчиняться  принципу  иерархии  времён  релаксации.  Согласно  этому  принципу  равновесие  сначала  наступает  на  локальном  уровне  с  соответствующим  временем  релаксации  ,  то  есть  локальная  свободная  энергия  имеет  локальный  минимум,  при  этом  суммарная  свободная  энергия  не  достигает  наименьшего  значения.  Таким  образом,  механическое  напряжение  не  одинаково  по  всему  образцу.  В  механике  твердого  тела  этот  факт  широко  известен.  Выравнивание  свободной  энергии  (стремление  свободной  энергии  к  глобальному  минимуму)  характеризуется  временем  релаксации  системы  .  Этот  факт  можно  учесть,  используя  теорию  возмущений.

Пусть    —  нормированная  функция  распределения  АКЭ  по  объему,  зависящая  от  методики  приготовления  образцов.  Обозначим  через

,

                                                                                          (16)

,

соответственно,  среднее  значение  и  дисперсия  случайной  величины  .

При  заданном  режиме  деформирования    механическое  напряжение    ()  есть  решение  локального  уравнения,  которое  является  функцией  параметра  ,  то  есть  определяется  числом  «работающих»  АКЭ.  Обозначим  через  m

.                                         (17)

Таким  образом,    является  механическим  напряжением,  приложенным  ко  всему  образцу,  то  есть  величина,  непосредственно  определяемая  из  эксперимента  (наблюдаемая  физическая  величина).  Считая,  что  разброс  по    не  является  значительным  (нет  макро­скопических  дефектов  структуры), 

.                                           (18)

  —  является  малой  поправкой  в  локальном  уравнении  (12).  При  этом 

.                                        (19)

Произведем  линеаризацию  уравнения  (12)  с  учетом  (18),  сохраняя  только  слагаемые  первой  степени  по  .  В  результате  имеем:

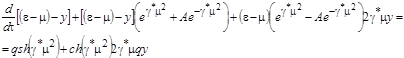(20)

Умножим  левую  и  правую  части  уравнения  (20)  на    и  проинтегрируем  по  всем  значениям    с  учетом  (19),  получим  следующее  выражение:

,    (21)

где  поправка    определяется  из  условия

.                                               (22)

Для  получения  замкнутой  системы  уравнений  умножим  выражение  (20)  на    и  произведем  интегрирование  по  всем  возможным  значениям  :

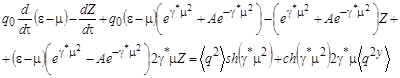                       (23)

Учтем,  что

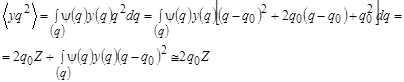                           (24)

Здесь  второе  слагаемое  содержит  компонент  более  высокого  порядка  малости  по  степени  .  С  учетом  соотношений  (16)  и  (21)  получим:

,                                                         (25)

где: 

.                      (26)

Таким  образом,  описание  одноосноориентированного  полимер­ного  материала  с  учетом  неоднородностей  сводится  к  решению  системы  двух  обыкновенных  дифференциальных  уравнений,  связы­вающих  между  собой  деформацию    (режим  деформирования),    —  усредненное  механическое  напряжение  внутри  образца  и  усредненную  поправку  к  механическому  напряжению  .  Окончательно,  данную  систему  уравнений  можно  представить  в  виде:

                                        (27)

.            

Система  уравнений  (27)  дает  полное  описание  процессов  вязкоупругости  в  изучаемых  одноосноориентированных  полимерных  материалах.  Решение  задачи  Коши  для  системы  (27)  требует  задания  начальных  условий,  а  также  вида  режима  деформирования. 

В  качестве  реологической  модели  поведения  полимерного  материала  вместо  классических  демпферов  и  гуковских  пружин  (обобщенные  модели  Максвелла  и  Кельвина-Фойгта)  предлагается  модель  последовательно  соединенных  упругих  пружин  АКЭ  с  двумя  устойчивыми  состояниями,  подчиняющихся  законам  статистической  механики.

Список  литературы:

1.Алфрей  Т.  Механические  свойства  высокополимеров.  —  М.:  ИЛ,  1952.  —  720  с.

2.Бугаков  И.  И.  Ползучесть  полимерных  материалов.  —  М.:  Наука,  1973.  —  288  с.

3.Гроссберг  А.Ю.,  Хохлов  А.Р.  Статистическая  физика  макромолекул.  —  М.:  Наука,  1989.  —  344  с.

4.Демидов  А.В.,  Макаров  А.Г.,  Сталевич  А.М.  Вариант  моделирования  нелинейно-наследственной  вязкоупругости  полимерных  материалов  //  Известия  РАН.  Механика  твердого  тела.  —  2009.  —  №  1.  —  С.  155—165.

5.Екельчик  В.С.,  Рябов  В.М.  Об  использовании  одного  класса  наследст­венных  ядер  в  линейных  уравнениях  вязкоупругости  //  Механика  композитных  материалов.  1981.  №  3.  —  С.  393—404.

6.Макаров  А.Г.,  Демидов  А.В.  Методы  математического  моделирования  механических  свойств  полимеров.  —  СПб.:  Изд-во  СПГУТД,  2009.  —  392  с.

7.Макаров  А.Г.,  Демидов  А.В.  Оптимизация  методов  спектрального  моделирования  деформационных  процессов  полимеров.  —  СПб.:  Изд-во  СПГУТД,  2008.  —  280  с.

8.Работнов  Ю.  Н.  Элементы  наследственной  механики  твердых  тел.  —  М.:  Наука,  1977.  —  384  с.

9.Рымкевич  П.П.,  Сталевич  А.М.  Кинетическая  теория  конформационных  переходов  в  полимерах  //  Физико-химия  полимеров:  сб.  науч.  тр.  Тверской  гос.  ун-т.  Вып.  5.  —  Тверь,  1999.  —  С.  52—58.

10.Рымкевич  П.П.,  Романова  А.А.,  Горшков  А.С.,  Макаров  А.Г.  Физические  основы  вязкоупругого  поведения  ориентированных  аморфно-кристал­лических  полимеров  //  Известия  вузов.  Технология  легкой  промыш­ленности.  —  2012.  —  №  2.  —  С.  70—73.

11.Сталевич  А.  М.  Деформирование  ориентированных  полимеров.  —  СПб.:  Изд-во  СПГУТД,  2002.  —  250  с.

12.Сталевич  А.М.,  Макаров  А.Г.  Простейший  вариант  наследственного  ядра  релаксации  ориентированного  аморфно  кристаллического  полимера  //  Физико-химия  полимеров:  сб.  науч.  тр.  Тверской  гос.  ун-т.  Вып.  5.  —Тверь,  1999.  —  С.  58—64.

13.Сандитов  Д.С.,  Бартенев  Г.М.  Физические  свойства  неупорядоченных  структур.  —  Новосибирск:  Наука,  1982.  —  259  с.

14.Ферри  Дж.  Вязкоупругие  свойства  полимеров.  —  М:  Наука,  1970.—  535  с.

15.Romanova  A.A.,  Rymkevich  P.P.,  Gorshkov  A.S.,  Stalevich  A.M.,  Ginzburg  B.M.  A  New  Phenomenon  —  Amplitude-Modulated  Free  Oscillations  (Beatings)  in  Loated,  Highly  Oriented  Fibers  from  Semi  crystalline  Polymers  //  Journal  of  Macromolecular  Science.  Part  B:  Physics.  —  2007.  —  №  46.  —  P.  467—474.