Статья опубликована в рамках: II Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 04 февраля 2013 г.)
Наука: Информационные технологии
Секция: Системный анализ, управление и обработка информации
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
НЕЙРОСЕТЕВЫЕ МОДЕЛИ СНИЖЕНИЯ КОНЦЕНТРАЦИИ ФЕНОЛЬНЫХ СОЕДИНЕНИЙ В ВОДНЫХ СРЕДАХ
Шейнкман Леонид Элярдович
д-р техн. наук, профессор Тульского государственного университета, г. Тула
E-mail: eliard@yandex.ru
Дергунов Дмитрий Викторович
канд. техн. наук,
инженер Тульского государственного университета,
г. Тула
E-mail: dmitrov83@mail.ru
Проблема управлением очисткой промышленных сточных вод, содержащих трудно окисляемые органические соединения, является одной из острых проблем для большинства производственных комплексов России.
Для принятия эффективных управленческих решений, направленных на снижение антропогенного влияния органических соединений, сбрасываемых в составе промстоков, необходим инструмент прогнозирования уровня загрязнителя в воде после осуществления очистки на этапе сброса. Таким инструментом могут послужить нейросетевые регрессионные модели зависимости концентрации загрязнителя от параметров процесса очистки. Применение нейронных сетей для построения прогнозных моделей продиктовано их свойством, воспроизводить чрезвычайно сложные зависимости нелинейным моделированием [4].
На основе экспериментальных исследований, основанных на усовершенствованных окислительных процессах очистки вод, построена матрица оптимального планирования эксперимента, представленная в табл. 1.
Таблица 1.
Матрица полного факторного эксперимента
|
Опыты |
Планирование |
Переменная состояния |
||||||||
|
z0 |
кодированный масштаб |
натуральный масштаб |
||||||||
|
z1 |
z2 |
z3 |
z4 |
x1 |
x2 |
x3 |
x4 |
y |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
0,05 |
100 |
1 |
1 |
0,036 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
0,1 |
100 |
1 |
1 |
0,071 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
0,05 |
200 |
1 |
1 |
0,035 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
0,1 |
200 |
1 |
1 |
0,068 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
0,05 |
100 |
2 |
1 |
0,033 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
0,1 |
100 |
2 |
1 |
0,064 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
0,05 |
200 |
2 |
1 |
0,031 |
|
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
0,1 |
200 |
2 |
1 |
0,061 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
0,05 |
100 |
1 |
2 |
0,032 |
|
10 |
+1 |
+1 |
-1 |
-1 |
+1 |
0,1 |
100 |
1 |
2 |
0,062 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
0,05 |
200 |
1 |
2 |
0,03 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
0,1 |
200 |
1 |
2 |
0,059 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
0,05 |
100 |
2 |
2 |
0,028 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
0,1 |
100 |
2 |
2 |
0,056 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
0,05 |
200 |
2 |
2 |
0,027 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,1 |
200 |
2 |
2 |
0,053 |
В процессе проведения эксперимента, осуществляемого в соответствии с построенной матрицей оптимального планирования (табл. 1) [2]. Сравнивалось воздействие УФ излучения и окислителей на интенсивность разложения органического загрязнителя (бисфенола-А (ВРА)) в модельном растворе при различных концентрациях ВРА — x1 (50 мкг/л, 100 мкг/л); перекиси водорода H2O2 — x2 (100 мг/л, 200 мг/л) и хлорида железа (III) (1; 2 г/л) — x3. Пробы отбирались через 1 и 2 часа после облучения (время облучения t — x4), и измерялась остаточная концентрация ВРА (переменная состояния — y) [5].
При решении задач прогнозирования роль нейронной сети состоит в предсказании будущей реакции системы по её предшествующему поведению. В данном случае нейронная сеть играет роль универсального аппроксиматора функции от нескольких переменных, реализуя нелинейную функцию
|
|
|
где: x — входной вектор;
y — реализация векторной функции нескольких переменных.
Используя нелинейный аппарат нейросетевого моделирования, в программной среде Statistica v. 6.1 решалась регрессионная задача по определению прогнозного уровня остаточной концентрации фенольного соединения в водной среде под действием физико-химических факторов. Исходя из результатов планирования эксперимента параметрами входного вектора являются: начальная концентрация фенольного соединения (С (ВРА)), концентрация перекиси водорода (С (Н2О2)), концентрация хлорида железа (III) FeCl3, выступающего в качестве активатора (СА) и время воздействия на систему ультрафиолетового излучения (t), выходного — остаточная концентрация загрязнителя (Сost).
Из пяти тысяч построенных нейросетевых регрессионных моделей отобраны два четырехслойных персептрона № 194, 4663 (рис. 1).
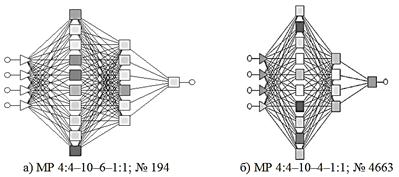
Рисунок 1. Архитектура четырехслойного персептрона
Модели четырехслойного персептрона имеют четырехслойную структуру с четырьмя входными нейронами, одним выходом и двумя скрытыми слоями, содержащими по 10 и 4 нейрона в модели № 4663 и 10 и 6 нейрона в модели № 194.
Результаты работы сетей в задаче регрессии приведены в табл. 2
Таблица 2.
Описательные статистики
|
Статистики |
Номера нейронных сетей |
|
|
194_MP |
4663_MP |
|
|
Среднее данных |
0,046625 |
0,046625 |
|
Ст.откл. данных |
0,015767 |
0,015767 |
|
Среднее ошибки |
0,000216 |
0,000720 |
|
Ст.откл. ошибки |
0,001049 |
0,001070 |
|
Среднее абсолютной ошибки |
0,000728 |
0,000864 |
|
Отношение ст.откл. |
0,066506 |
0,067876 |
|
Корреляция |
0,997856 |
0,997703 |
Наиболее важной статистикой характеризующей качество нейросетевой модели является отношение стандартных отклонений (Отношение ст. откл. или S.D. ratio), представляющее собой отношение стандартного отклонения ошибки прогноза к стандартному отклонению исходных данных. Величина этой статистики составляет 0,066506 для модели MP nn_194 и 0,067876 для MP nn_4663. Величина этой статистики значительно меньшая единицы (Отношение ст. откл. < 0,1 [3]) отражает хорошее качество регрессии, что также подтверждается коэффициентом корреляции Пирсона, между предсказанными и наблюдаемыми выходными значениями, равным для MP nn_194 и nn_4663 соответственно 0,997856 и 0,997703. Долю объясненной дисперсии зависимой переменной в общей выборочной дисперсии по результату работы сети в задаче регрессии характеризует регрессионное отношение. Которое определяется R = 1 — S.D. ratio и равно соответственно 0,933494 и 0,932124 для nn_194 и nn_4663, что составляет 93,35 % и 93,21 %. Высокий процент объясненной дисперсии является универсальной мерой качества нейросетевых регрессионных моделей [3].
Четырехслойные персептроны (рис. 1) обучены на основе алгоритма обратного распространения ошибки и сопряженных градиентов.
Сто эпох (итераций) обратного распространения, двадцать и восемь эпох сопряженными градиентами (ОР100, СГ20, СГ8 b) с ошибкой обучения 0,00482, контрольной ошибкой 0,02105 и тестовой ошибкой 0,05182 сформировали нейронную сеть nn_194. Четырехслойный персептрон nn_4663 сформирован за счет ста итераций обратного распространения, двадцати и пяти итераций сопряженными градиентами (ОР100, СГ20, СГ5 b) с ошибкой обучения 0,006764, контрольной ошибкой 0,033119 и тестовой ошибкой 0,049106.
При обучении сети алгоритмом обратного распространения все наблюдения из обучающего множества на каждой эпохе по очереди подаются на вход сети. Сеть обрабатывает их и выдает выходные значения, которые сравниваются с целевыми выходными значениями, содержащимися в наборе исходных данных. В процессе обучения происходит корректировка весов сети, направленная на уменьшение ошибки, т. е. разности между желаемым и реальным выходом. При обучении вычисляется локальный градиент каждого веса для каждого наблюдения. Веса корректируются после обработки каждого наблюдения по формуле [1, с. 3]:
|
|
|
где: ![]() — скорость обучения;
— скорость обучения;
![]() — локальный градиент ошибки;
— локальный градиент ошибки;
![]() — коэффициент инерции;
— коэффициент инерции;
![]() — выходное значение i-го элемента (пороги считаются весами с
— выходное значение i-го элемента (пороги считаются весами с ![]() );
);
![]() — номер итерации (эпохи).
— номер итерации (эпохи).
В методе спуска по сопряженным градиентам происходит последовательный поиск минимума по различным направлениям на поверхности ошибок. Сначала берется направление наискорейшего спуска, вдоль которого ищется минимум. Направления поиска (сопряженные направления) выбираются из тех соображений, чтобы не терять минимума по тем направлениям, по которым уже произведена минимизация. Градиент ошибки вычисляется как сумма градиентов ошибок по всем обучающим наблюдениям. Начальное направление поиска задается формулой:
|
|
|
где: ![]() — начальное направление спуска;
— начальное направление спуска;
![]() — антиградиент минимизируемой функции в точке x0, т. е.
— антиградиент минимизируемой функции в точке x0, т. е. ![]() .
.
На последующих шагах направление поиска корректируется с помощью формулы Полака-Рибьера:
|
|
|
|
|
|
где: ![]() — направление спуска на j-ом шаге;
— направление спуска на j-ом шаге;
![]() — величина шага;
— величина шага;
![]() — вектор градиента минимизируемой функции на j-ом шаге;
— вектор градиента минимизируемой функции на j-ом шаге;
![]() — транспонированный вектор градиента.
— транспонированный вектор градиента.
В случае если по данному направлению ошибка не убывает, то алгоритм снова берёт направление наискорейшего спуска.
В качестве синаптической в рассматриваемых нейронных сетях используется линейная функция, а в качестве функции активации — линейная на входном и выходном слое и гиперболическая на скрытых слоях.
Уровень активации на вход сети передается в неизменном виде посредством линейной функции активации. Входы на скрытые слои (второй, третий, четвертый) активируются гиперболической функцией, представляющей собой функцию гиперболического тангенса (tanh) [4]:
|
|
|
где: а — коэффициент, характеризующий крутизну функции.
На выходе нейронной сети активация осуществляется линейной функцией, т. е. на выход сети значения с выхода предыдущего слоя передаются в неизменном виде.
Применение нейронных сетей для анализа поведения зависимой переменой, в данном случае концентрации фенольного соединения в сточных водах от параметров процесса очистки — концентрации перекиси водорода, хлорида железа (III), выступающих в качестве окислителя и активатора фотохимической реакции и времени ультрафиолетового воздействия, позволяет выработать механизм управления очисткой промышленных сточных вод, содержащих фенольные соединения.
Список литературы:
1.Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. 2-е изд. (+CD). СПб.: Питер, 2003. 688 с.
2.ГОСТ Р 50.1.040-2002. Статистические методы. Планирование экспериментов. Термины и определения. М. Госстандарт России, 2002. 36 с.
3.Нейронные сети. STATISTICA Neural Networks: Методология и технологии современного анализа данных /Под. ред. В.П. Боровикова 2-е изд., перераб. и доп. М.: Горячая линия — Телеком, 2008. 392 с.
4.Осовский С. Нейронные сети для обработки информации /Пер. с польского И.Д. Рудинского. М.: Финансы и статистика, 2004. 344 с.
5.Чернова М.В. Исследование процесса очистки водных систем от фенольных соединений под действием физико-химических факторов. Дис. канд. техн. наук: 03.00.16. Калуга — Тула, 2009. 118 с.
дипломов


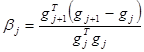 ,
,
Оставить комментарий