МОДЕЛИРОВАНИЕ ПРИЗМАТИЧЕСКОГО ТРЕХФАЗНОГО АКТУАТОРА

Крживка Владимир

докторант кафедры электроэнергетики

Чешского технического университета в Праге,

 г. Прага

Е-mail: krivkvla@fel.cvut.cz

Данная статья была написана в ходе работе по гранту: GACR P102/11/0498.

В данной статье рассматривается математическая модель однонаправленного трехфазового актуатора (линейного привода), его принцип работы, его числовое решение с использованием рабочих параметров и характеристик для различных значений тока возбуждения, приводятся полученные результаты и указывается дальнейшее направление работы.

Во многих сферах промышленности используются устройства с перемещением по точным координатам, работа которых основана на механических, пневматических, гидравлических принципах и, как правило, требующая дополнительное (газовое, масленное, водное) оснащение.

К рассмотрению предлагается иной способ достижения перемещения на плоскости: изменение электромагнитного поля во времени. Управление движением будет осуществляться через изменение величины возбуждающих токов с постоянной частотой 50 Гц. На рисунке 1 приведены два варианта конструкции устройства.

Как видно из рисунка 1, в канавках магнитной цепи 1, которые могут находиться либо в одной или в обеих частях схемы, находятся трехфазные или многофазные обмотки 2. Актуатор работает в немагнитной среде, предпочтительно в воздухе. Между нижней и верхней частями магнитной цепи находится электропроводящая, но немагнитнопроводяющая пластина 3 (например, из алюминия), которая под воздействием электродинамических сил левитирует и может перемещаться в направлении оси  [3, c. 1].

Рисунок 1. Варианты конструкции призматичного актуатора [3, c. 1]
(слева — с простой обмоткой, справа — с двойной обмоткой)
1 —магнитная цепь; 2 — трехфазные (многофазные) обмотки;
3 — электропроводящая, но немагнитнопроводяющая пластина

Гармонические токи, протекающие через обмотки 2 в магнитной цепи 1, создают изменяющееся магнитное поле, являющееся типичным представителем бегущей волны. Это поле создает в пластине 3 ток почти в противоположеном направлении (т. е. сдвиг практически на 180°) относительно возбуждающих токов (рисунок 2).

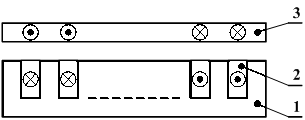
Рисунок 2. Возбуждающие токи и токи индуцированные в проводящей пластине [3, c. 1]

В результате взаимодействия между магнитными полями, созданными токами возбуждения, и токами, индуцированными в пластине, возникает сила , которая состоит из двух компонентов:  и .

Компонент  — сила отталкивания пластины от магнитной цепи (т. е. в направлении по оси ). При условии, что >(гравитационная сила пластины), пластина может свободно левитировать в зазоре магнитной цепи. Пластина будет перемещаться по оси , когда компонент ≠0 (рисунок 3).

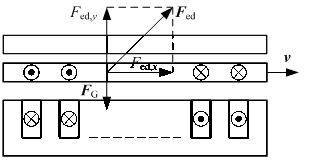
Рисунок 3. Силы в системе [3, c. 2]

Построение математической модели устройства основывается на численном решении для его характеристик и эксплуатационных параметров при различных амплитудах. Ограничивающими условиями являются значения температур обоих проводников обмотки возбуждения и самой пластины, данные температуры с учетом использования изоляционного материала не должны превышать 200°C [3, c. 2].

Решение поставленной задачи не может обойтись без введения ряда упрощений. Главным из них является игнорирование третьего размера, а именно, пренебрегая влиянием краевых эффектов в направлении оси , принимаем, что актуатор в направлении данной оси имеет бесконечную длину, и решение задачи будет проведено в плоскости .

Другим упрощающим предположением является то, что относи­тельная проницаемость магнитной цепи является постоянной. Благодаря воздушному зазору в системе, который приводит к более высокому магнитному сопротивлению магнитного пути, значение магнитного насыщения железа не слишком высоко и находится в линейной части характеристики намагничивания. Введение данного упрощения поможет предотвратить возникновение большой ошибки в расчетах.

Предположение, что пластина перемещается только направлении  практически удовлетворяет действительности, поскольку магнитная цепь покрыта веществом с низким коэффициентом трения, таких, как тефлон, с наличием узкого воздушного зазора, следовательно, наклон пластины в воздушном зазоре маловероятен.

Уравнения движения плиты могут быть записаны в виде [4, c. 286]

,                                    (1)

где:  — скорость пластины в направлении ;

 — вес пластины;

 — сумма внешних сил, действующих в направлении .

Начальные условия для системы уравнений (1) будут выглядеть следующим образом

.                                      (2)

Член  состоит из электродинамической силы вождения  и, как правило, нескольких пассивных сопротивлений, действующих против .

Сумму всех электродинамических сил, действующих на пластину, найдем с помощью интегрирования объемных сил по всему объему пластины в соответствии с уравнениями

                                (3)

Одно из пассивных сопротивлений, действующих против , состоит из сопротивления трения, вызванного на поверхности магнитной цепи (которая покрыта скользящим изоляционным слоем), и имеет значение равное

 ,                                                      (4)

где:  — суммарная сила, которая толкает пластину на верхнюю или нижнюю части магнитной цепи. Эта сила возникает при сложении силы тяжести пластины и -компоненты электродина­мической силы .

Другое пассивное сопротивление равно аэродинамическому, действующему в направлении противоположном движению пластины. Данное сопротивление может быть определено из соотно­шения [4, c. 286]

,                                            (5)

Где:  — плотность воздуха;

 — размер передней поверхности пластины;

 — коэффициентом сопротивления.

После подстановки в (1), получим систему из двух нелинейных дифференциальных уравнений, которые необходимо решить численно.

Приведем наглядный пример, целью которого является оценка следующих зависимостей:

1. суммарной электродинамической силы, действующей на пластину в направлении оси  от положения пластины;

2. суммарной электродинамической силы, действующей на пластину в направлении оси  от положения пластины;

3. суммарной электродинамической силы, действующей на пластину в направлении оси  от значения плотности тока в возбуждающих обмотках (катушках);

4. положения подвижной пластины актуатора от времени;

5. скорости движущейся пластиной актуатора от времени.

С учетом допущений, значения, полученные в программе Agros2D [2], [5], расчитаны на 1 м длины по оси z. Таким образом, задача решена как двумерная с небольшими погрешностями. Геометрическое решение трехфазного актуатора показано на рисунке 4, а итоговая конфигурация трехфазовой обмотки — на рисунке 5. Список строительных материалов вместе с их физическими свойствами приведены в Таблице 1.

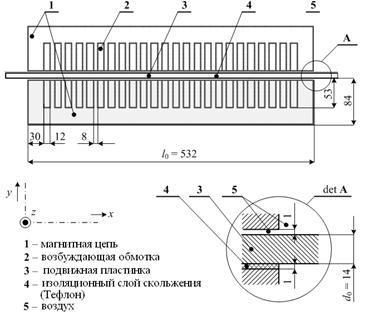
Рисунок 4. Геометрическое решение трехфазного актуатора [1, c. 3740]

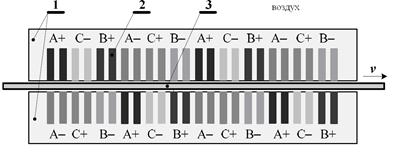
Рисунок 5. Конфигурация трехфазовой обмотки [1, c. 3740]

Вначале в программе Agros2D [2], [5], создается схема актуатора в соответствии с рисунком 5, после этого определяются области (рисунки 4 и 5) с физическими свойствами, приведенными в Таблице 1, затем плитка пошагово (шаг равен 0,004 м) пропускается в зазоре так, чтобы каждая канавка попала, по крайней мере, на три таких шага. После расчетов записываем значение суммарной электродинамической силы, действующей на пластину в направлении оси  при различных токах трехфазовой обмотоки (см. рисунки 6—9). Для автоматизации и ускорения расчетов был создан сценарий в программе Python Lab.

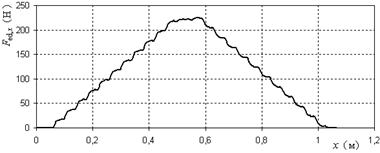
Рисунок 6. Зависимость суммарной электродинамической силы, действующей на пластину в направлении оси x от положения пластины при нулевой скорости и плотности тока 4 А/мм2

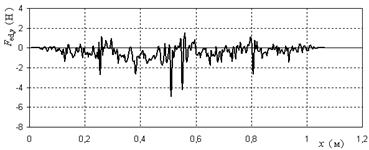
Рисунок 7. Зависимость суммарной электродинамической силы, действующей на пластину в направлении оси y от положения пластины при нулевой скорости и плотности тока 4 А/мм2

Таблица 1.

Физические свойства использованных материалов [1, c. 3742], [3, c. 18]

^* скорректировано относительно коэффициента заполнения

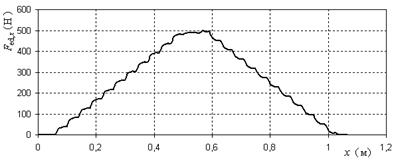
Рисунок 8. Зависимость суммарной электродинамической силы, действующей на пластину в направлении оси x от положения пластины при нулевой скорости и плотности тока 6 А/мм2

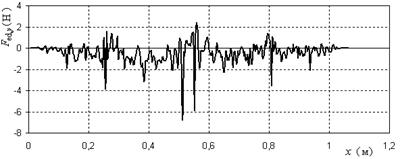
Рисунок 9. Зависимость суммарной электродинамической силы, действующей на пластину в направлении оси y от положения пластины при нулевой скорости и плотности тока 6 А/мм2

Из рисунков 8 и 9 видно, что суммарная электродинамическая сила, действующая на пластину по оси , имеет колебательный характер, что объясняется наличием числовой погрешности программы. В идеальном варианте эта сила близка к нулю, и, в сравнении с силой тяжести пластины (204,6 Н), пренебрежимо мала, поэтому, при нахождении следующих зависимостей: позиции пластины от времени и скорости пластины от времени, можно данной силой пренебречь.

Далее представлена зависимость максимальной электродина­мической силы, действующей на пластину по оси х, от плотности тока (рисунок 10). Вид зависимости близок к квадратичной, что связано с тем, что значение магнитного насыщения магнитной цепи находится в линейной части характеристики намагничивания. С увеличением насыщения магнитной цепи (в нелинейном случае), эта зависимость не увеличивается квадратично, а медленнее. Линейный случай обеспечивает максимально возможное значение силы и параметров движения (скорость) пластины в актуаторе.

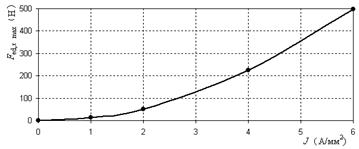
Рисунок 10. Зависимость максимальной электродинамической силы, действующей на пластину по оси x, от плотности тока

На рисунке 11 показаны значения магнитного поля актуатора, рассчитанные в программе Agros2D [2], [5], при положении пластины на расстоянии  м по оси х при плотности тока  А/мм² в обмотке трехфазового актуатора.

Рисунок 11. Значения магнитного поля актуатора при положении пластины на расстоянии 0,3 м по оси х при плотности тока 6 А/мм2

Расчитаем зависимости положения пластины на оси абсцисс от времени и скорости пластины по оси х от времени при различных плотностях тока.

Зависимость скорости пластины от времени определяется из соотношения [4, c. 18]

,                      (6)

где:  — скорость пластины (м/с) в момент времени ;

 — скорость пластины (м/с) в момент времени ;

 — суммарная электродинамическая сила, действующая на пластину в направлении оси  в момент времени  (в положении пластины ), значение находим из рисунка 6 или 8, в зависимости от значения плотности тока;

 — вес пластины ( кг);

 — коэффициент трения ();

 — плотность воздуха (кг/м³ при температуре °C);

 — размер передней панели пластины (м²);

 — коэффициент аэродинамического сопротивления ();

 — начальная скорость пластины ( м/с);

 — разница времени ;

 — количество шагов расчета.

Положение пластины во времени  можно определить по формуле [3, c. 19]:

,                                               (7)

где:  — положение пластины в момент времени ;

 — положение пластины в момент времени ;

 — начальное положение пластны ( м);

На рисунках 12 и 13 представлены зависимости положения пластины и скорости пластины по оси х от времени при плотностях тока равных 4 и 6 А/мм² и начальных условиях, которые перечислены выше.

Рисунок 12. Зависимость положения пластины от времени при различных плотностях тока

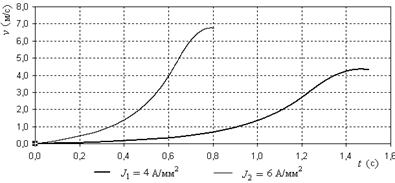
Рисунок 13. Зависимость скорости пластины по оси х от времени при различных плотностях тока

В заключение необходимо сказать, что на данном этапе не было рассмотрено влияние других факторов, например, частота тока возбуждения, толщина подвижной пластины, ширина воздушного зазора и т. п. Поскольку задача представляет собой комплекс взаимосвязанных проблематик, характеризующихся взаимодействием магнитного и температурного полей, объясняющееся тем, что потеп­ление различных частей оборудования приводит к изменению их физических параметров (например, электропроводности или прони­цаемости), которые могут повлиять на распределение магнитного поля, в будущем планируется рассмотреть поле термоупругих деформаций, и как его следствие изменение геометрического решения актуатора.

Также необходимо заметить, что расчет зависимостей положения пластины на оси х и скорости пластины по оси х от времени при различных плотностях тока в соответствии с уравнениями (6) и (7) выполнен с использованием метода Эйлера, который требует большое количество времени для расчета, поскольку величина шага должна быть очень маленькая и, соответственно, количество шагов достаточно велико для поддержания требуемой точности расчета. В связи с этим, в дальнейшем, планируется использовать метод Рунге-Кутты, так как при большей величине шага (количество шагов меньше) точность расчета такая же, как в использованном методе, а время, затраченное на расчет значительно меньше.

Кроме указанных факторов, влияющих на точность расчетов, к ним можно отнести и то, что расчет силы проводился при нулевом значении скорости, хотя на каждом шагу величина менялась, поэтому на следующих этапах работы планируется вести расчет силы при актуальном значении скорости.

Список литературы:

1.Doležel, I., Donátová, M., Karban, P., Ulrych, B. Coupled Analysis of a 3-Phase Linear Actuator// In ICEMS 2008: Proceedings of the 11th International Conference on Electrical Machines and Systems (October, 2008). — Wu-han, China, 2008. — p. 3740—3745.

2.Karban P. et al: Agros2D-an application for the solution of physical fields. [Электронный ресурс]. — Режим доступа: http://agros2d.org (дата обращения 15.11.2012).

3.Křivka V., Modelování trojfázového aktuátoru: odborná studie. — ČVUT, FEL v Praze, Praha, 2012.

4.Křivka V., Electromagnetic damping system with three permanent magnets// Acta Technika, 2012.Vol. 57. № 3. — P. 283—294.

5.Šolín P. et al: Hermes2D-higher-order modular finite element system. [Электронный ресурс]. — Режим доступа: http://hpfem.org (дата обращения 19.11.2012).