КОСМОЛОГИЧЕСКАЯ МОДЕЛЬ С К-ЭССЕНЦИЕЙ ПРИ ПЛОТНОСТИ ρ_m=aⁿ

Ертилиева Айнур Балыкбаевна

магистрант, Евразийский национальный университета имени Л. Н. Гумилева г. Астана, Казахстан

Ержанов Кобланды Канаевич

канд. физ.-мат. наук, доцент Евразийский национальный университет имени Л. Н. Гумилева, г. Астана, Казахстан

E-mail

1.ВВЕДЕНИЕ

Темная энергия стала одним из важнейших вопросов современной космологии с тех пор, как наблюдения сверхновых типа Ia впервые показали, что во Вселенной происходит ускоренное расширение [2, c. 1022]. Тем не менее, до сих пор, мы все еще мало знаем о темной энергии. Темная энергия практически равномерно распределяется во Вселенной, и ее давление отрицательное. Самый простой и теоретически существенной величиной темной энергии является энергия вакуума (или космологическая постоянная Λ) с постоянным параметром состояния . За последнее десятилетие были предложены многочисленные модели темной энергии, например, квинтэссенция, фантомное поле, к-эссенция, тахионы (обобщенные), Чаплыгин газ, и т. д.

Идеей о к-эссенции является идея о том, что неизвестный компонент темной энергии обусловлен минимально связанным скалярным полем φ с неканонической кинетической энергией, что приводит к отрицательному давлению [1, с. 572]. К-эссенция получила много внимания, и первоначально была предложена в качестве модели инфляции, а затем в качестве модели для темной энергии. Действие имеет вид:

                            (1.1)

Это общее поле включает в себя Лагранжиан как частные случаи общей канонической модели скалярного поля, DBI-инфляции и к-эссенции. В ряде случаев, к-эссенция не может экспериментально отличатся от квинтэссенции [3, c. 1877].

После того как была предложена эта модель, к-эссенция интенсивно изучается. В этих моделях рассматриваются различные наблюдаемые величины, такие как давление темной энергии и величина к-эссенции.

2.КРАТКИЙ ОБЗОР КИНЕТИЧЕСКОЙ К-ЭССЕНЦИИ

Будем исходить из следующего действия для кинетической к-эссенции

                             (2.1)

где  плотность вещества Лагранжинана. Здесь  Лагранжиан к-эссенции, который зависит от безразмерной величины X:

                                                  (2.2)

Такие теории были использованы в качестве моделей инфляции и темной энергии, например, кинетическая к-эссенция или духовый конденсат. Простейший нетривиальный пример кинетической к-эссенции является Лагранжиан духового конденсата

                                                  (2.3)

который был также изучен в контексте объединения темной материи / энергии. Другой пример происходит от описания Дирака-Борна-Инфельда для D-браны в струнной теории со скаляром Борна-Инфельда типа в Лагражиане.

                                                   (2.4)

Тензор энергии-импульса получается из (1.1) и имеет форму идеальной жидкости,

  (2.5)

здесь

                                                    (2.6)

где η=+1 или -1 в зависимости от того, положительный или отрицательный φ₀.

Соответсвующие гидродинамические величины

                                               (2.7)

И параметр уравнения состояния

                                                          (2.8)

3. РЕШЕНИЕ

Рассмотрим метрику Фридмана - Леметра - Робертсона -Уокера

                                   (3.1)

где  космическое время. Для этой метрики уравнение движения принимают вид:

                                                (3.2)

                                          (3.3)

                                    (3.4)

                                                (3.5)

                                                         (3.6)

В нашем случае возмем, что плотность  следующим образом зависит от масштабного фактора:

.                                                               (3.7)

Находим

 .                                                    (3.8)

Подставляем в (3.5) и находим :

 .                                            (3.9)

Отнимаем уравнения (1.2) и (1.3) друг от друга и получим следующее выражение:

.                           (3.10)

Так как

 .                                             (3.11)

В уравнение (3.10) подставляем выражения для , ,и находим

 .                        (3.12)

Суммируем уравнения (1.2) и (1.3). Получится следующее уравнение:

 .                              (3.13)

Подставляем сюда выражения для , , , а также выражения из уравнения (3.6) и находим

 .                                   (3.14)

Найденное выражение для  подставляем в (3.12)

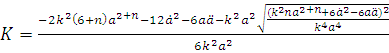 .                         (3.15)

Таким образом у нас получились выражения для  и , которые зависят только от масштабного фактора.

Так, если принять что:

                                                         (3.16)

Тогда они будут иметь следующий вид:

                                     (3.17)

и

                                                      (3.18)

4. ЗАКЛЮЧЕНИЕ

В данной работе мы исследовали модель к-эссенции для случая когда плотность . Найдена зависимость выражения для к-эссенции от масштабного фактора. Как частный случай для демонстрации результатов было получено точное аналитическое выражение для величин  и  для случая, когда масштабный фактор равен .

Список литературы:

1.Perlmutter, S., et al. Supernova Cosmology Project Collaboration / Perlmutter, S., et al. // Astrophys. J. – 1999. № 517. – P. 565–586.

2.Riess A. G., et al. Supernova Search Team Collaboration / Riess A.G. et al. // Astron. J. – 1998. № 116. – P. 1009–1038.

3.Tsyba P. Yu., Kulnazarov I. I., Yerzhanov K. K., Myrzakulov M., Pure kinetic k-essence as the cosmic speed-up and F(T)-gravity // Int. J. Theor Phys. – 2011. № 50. – P. 1876–1886.