CТОХАСТИЧЕСКИЙ САМОПРОИЗВОЛЬНЫЙ ВЫПЛЕСК КЛАСТЕРОВ В КОЛЛОИДНОЙ СИСТЕМЕ ОКСИГИДРАТА ЖЕЛЕЗА (III) И ИЗМЕНЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВО ВРЕМЕНИ

Кузнецов Александр Львович

аспирант, ФГБОУ ВПО «ЧелГУ», г. Челябинск

Сухарев Юрий Иванович

д-р хим. наук, профессор ФГБОУ ВПО «ЧелГУ», г. Челябинск

Тарамина Евгения Викторовна

аспирант, ФГБОУ ВПО «ЧелГУ», г. Челябинск

e-mail: alchemicalchelgu@yandex.ru

В работах [14, 11, 4] впервые показано самопроизвольное появление электрического потенциала в оксигидратныхгелевых системах на углеграфитовых или платиновых электродах как следствие спайкового выброса заряженных кластеров. Авторами [12] установлен пульсационно-периодический характер токовыхнановыплесков. Согласно особенностям изменения СПТ (самопроизвольный пульсационный ток) во времени можно выделить определенные временные интервалы возраста образцов.

Появление спайковогонанотока обусловлено бифуркационными явлениями разрушения нанокластерных орбит колебательного движения. Создание аттракторных альбомов [15] периодического движения в оксигидратных гелях дает возможность проанализировать характер коллоидных бифуркаций в экспериментальной системе, то есть в конечном итоге механизм коллоидно-химических реакций.

Теоретический анализ

Введение рэтчет-потенциала в теории динамических систем [15, 1] позволяет понять и смоделировать стохастические внешние силы или, в общем случае, стохастические изменения реакций кластеров в условиях неравновесного перехода. При рассмотрении работы рэтчетов необходимо ввести некий элемент нарушения симметрии для выбора направленного движения броуновских кластеров. Это нарушение симметрии обычно вводится путем выбора периодического, но ассиметричного потенциала, который является пилообразным потенциалом, или рэтчет-потенциалом в среде. Для периодического описания гелевыхоксигидратов под влиянием пилообразныхрэтчетов предложено использовать оператор Лизеганга [12, 15].

Различают два стохастических прототипа рэтчета: качающиеся рэтчеты, в случае странных нехаотических аттракторов (СНА) изменения вязкости и для класса аттракторных структур, различающихся профилем потенциальной энергии; «мигающие» рэтчеты при самопроизвольных спайковых выплесках [1].

Важно то, что эти потоковые взаимодействия бесстолкновительны.Если движущийся кластер находится в ячейке с помехой или помехами, то идет реакция, нуждающаяся в этих помехах (то есть формируются точечно-рефлексные отображения этих взаимодействующих фрагментов, например, каустик, на углеграфитовых электропроводящих пластинах) [1, 2].

Несомненно, для нас важна структура или геометрия каустики. Так как регистрация каустики осуществляется электрически, то следует понять геометрию расположения заряда (или зарядов) на поверхности кластеров в фазовом пространстве, так как токовые аттракторы нами рассматриваются именно в фазовом пространстве. Из общих соображений [2], касающихся особенностей теории Уитни, рассматривающих границы достижимости управления коллоидной системой в фазовом пространстве, имеются точки этого пространства, через которые можно достичь некоторые цели управления, например, определенной формы каустики в кластерном потоке, которая называется областью достижимости. Из известных четырех типов границы областей достижимости три записываются простыми формулами при подходящем выборе локальных координат, а именно:

                                                (1)

Особенность четвертого типа по Арнольду связана с теорией дифференциальных уравнений, неразрешимых относительно производной, называемых неявными дифференциальными уравнениями. Эти уравнения записываются как

                                                                   (2)

где Геометрически уравнение  задает поверхность в трехмерном пространстве с координатами (x,y,p). Образованная поверхность называется поверхностью дифференциального уравнения. Условие  выделяет плоскость в каждой точке этого трехмерного пространства, которая состоит из векторов, причем y–компонента которых в раз больше x–компоненты. При этом p – есть координата точки приложения. Такая плоскость называется контактной. Вертикальные контактные плоскости задают поле контактных плоскостей, и называются контактной структурой. Контактная структура «высекает» на поверхности уравнения поле направлений с особыми точками в тех местах, где контактная плоскость касается поверхности уравнения (нормально расположенная к кластеру и регистрирующая нанотоки графитовая пластина). Поверхность уравнения здесь предполагается гладкой. Ответ на вопрос о строении типичных особых точек неявных дифференциальных уравнений представляется в виде решения следующего уравнения [2]:

.                                                           (3)

В зависимости от значения параметра k возможны три случая. Особая точка поля на поверхности уравнения, описывающего распространение этого кластерного поля, может оказаться седлом, узлом или фокусом. Отображение поверхности уравнения на плоскость (x,y) вдоль оси римеет особенностью складку. В окрестности типичной точки на складке уравнение приводится к нормальной форме Чибрарио [2] ,

                                                                   (4)

При этом все особые точки автоматически попадают на складку. С физико-химической точки зрения особые точки на складке есть некие активные зоны или точки на поверхности кластера, в которых идет стохастическое диссоциативно-диспропорциональное выталкивание в дисперсионную среду гидратированных ионных образований или разрушение слоев Гуи-Штерна, причем нормально расположенных к графитовой пластине. При этом вытолкнутыенанокластеры образуют контактную структуру. Результат работы складывания особенностей представлен на рис. 1.

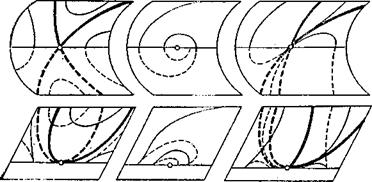
Рис. 1. Теоретически полученные сложенные особенности

На рисунке приведены сложные узоры особенностей, то есть особые точки. Эти особые точки на плоскости () (в нашем случае это электропроводящая графитовая поверхность), называемые сложенным седлом, узлом или фокусом, получены для гелей оксигидрата железа, рис. 2, и представляют собой фазовые портреты оксигидратной системы, которые соответствуют фазовому портрету векторного поля на плоскости вблизи особых точек.

а)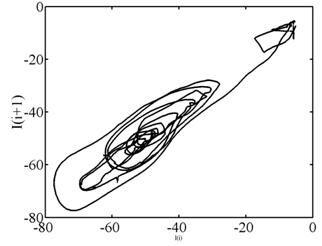б)

Рис. 2. Фазовый портрет оксигидрата железа, время старения 73 сут.,

а) первого возвращения; б) второго возвращения

По Арнольду [2], симплектическая теория имеет контактные аналоги. Например, распространение волн в сплошных средах описывается световой гиперповерхностью в контактном пространстве. Эта гиперповерхность, вообще говоря, имеет особенности Уитни. На трансферсальном к многообразию особенностей трехмерном пространстве световая гиперповерхность оставляет след, диффеоморфный квадратичному конусу  [4]. В коллоидно-химических системах хорошо известен световой конус Тиндаля [13]. Все это звенья одной цепи.

Нами установлены волновые свойства гелевыхоксигидратных систем. Поэтому и свойства волновых стохастических кластерных фронтов должны содержаться или определяться своей гиперповерхностью по отношению к некоей контактной структуре. При этом лучи на линиях тока определяют проекции ее характеристик. Мы наблюдаем своеобразное явление внутреннего бесстолкновительного рассеяния оксигидратных стохастических волн на неоднородностях среды (например, кластерах) и регистрируем это рассеяние в виде фазовых портретов (рис. 2).

Экспериментальная часть

Прибор для измерения импульсного поляризационного электрического тока состоял из прямоугольной ячейки, на концах которой закрепляли графитовые электроды (рис. 3). Контакты электродов подключали к электронному регистрирующему блоку. Свежеприготовленный гель помещали в эту ячейку. Расстояние между электродами составляло 70 мм. При этом ячейка, содержащая гель, замыкалась практически накоротко, величина омического сопротивления системы была незначительной (20 кОм). Электроток, возникающий в системе, замеряли на специальном электронном оборудовании [16, 7, 3] с частотой опроса системы 5 раз в секунду. Эксперимент проводили в течение 5 часов. Процесс термостатировали (Т=303К).

Все токоподводящие шины бронировали от внешних электромагнитных наводок.

Рис. 3. Фотография экспериментальной коллоидно-химической ячейки для снятия спайковых выплесков тока самоорганизации оксигидратных гелей

Исследовали в работе влияние времени созревания геля оксигидрата железа в маточном растворе на величину токовых выплесков. Свежеприготовленный гелеобразный осадок получили из реактива марки (ч.д.а.) концентрации 0.05М. Раствор получали в большой емкости (5 л) и затем добавления 0.1 N раствор едкого натра. Затем гель выдерживали в маточном растворе при очень медленном перемешивании в течение 73 суток. Для исследования изменения тока в системе гель оксигидрата железа в количестве 10 мл отбирали ежесуточно из реактора и помещали в электрохимическую ячейку.

В процессе синтеза контролировали рН раствора и доводили его до заданного значения, то есть рН 7,0—7.5. Условия синтеза и оптимальные значения рН выбирали на основании рекомендаций, приведенных в работах [16, 12].

Далее оксигидрат железа на разных стадиях старения помещали в систему коаксиальных цилиндров в объеме 10 мл и подвергали механическому сдвиговому воздействию в ротационном вискозиметре «Rheotest – 2» в условиях термостатирования при температуре Т=303±0,5 К, либо в электрохимическую ячейку для замера тока самоорганизации также при температуре Т=303±0,5 К. Скорость сдвига в приборе «Rheotest – 2» составляла 1,4 м/с.

Снятие приборных показаний в обоих случаях проводили автоматически в течение пяти часов при помощи аналогово-цифрового преобразователя Е-270 с частотой опроса исследуемых систем 5 раз в секунду. Эксперименты проводили в течение 3-х месяцев с целью определения более полного характера старения оксигидрата железа во времени.

Результаты и их обсуждение

Расчетные результаты синхронных экспериментов представлены в виде фазовых портретов в табл. 1. Для токовых выбросов аттракторы приводятся в координатах I(i+1)−I(i); I(i+3)−I(i+2)_I(i+2)−I(i+1)_I(i+1)−I(i), для изменения динамической вязкости A(i+1)−A(i); A(i+3)−A(i+2)_A(i+2)−A(i+1)_A(i+1)−A(i), гдеI(i), A(i) - амплитуды соответственно токовых выбросов и динамической вязкости в моменты времени (i), (i+1), (i+2), (i+3).

Полуразмерыобластей структурирующего взаимодействия ГОЖ, рассчитанные по данным спайкового выброса кластеров, а также по данным изменения динамической вязкости приведены на рис. 4 (а, б). Расчет величины кластерных взаимодействий проводили по уравнению

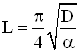,                                                            (5)

где частотная характеристика колебательного движения, - линейный размер кластерного взаимодействия ГОЖ [10]. Этот параметр нами введен, имея ввидуколебательный характер перемещающихся реакционно-активных кластеров и, этот симплекс близок размерам кластерных частиц, но в общем случае их превышает.

а)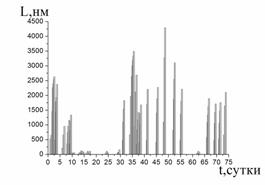б)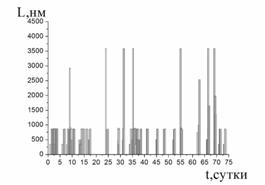

Рис. 4. Полуразмер области структурирующего взаимодействия ГОЖ по данным спайкового выброса кластеров (а) и по данным изменения динамической вязкости, скорость 2,7 с^-1 (б)

В наших работах и работах других авторов показано, что для коллоидных кластерных систем бичастичные взаимодействия кластеров не характерны, запрещены [10]. При этом обязательно должна появиться третья частица (как правило, легкоподвижная), которая диссипирует энергию по объему системы пространственно определенным образом, тем самым делая эту структурную организацию энергетически выгодной. Эти частицы (нанокластеры) формируются в процессе деструкции бидендатно взаимодействующих макромолекул оксигидрата по механизму формирования третьих кластеров, который заключается в диссоциативно-диспропорциональном разрушении макромолекул геля [15, 13, 10].

Так как при этом возникают относительно небольшие заряженные кластеры, то они способны перемещаться в пространстве коллоидной среды по определенным линиям тока при формировании в геле локальной разности потенциалов в условиях, далеких от равновесия. Если перпендикулярно движению кластеров поставить электропроводящие графитовые пластины, то возникающие токовые рефлексы можно отобразить в виде колебательного уравнения (оператора) Лизеганга.Фазовая диаграмма в этом случае принимает вид фазовой паутины Заславского [15, 9].

Таблица 1.

Фазовые портреты гелей оксигидрата железа (III), вычисленные по стохастическому спайковому выплеску кластерных потоков, а также по колебательному изменению динамической вязкости

Отметим, что важный случай C=0 на рис. 5 представлен границами квадратов. Эта единственная фазовая линия, соединяющая несколько диаграмм, представляет собой линии сепаратрис.

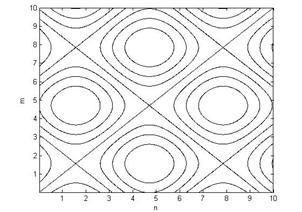
Рис. 6. Графики фазовой зависимости 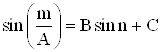 при разныхC, где A=1, B=1.

Подобная форма паутины и обнаружена нами в эксперименте на рисунках табл. 1 для стохастических нанокластерных выплесков. Так как у образцов геля состаренного до 30 суток периоды колебаний меньше, чем для гелей с большим временем старения, то на рисунках отображены лишь точки седел, узлов или фокусов. То есть гель в этой временной области представляется как система с относительно спокойным (гомофазным)структурным континиумом. Начиная с 30-х суток структурная организация геля ГОЖ резко меняется и переходит в область складок Уитни. Эта область охватывает интервал 30—41 сутки. При этом фазовые портреты ГОЖ, полученные по токовым кластерным выплескам, приобретают вид линейных предельных циклов, иногда с выраженными языками Арнольда. На 31, 45, 68, 71 сутки форма фазовых портретов трансформируется в квадраты. Если отображение при некоторых значениях параметров перестает быть обратимым, то тор T³ разрушается. Это соответствует самопроизвольной (почти мгновенной) хаотизации системы. Формирующийся хаос затем практически мгновенно принимает форму тора или предельного цикла.

Область 13—30 суток соответствующая точечным рефлексам объясняется следующим образом. Эволюция подобных сложных систем описывается системой  обыкновенных дифференциальных уравнений

,                                                     (6)

где X - вектор из (фазового пространства), а F- векторное поле над этим пространством. Так как мы строим сечения Пуанкаре, то если сечение тор, имеются две константы f₁,f₂, определяющие перемещение нанокластеров по поверхности тора. При этом сечение Пуанкаре есть замкнутая кривая C. Хотя кривая  непрерывна, последовательные точки пересечения траектории с углеграфитовой плоскостью  не покрывают ее сплошь, но покрывают ее так, как это следует в области 13—30 суток. Между f₁и f₂ на торе возникает затягивание частоты: отношение f₁/f₂ равно отношению двух целых чисел n₁ и n₂. Завершив n₁ оборотов по «параллелям» и n₂ оборотов по «меридианам» тора, траектория замыкается. То есть мы действительно имеем дело с периодическим решением с периодом . При этом сечение Пуанкаре содержит только n₁ точек, для которых .

Область 1—9 суток объясняется еще практически отсутствием аттракторных (притягивающих) образований. Агрегация же частиц носит поверхностный, Ван-дер-Ваальсовский характер. Это скорее когезия.

В процессе старения гелей, в процессе их конденсации трансформация подобных фазовых портретов, механизмов их реализации меняется во времени. Причем темп изменения характера фазовых портретов в процессе временной конденсации убыстряется. Это отчетливо следует из табл. 1.

Оксо-оляционная полимеризация геля ГОЖ, ее глубина хорошо прослеживается при исследовании периодического изменения динамической вязкости ГОЖ. Геометрический характер аттракторов изменения динамической вязкости представлены в таблице 1. Рассмотрение геометрии фазовых аттракторов изменения динамической вязкости позволяет выделить два структурных этапа. При сдвиговой скорости 1.4 м/св области 1—40 суток геометрия аттракторов имеет форму квадратов. Как следует из литературы [5], эта геометрия известна как геометрия конвективных валов, рис. 6. При возникновении валов распределения скорости не зависит от одной из координат. Задачу следует считать двумерной. При возрастании конденсации в системе вследствие полимеризации конвективные валы начинают отчетливо колебаться и разрушаться [5]. Это явление визуально отмечается после 40 суток старения.

Рис. 6. Гидродинамические валы коллоидно-химической системы ГОЖ

Начиная с 40 суток система переходит в сугубо турбулентный режим, который характеризуется высокой завихренностью системы, хорошо прослеженной на рисунках таблицы 1. Переход к хаосу в этом случае осуществляется вследствие полимерно-геометрического изменения (увеличения) оксигидратных кластеров на фоне турбулизации потока.

Если более внимательно взглянуть на геометрию фазовых портретов изменения динамической вязкости, то можно выделить следующие временные этапы изменения формы конвективных валов: 1—30 суток (отмечается область выраженных изменений 13-30); затем следуют временные интервалы (30-41); (41- 53; 53-62 -71). Практически идентичные интервалы областей старения обнаружены и на фазовых портретах стохастического выброса кластеров оксигидрата железа. Это следующие области: (1-13 (15) суток; 13-29 (31); (31 - 38 (41,45)) суток; 38 -((41,45,48) - 52); (52 – 66) суток. То есть отмечается полная корреляция фазовых портретов стохастического выброса кластеров с фазовыми портретами изменения динамической вязкости, построенных в условиях конвективного течения геля при его оксо-оловой полимеризации.

Выводы

1.    В работе механизм диссоциативно-диспропорционального разрушения макромолекул геля.

2.    Анализ контактной структуры или формы паутины позволил обнаружить области с характерными структурными особенностями фазового пространства системы на разных этапах старения геля оксигидрата железа.

3.    Оксо-оляционная полимеризация ГОЖ, ее глубина прослеживаются при исследовании периодического изменения геометрии фазовых портретов, изменения динамической вязкости ГОЖ.

4.    Фазовые портреты стохастического выброса кластеров оксигидрата железа и изменения динамической вязкости геля существенно различаются по своей геометрической форме, но имеют практически идентичные интервалы областей старения.

Список литературы:

1.Анищенко В. С., Астахов В. В., Вадивасова Т. Е. и др. Нелинейные эффекты в хаотических и стохастических системах. Москва-Ижевск: Институт компьютерных исследований.2003. - 529 с.

2.Арнольд В. И. Теория катастроф. Изд. 4-е, стереотипное. – М.: Едиториал УРСС,2004.128 с.

3.Волович Г. И. Схемотехника аналоговых и аппаратно-цифровых электронных устройств. М.: Изд. Дом “ Додека-ХХI”, 2005. - 528 с.

4.Егоров Ю. В. Статика сорбции микрокомпонентов оксигидратами. М.: Атомиздат. 1975. - 218 с.

5.Малинецкий Г. Г., Потапов А. Б. Современные проблемы нелинейной динамики.-М.: УРСС, 2002. - 358 с.

6.Марков Б. А., Сухарев Ю. И., Лебедева И. Ю., Апаликова И. Ю. Аналитическое определение размеров области структурирующего взаимодействия заряженных оксо-оловых кластеров. Журн. Бутлеровские сообщения.2010.Т.19. № 2. С. 62—69.

7.Паспорт 422272-270-42885515 ПС. Носитель преобразований многофункциональный Е-270. Москва, ЗАО «Л-КАРД».

8.Рейнтен Х. Т. Строение и свойства адсорбентов и катализаторов. М.:1973. - 322 с.

9.Слабый хаос и квазирегулярные структуры/ Заславский Г. М., Сагдеев Р. З., Усиков Д. А., Черников А. А.- М.: Наука. 1991. – 235 с.

10.Суздалев И. П. Нанотехнология: Физико-химия нанокластеров и наноматериалов.-2-е изд., испр.-М.:URSS,2008. - 589 с.

11.Сухарев Ю. И., Марков Б. А. Нелинейность гелевых оксигидратных систем. Екатеринбург: УрОРАН. 2005. - 468 с.

12.Сухарев Ю. И. Синтез и применение специфических оксигидратных сорбентов. М.:Энергоатомиздат.1987.120 с.

13.Фридрихсберг Д. А. Курс коллоидной химии. М.:Наука.1974. - 378 с.

14.Sucharev Yuri I. Nonlinearity of Colloid Systems: Oxyhydrate Systems. Switzerland, UK, USA: Trans Tech Publications. 2007. – 433 p.

15.Sucharev Yuri I. Wave Oscillations in Colloid Oxyhydrates // Switzerland, UK, USA: Trans Tech Publications LTD.2010. - 497 p.

16.Sukharev Yu. I., Markov B. A., Prokhorova A. Yu., Lebedeva I. Yu. Spontaneous pulsating current in zirconium oxyhydrate gels. Wseas transactions on circuits and systems.2005. Vol.4. No. 11. P. 1109—2734. P. 1477—1484.