О МЕХАНИЗМЕ ЭЛЕКТРОЛЮМИНЕСЦЕНЦИИ ДИОДОВ НА БАЗЕ SI:ER ПРИ ОБРАТНОМ СМЕЩЕНИИ

Зимовец Инна Анатольевна

аспирант, ННГУ, г. Нижний Новгород

E-mail: 

Филатов Дмитрий Олегович

канд. ф.-м. наук, доцент, НОЦ ФТНС ННГУ, г. Нижний Новгород

E-mail: 

Одной из наиболее актуальных задач современной оптоэлектро­ники является создание на базе традиционной кремниевой технологии твердотельных излучающих элементов и фотодетекторов, работающих в области длин волн 1,5 мкм. В самом кремнии отсутствуют свойства, требуемые для получения таких приборов. Кремний является непрямо­зонным полупроводником и эффективность межзонной рекомбинации в нем очень низка. Чтобы при рекомбинации электрона и дырки обра­зовался фотон, должны одновременно выполняться закон сохранения энергии и импульса, то есть энергия фотона должна равняться ширине запрещенной зоны [1].

Есть три способа использовать кремний в электролюминесценции:

Если воспользоваться принципом неопределенности — система ограничена в координатном пространстве — растет неопределенность в величине импульса:

—начинают светиться наночастицы кремния в матрице из оксида кремния, мезопористый кремний (поры — 10 нм), квантовые ямы, проволоки.

1.     При наличие оптической накачки, частота которой выше частоты, соответствующей частоте запрещенной зоны, часть энергии накачки передается кристаллической решетке — образуются фононы.

Это явление — Рамановское рассеяние (Раман, 1928), фононы, образующиеся при Рамановском рассеянии берут на себя тот импульс, который не может унести фотон.

2.     Третий способ — легировать кремний люминесцентными атомами, которые будут светиться в среде кремния — одним из таких активным включением является Er., который формирует в кристал­лической решетке эффективные центры излучательной рекомбинации с участием Si. В спектре люминесценции центра, содержащего трехразрядный ион эрбия, наблюдается узкая температурно-незави­симая линия на длине волны 1,54 мкм, ответствующий минимуму по­терь и дисперсии в кварцевых волокнах. Это позволяет создавать опто­электронные приборы на основе Si :Er и использовать их в системах волоконно-оптических линий связи.

В результате исследований были найдены условия формиро­вания эрбиевых центров в кремнии, обеспечивающих наличие фото- и электролюминесценции на длине волны 1,54 мкм, установлено, что при комнатной температуре интенсивность электролюминесценции (ЭЛ) в диодных структурах Si/Si:Er/Si в режиме пробоя p/n-перехода при обратном смещении заметно превосходит наблюдаемую при пря­мом смещении и сильно зависит от концентраций мелких доноров и акцепторов в активном слое Si:Er. Свойства Si:Er слоев зависят от технологии их получения.

В большинстве работ по эрбиевой электролюминесценции (ЭЛ) в структурах Si/Si:Er/Si с p—n переходом в режиме пробоя при обрат­ном смещении для объяснения наблюдаемых эффектов предполагает­ся, что возбуждение ЭЛ на длине волны l»1,54 мкм в 4f-оболочке ионов эрбия обусловлено передачей им энергии горячими электронами зоны проводимости. представленные в [3]. Для модели [2] зонная диаг­рамма перехода p⁺-Si/n-Si:Er рассчитывалась на базе решения уравне­ния Пуассона:

 ,                                                   (1)

где: j(z) — профиль потенциала для электронов,

e — диэлектрическая проницаемость Si,

e₀ — диэлектрическая постоянная,

е — элементарный заряд,

 ,                    (2)

где:                                                      (3)

— концентрация дырок в валентной зоне,

N_v — эффективная плотность состояний в валентной зоне Si,

F_p — квазиуровень Ферми для дырок,

k_B — постоянная Больцмана,

Т — абсолютная температура,

                                                  (4)

— интеграл Ферми порядка ½,

                                                    (5)

— концентрация электронов в зоне проводимости,

N_с — эффективная плотность состояний в зоне проводимости Si,

F_n — квазиуровень Ферми для электронов. В этом случае решение уравнения Пуассона: ,

где:                                                                                             (6)

— толщина части ОПЗ, приходящаяся на слой p⁺-Si,

V_p — доля контактной разности потенциалов р⁺—n перехода j_c, падающая на ОПЗ слоя p⁺-Si ,

где: V_n — доля j_c, падающая на части ОПЗ, лежащей в слое n-Si:Er,

E_cp и E_cn — энергии дна зоны проводимости в квазинейтральных областях слоёв p⁺-Si и n-Si:Er (области I и IV, соответственно). На границе квазинейтральной области слоя n-Si:Er (z=l_n) условие квазинейтральности записывалось в виде: ,что даёт

(7)

Рассматривался также процесс туннельной инжекции электрона из валентной зоны на глубокий центр с координатой z_d [4] Форма по­тенциальной ямы глубокого центра аппроксимировалась водородоподобной моделью:

,                                                       (8),

где: e_eff = (R_y/E_d)^1/2 — эффективная диэлектрическая проницаемость,

R_y»13,6 эВ — потенциал ионизации атома водорода постоянная Ридберга).

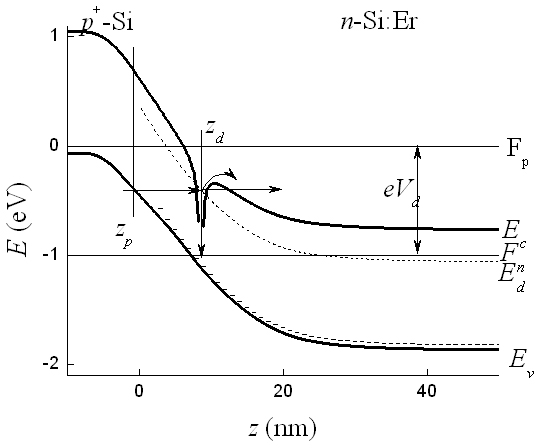
 Рис. 1 Расчётная зонная диаграмма структуры p⁺-Si/ n-Si:Er (300 К) при приложении обратного смещения V_d=1 В. N_Er=3×10¹⁸ cм^—3, E_d=0,3 эВ

При решении системы дифференциальных уравнений в частных производных (PDE) рекомендуется использовать расширение матема­тического пакета Matlab — пакет femlab.

Программное обеспечение выполняет конечноэлементный ана­лиз вместе с адаптивным построением сетки, используя целый ряд чис­ленных решателей. Большой интерес представляет реализация в среде Matlab(femlab) новый тип разностных схем — бикомпактные схемы. Решение задач в слоистых средах сложно тем, что трудно построить аппроксимацию, дающую высокий порядок точности на стыках сред. Если задавать сетку так, что граница сред лежит между узлами сетки, то построить аппроксимацию сложно — приходится выбирать сетку так, чтобы ее узлы попадали на границы слоев (такие сетки назы­ваются специальными). Если шаблон аппроксимации содержит три и более пространственных узла, то специальные сетки не спасают — если внутренний узел шаблона совпадает с границей, то аппрокси­мация производных идет через разрыв коэффициентов — ухудшается точность расчетов. Использование в расчете полуцелых узлов приво­дит к такому же эффекту. Использование бикомпактных схем (шаблон состоит из двух узлов сетки, полуцелые точки в расчетах не участ­вуют) позволяет достигнуть высокой точности расчета.

Список литературы:

1. Андреев А. А., Воронков В. Б., Голубев В. Г., Медведев А. В., Пев­цов А. Б. Влияние термического отжига на интенсивность полосы фотолюминесценции 1,54 мкм в легированном эрбием гидрогенизиро­ванном аморфном кремнии. // Физика и техника полупроводников. — 1999. — том 33. — № 1. — C. 106—110.
2. Кудояров В. Х., Кузнецов А. Н., Теруков Е. И., Гусев О. Б., Кудряв­цев Ю. А. и др. Влияние кислорода на интенсивность фотолюминесцен­ции Er (1.54 мкм) в пленках —Si:H, легированных эрбием. // Физика и техника полупроводников. — 1998. — том 32. — № 11. — С. 1384—1390.
3. Соболев Н. А. Кремний, легированный эрбием — новый полупроводнико­вый материал для оптоэлектроники. // Рос. хим. Общ -ва им. Д. И. Менделеева. — 2001. — № 5—6. — С. 95—102.
4. Шенгуров В.Г., Светлов С. П., Ччалков В. Ю., Максимов Г. А., Красиль­ник З. Ф.и др. Солегирование эрбием и кислородом кремниевых слоев в процессе молекулярно-лучевой эпитаксии. //Физика и техника полупро­водников, — 2001. — том 35.— вып. 8. — С. 954—960.