Статья опубликована в рамках: IV Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 01 февраля 2012 г.)
Наука: Физика
Секция: Физика конденсированного состояния
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ ЗАРЯЖЕНИЯ ДИЭЛЕКТРИКОВ С ДИСКРЕТНЫМ СПЕКТРОМ ЛОВУШЕК
Эбель Андрей Александрович
ассистент кафедры общей математики, ЮУрГУ, г. Челябинск
1. Введение
Эффекты накапливания зарядов наблюдаются практически всегда, когда диэлектрики подвергаются воздействию проникающей радиации. Заряды могут вноситься внутрь диэлектриков облучением их пучками заряженных частиц либо генерироваться в виде электронно-дырочных пар. Радиационное заряжение диэлектриков имеет принципиальное значение при использовании диэлектриков в атомной промышленности и космической технике. Свойства облученных диэлектриков в отношении удержания и переноса зарядов наиболее полно описываются в рамках феноменологической модели Роуза-Фаулера [1, 3, 6]. Однако аналитические и существующие численные решения [2, 7] получены только для вариантов модели с рядом существенных упрощений, таких как пренебрежение дрейфом носителей заряда, равномерная генерация квазисвободных электронов и дырок по объему, однородность внешнего электрического поля, квазинейтральность образца диэлектрика, постоянство во времени спектра ловушек (локализованных энергетических состояний в запрещенной зоне) и другие. Такие приближения не позволяют рассматривать сильно неоднородные процессы, включая радиационный пробой диэлектриков. Данная работа посвящена построению более общей реализации модели Роуза-Фаулера, не связанной с перечисленными ограничениями.
2. Математическая модель
Уравнения кинетики носителей заряда, основанные на модели Роуза-Фаулера, учитывают инжекцию заряда, ионизационное образование электронно-дырочных пар, их взаимную рекомбинацию, захват и освобождение носителей заряда из ловушек, дрейф носителей заряда в созданном ими электрическом поле. В одномерном случае система уравнений модели Роуза-Фаулера имеет вид:
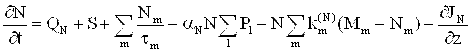 ; (1)
; (1)
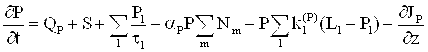 ; (2)
; (2)
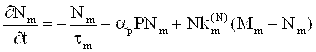 ,
, ![]() (3)
(3)
 ,
, ![]() ; (4)
; (4)
 . (5)
. (5)
Здесь t – время; N, P – концентрации отрицательных и положительных свободных носителей зарядов; ![]() ,
, ![]() – скорости генерации электронов и дырок путем термализации электронов;
– скорости генерации электронов и дырок путем термализации электронов; ![]() – скорость генерации электронно-дырочных пар вследствие ионизации среды (D – мощность дозы,
– скорость генерации электронно-дырочных пар вследствие ионизации среды (D – мощность дозы,
![]() – энергия образования электронно-дырочных пар);
– энергия образования электронно-дырочных пар); ![]() ,
, ![]() – константы рекомбинации отрицательных и положительных носителей заряда;
– константы рекомбинации отрицательных и положительных носителей заряда; ![]() ,
, ![]() – токи, обусловленные движением электронов и дырок;
– токи, обусловленные движением электронов и дырок; ![]() – истинные подвижности электронов и дырок;
– истинные подвижности электронов и дырок; ![]() ,
, ![]() – коэффициенты захвата свободного заряда на ловушках;
– коэффициенты захвата свободного заряда на ловушках; ![]() ,
, ![]() – концентрации ловушек;
– концентрации ловушек; ![]() ,
, ![]() – концентрации захваченных носителей заряда на ловушках;
– концентрации захваченных носителей заряда на ловушках; 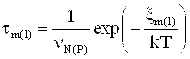 – среднее время жизни захваченного электрона (дырки) в ловушке типа m (l), имеющей энергию
– среднее время жизни захваченного электрона (дырки) в ловушке типа m (l), имеющей энергию ![]() ;
; ![]() ,
, ![]() – частотный фактор;
– частотный фактор; ![]() – напряженность электрического поля; φ – потенциал; е – элементарный заряд; ε – диэлектрическая проницаемость;
– напряженность электрического поля; φ – потенциал; е – элементарный заряд; ε – диэлектрическая проницаемость; ![]() – электрическая постоянная.
– электрическая постоянная.
Скорости термализации и генерации зарядов в общем случае определяются из решения задачи переноса излучения. Спектр ловушек в большинстве материалов может быть аппроксимирован экспоненциальным или гауссовым распределением [4, 7].
Для решения системы уравнений применяется метод разделения по физическим процессам. На первом этапе пренебрегаем дрейфом носителей зарядов под действием электрического поля, и рассматриваем изменение плотности зарядов в течение промежутка времени от ![]() до
до ![]() за счет процессов рождения частиц и рекомбинации. На втором этапе вычисляются эффекты переноса носителей заряда в электрическом поле, в результате чего определяются окончательные значения концентраций частиц в (j+1)-й момент времени. Скорость движения носителей определяется подвижностью носителей и напряженностью электрического поля. На третьем этапе по распределению электронов и дырок в текущий момент времени методом прогонки решалось уравнение для электрического поля (5).
за счет процессов рождения частиц и рекомбинации. На втором этапе вычисляются эффекты переноса носителей заряда в электрическом поле, в результате чего определяются окончательные значения концентраций частиц в (j+1)-й момент времени. Скорость движения носителей определяется подвижностью носителей и напряженностью электрического поля. На третьем этапе по распределению электронов и дырок в текущий момент времени методом прогонки решалось уравнение для электрического поля (5).
3. Численный эксперимент
В первую очередь было проведено сравнение предложенного здесь численного метода для решения уравнений одно- и двухловушечной модели Роуза-Фаулера (1) — (5) для случая однородного облучения с методом Гира [5] и приближенным аналитическим решением [7]. Результаты расчетов полностью совпадают, что свидетельствует о применимости разработанного метода для решения уравнений модели радиационного заряжения диэлектрика. Следует отметить, что разработанный метод экономичнее метода Гира и легче обобщается на случай неоднородного распределения носителей заряда.
Далее была рассмотрена задача с непрерывным спектром ловушек. При численной реализации непрерывный спектр ловушек по энергии заменялся дискретным спектром (кусочно-постоянной функцией) [4, 7]. Участки постоянного значения энергии интерпретируются далее как один тип ловушек с соответствующей энергией и концентрацией. Разбивка диапазона энергии осуществляется так, чтобы концентрации ловушек разного типа (площади под кривой) были равны друг другу. Время жизни захваченного носителя заряда зависит от глубины ловушки (![]() ), частоты попыток освобождения (
), частоты попыток освобождения (![]() ) и температуры (
) и температуры (![]() ):
):  . Феноменологические параметры, константа рекомбинации и коэффициент захвата, в общем случае, для каждого типа ловушек различны. Для упрощения модели полагаем, что они одинаковы.
. Феноменологические параметры, константа рекомбинации и коэффициент захвата, в общем случае, для каждого типа ловушек различны. Для упрощения модели полагаем, что они одинаковы.
При проведении расчетов непрерывный спектр разбивался равномерно по глубине на 100 ловушек. На рис. 1 приведена рассчитанная зависимость от времени проводимости облучаемого диэлектрика для непрерывного однородного облучения (сплошная кривая). Для сравнения пунктиром на график нанесены данные работы [8]. Расчеты выполнены при следующих параметрах: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Наблюдается согласование наших результатов с данными [8].
. Наблюдается согласование наших результатов с данными [8].
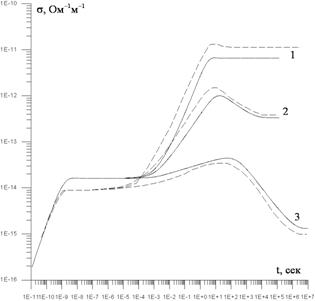
Рисунок 1. Зависимость радиационной проводимости диэлектрика для ![]() (1),
(1), ![]() (2),
(2), ![]() (3).
(3).
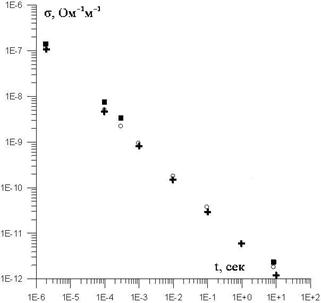
Рисунок 2. Сравнение рассчитанной электропроводности полистирола (маркеры+) с экспериментальными данными (маркеры ■) и с данными работы [4] (маркеры ○).
На временах до ![]() наблюдается рост проводимости из-за преобладания инжекции и генерации частиц над захватом заряда ловушками. В дальнейшем наблюдается плато до
наблюдается рост проводимости из-за преобладания инжекции и генерации частиц над захватом заряда ловушками. В дальнейшем наблюдается плато до ![]() связанное с освобождением заряженных частиц с мелких ловушек. Последующий рост проводимости обусловлен освобождением заряда с глубоких ловушек. На временах более
связанное с освобождением заряженных частиц с мелких ловушек. Последующий рост проводимости обусловлен освобождением заряда с глубоких ловушек. На временах более ![]() наблюдается уменьшение проводимости в связи захватом заряженных частиц на более глубокие ловушки. В последующем на больших временах проводимость выходит на стационарное значение.
наблюдается уменьшение проводимости в связи захватом заряженных частиц на более глубокие ловушки. В последующем на больших временах проводимость выходит на стационарное значение.
Также проводилось сравнение с экспериментальными и расчетными дынными [4] по проводимости полистирола при облучении электронами. Сравнивалось значение проводимости на конец импульса облучения в зависимости от интенсивности облучения (от времени облучения при фиксированной интегральной дозе) (см. рис. 2). Спектр ловушек в материале аппроксимировался также кусочно-постоянной функцией, как это было описано ранее. Как и в [4] была получена зависимость проводимости следующего вида: ![]() .
.
4. Заключение
Численно реализована модель Роуза-Фаулера для случая неоднородного облучения с учетом дрейфа носителей заряда в самосогласованном электрическом поле. Проведено тестирование численного алгоритма путем сравнения с аналитическими, численными и экспериментальными данными других авторов.
Список литературы:
1. Бьюб Р. Фотопроводимость твердых тел. М.: Издательство иностранной литературы, 1962. — 558 с.
2. Ванников А. В., Матвеев В. К., Сичкарь В. К., Тютнев А. П. Радиационные эффекты в полимерах. Электрические свойства. М.: Наука, 1982. — 273 с.
3. Роуз А. Основы теории фотопроводимости. М.: Мир, 1966. — 192 с.
4. Садовничий Д. Н., Милехин Ю. М., Тютнев А. П. Электропроводность неупорядоченных материалов с гауссовым распределением ловушек по энергии // Химия и компьютерное моделирование. Бутлеровские сообщения. 2002. Приложение к спецвыпуску № 10. С. 262 — 266.
5. Самарский А. А., Гулин А. В. Численные методы: учеб. пособие для вузов. М.: Наука, 1989. — 432 с.
6. Сесслер Г. Электреты. М.: Мир, 1983. — 487 с.
7. Тютнев А. П., Ванников А. В., Мингалеев Г. С. Радиационная электрофизика органических диэлектриков. М.: Энергоатомиздат, 1989. — 192 с.
8. Тютнев А. П., Саенко В. С., Пожидаев Е. Д., Костюков Н. С. Диэлектрические свойства полимеров в полях ионизирующих излучений. М.: Наука, 2005. — 453 с.
дипломов

Оставить комментарий