Статья опубликована в рамках: IV Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 01 февраля 2012 г.)
Наука: Физика
Секция: Физика конденсированного состояния
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАГНЕТОСОПРОТИВЛЕНИЕ И ПЪЕЗОСОПРОТИВЛЕНИЕ В КРЕМНИИ р – ТИПА
Таймуратова Лидия Унгарбаевна
канд. физ.-мат. наук, ст. преподаватель, Каспийский государственный университет технологий и инжиниринга имени Ш. Есенова, г. Актау, Республика Казахстан
E-mail: taimuratova@mail.ru
Явление магнетосопротивления состоит, в сущности, в возрастании электрического сопротивления полупроводника (или металла) при помещении его в магнитном поле.
При решении уравнения Больцмана для носителей в электрическом и магнитном полях зависимость ![]() имеет квадратичный вид. Рассматриваемом случае, закон дисперсии отличается от квадратичного и уравнение Больцмана может быть решено только при некоторых приближениях, Лэкс и Мавройдес [5, с. 1651] рассмотрели случай слабых магнитных полей, используя разложение в ряд по степеням
имеет квадратичный вид. Рассматриваемом случае, закон дисперсии отличается от квадратичного и уравнение Больцмана может быть решено только при некоторых приближениях, Лэкс и Мавройдес [5, с. 1651] рассмотрели случай слабых магнитных полей, используя разложение в ряд по степеням ![]() . Рассмотрим кратко метод Макклюра [8, с. 1642], который можно применять в магнитных полях произвольной напряженности. Суть его заключается в том, что скорость дырки, определяющаяся, как
. Рассмотрим кратко метод Макклюра [8, с. 1642], который можно применять в магнитных полях произвольной напряженности. Суть его заключается в том, что скорость дырки, определяющаяся, как ![]() и меняющаяся вдоль орбиты дырки в k- пространстве, разлагается в окрестности пересечения изоэнергетической поверхности и плоскости, перпендикулярной Н, в ряд по степеням
и меняющаяся вдоль орбиты дырки в k- пространстве, разлагается в окрестности пересечения изоэнергетической поверхности и плоскости, перпендикулярной Н, в ряд по степеням ![]() , где
, где ![]() - частота движения по годографу в отсутствие электрического поля. Для большего отклонения изоэнергетической поверхности от сферы следует сохранить большое число членов разложения Фурье (до 5
- частота движения по годографу в отсутствие электрического поля. Для большего отклонения изоэнергетической поверхности от сферы следует сохранить большое число членов разложения Фурье (до 5![]() для тяжелых дырок).
для тяжелых дырок).
Рассмотрим теперь уравнение Больцмана (случай слабого магнитного поля):
|
|
в котором ![]() , а
, а ![]() дается формулой
дается формулой ![]() , сводится к виду
, сводится к виду
|
|
и упрощается подстановкой выражения
|
|
Время релаксации импульса ![]() считаем не зависящим от направления, так как экстремум зоны находится в точке k=0 и имеется симметрия кубической решетки:
считаем не зависящим от направления, так как экстремум зоны находится в точке k=0 и имеется симметрия кубической решетки:
|
|
В случае слабого электрического поля произведениями ![]() на
на ![]() и
и ![]() на
на ![]() можно пренебречь. Произведение
можно пренебречь. Произведение ![]() , поэтому уравнение (2.5.4) принимает вид:
, поэтому уравнение (2.5.4) принимает вид:
|
(1) |
где введен оператор
|
(2) |
Для небольших значений ![]() в первом приближении:
в первом приближении:
|
(3) |
во втором приближении:
|
(4) |
и т. д. Для любого приближения плотность тока ![]() определяется, как обычно, подстановкой величины
определяется, как обычно, подстановкой величины ![]() в выражение:
в выражение:
|
(5) |
где ![]() имеют вид (4) ,(5) и т. д. Феноменологически
имеют вид (4) ,(5) и т. д. Феноменологически ![]() состоит из компонент:
состоит из компонент:
|
(6) |
Из сопоставления коэффициентов следует:
|
|
|
(8) |
где ![]() - тензор перестановки
- тензор перестановки ![]()
![]() , если два индекса одинаковы, и
, если два индекса одинаковы, и
|
(9) |
Если ![]() зависит от
зависит от ![]() , но не зависит от направления k , его можно вынести перед знаком оператора
, но не зависит от направления k , его можно вынести перед знаком оператора ![]() в выражении (2), так как:
в выражении (2), так как:
|
(10) |
где
|
(11) |
Следовательно, в подынтегральных выражениях (10) и (12) ![]() можно вынести из скобок и объединить с имеющимся там множителем
можно вынести из скобок и объединить с имеющимся там множителем ![]() , в результате появятся множители
, в результате появятся множители ![]() ,
,![]() и т. д. Результаты интегрирования в обозначениях, которые использовались в
и т. д. Результаты интегрирования в обозначениях, которые использовались в
|
|
принимает вид
|
|
|
|
|
|
|
|
где ![]() , и так как
, и так как ![]() , то существует продольное магнетосопротивление, которое является следствием гофрированности изоэнергетических поверхностей. Если воспользоваться обозначением
, то существует продольное магнетосопротивление, которое является следствием гофрированности изоэнергетических поверхностей. Если воспользоваться обозначением ![]() символом
символом ![]() с нижним индексом, указывающим кристаллографическое направление, в котором протекает ток, и верхним индексом, указывающим направление магнитного поля, то для магниторезистивного эффекта получаем:
с нижним индексом, указывающим кристаллографическое направление, в котором протекает ток, и верхним индексом, указывающим направление магнитного поля, то для магниторезистивного эффекта получаем:
|
|
Ограничимся этими примерами [6, с. 1530, 7, 5, 2, 3], соответствующими наиболее важным кристаллографическим направлениям.
Для сопоставления этих расчетов и результатов экспериментальных исследований кремния р-типа вклады [9, с. 768, 1, с. 1593] в электропроводность и в магниторезистивный эффект легких и тяжелых дырок складываются по формулам:
|
(17) |
и
|
|
(18) |
соответственно. При вычислении электропроводности вкладом легких дырок можно пренебречь вследствие небольшого их количества, однако в случае магниторезистивного эффекта учет легких дырок совершенно необходим. Предположение, что времена релаксации тяжелых и легких дырок одинаковы, легко обосновать. Любая легкая дырка быстро превращается в тяжелую дырку вследствие рассеяния на колебаниях решетки по двум причинам: 1) избыток энергии легкой дырки уносит фонон, поэтому обратный процесс менее вероятен ![]() , и 2) плотность состояний в подзоне тяжелых дырок больше и, следовательно, вероятность перехода в эту подзону больше вероятности обратного перехода. Однако в случае рассеяния на ионизированных примесях времена релаксации легких и тяжелых дырок различаются. В диапазоне температур, в котором легкие дырки рассеиваются на ионизированных примесях, а тяжелые дырки - на колебаниях решетки, трудно дать удовлетворительное объяснение экспериментальных результатов.
, и 2) плотность состояний в подзоне тяжелых дырок больше и, следовательно, вероятность перехода в эту подзону больше вероятности обратного перехода. Однако в случае рассеяния на ионизированных примесях времена релаксации легких и тяжелых дырок различаются. В диапазоне температур, в котором легкие дырки рассеиваются на ионизированных примесях, а тяжелые дырки - на колебаниях решетки, трудно дать удовлетворительное объяснение экспериментальных результатов.
Валентная зона кремния дважды вырождена в точке экстремума k=0 и поверхности равной энергий имеет довольно сложный вид (деформированная сфера), описываемый формулой:
|
|
|
а при деформационном снятии вырождения ![]() в области малых значений энергии
в области малых значений энергии ![]() может быть выражена следующим образом:
может быть выражена следующим образом:
|
|
|
|
|
|
A, B, C, D – зонные параметры, ![]() ,
,![]() - расщепления валентной зоны при одноосной деформации, определяемые следующим соотношением:
- расщепления валентной зоны при одноосной деформации, определяемые следующим соотношением:
|
|
|
|
|
|
где d и в – константы деформированного потенциала валентной зоны, описывающие относительное смещение по энергии легких и тяжелых дырок при Х║[111] и Х║[001], соответственно.
Из (22) и (23) видно, что изоэнергетические поверхности расщепленных одноосной деформацией валентных зон представляют собой эллипсоиды вращения (а при Х║[110] – трехосное эллипсоиды) с осью вращения, совпадающей с осью деформации, и эффективными массами дырок ![]() для нижней из расщепившихся зон,
для нижней из расщепившихся зон, ![]() для верхней, отщепленной деформацией валентной зоны.
для верхней, отщепленной деформацией валентной зоны.
Основными механизмами тензоэффектов в кремнии р – типа являются:
a) перестройка зонного спектра дырок при сильной одноосной деформации;
b) переселение дырок из верхней отщепленной зоны в нижнюю зону;
c) изменение при деформации относительного вклада различными механизмами рассеяния;
d) изменение при деформации анизотропии рассеяния.
В связи с тем, что при одноосной деформации в валентной зоне кремния происходит коренная перестройка энергетического спектра дырок, то сведения об анизотропии рассеяния дырок могут быть получены только на основе измерений как продольного, так и поперечного (относительно оси деформации) пъезосопротивления.
Наложение сильной одноосной упругой деформации сжатия в валентной зоне кремния, приводит к снятию вырождения в точке экстремума k=0, при этом переселяются носители из зоны легких дырок ![]() в зону тяжелых дырок
в зону тяжелых дырок ![]() , а также происходит перестройка зонного спектра дырок, в обеих зонах (энергетические поверхности принимают вид эллипсоида вращения с осью вращения, совпадающей с осью деформации, и эффективными массами дырок
, а также происходит перестройка зонного спектра дырок, в обеих зонах (энергетические поверхности принимают вид эллипсоида вращения с осью вращения, совпадающей с осью деформации, и эффективными массами дырок ![]() для нижней из расщепившихся зон
для нижней из расщепившихся зон ![]() и
и ![]() для верхней отщепленной деформацией валентной зоны
для верхней отщепленной деформацией валентной зоны ![]() и изменяется анизотропия рассеяния дырок.
и изменяется анизотропия рассеяния дырок.
Благодаря этому исследование только продольного пьезосопротивления не позволяет определить анизотропию подвижности дырок без измерений поперечного пьезосопротивления.
При достаточной деформации практически реализуется одноэллипсоидальная модель (так как все носители сосредотачиваются в зоне ![]() ), следовательно, можно определить параметр анизотропии подвижности следующим образом:
), следовательно, можно определить параметр анизотропии подвижности следующим образом:
|
|
|
где ![]() ,
, ![]() - компоненты эффективной массы и тензора времени релаксации, усредненные по энергии, вдоль и поперек оси вращения эллипсоида, с которой совмещена ось деформирующего усилия.
- компоненты эффективной массы и тензора времени релаксации, усредненные по энергии, вдоль и поперек оси вращения эллипсоида, с которой совмещена ось деформирующего усилия.
Эффективные массы в таких эллипсоидах можно определить по формулам:
|
|
(24) |
|
|
(25) |
Здесь A, B, D – зонные параметры, в и d – константы потенциала деформации, ![]() ,
, ![]() ,
, ![]() - упругие модули,
- упругие модули, ![]() - величина спин-орбитального расщепления.
- величина спин-орбитального расщепления.
В случае смешанного рассеяния, формулу (23) можно записать в виде:
|
|
|
При больших механических напряжениях величина расщепления, создаваемого деформацией, может стать больше величины ![]() (для кремния
(для кремния ![]() =0,04эВ) и может приводить к неполному насыщению пьезосопротивления.
=0,04эВ) и может приводить к неполному насыщению пьезосопротивления.
Список литературы:
1. Brown D. M., Bray R., Analysis of Lattice and Ionized Impurity Scattering in p-Type Germanium //Phys. Rev. — 1962. — V. 127. — P. 1593.
2. Glicksman Maurice. Magnetoresistance of Germanium—Silicon Alloys. // Phys. Rev. — 1955. —V. 100. — P. 1146.
3. Gold L. and Roth L. M. Galvanomagnetic Theory for Electrons in Germanium and Silicon: Magnetoresistance in the High—Field Saturation Limit. // Phys. Rev. — 1956. — V. 103. — P. 61.
4. Lawaetz P. Low-Field Mobility and Galvanomagnetic Properties of Holes in Germanium with Phonon Scattering.// Phys. Rev. — 1968. — V.174. — P. 867.
5. Lax B., Mavroides I. G. Statistics and Galvanomagnetic Effect in Germanium and Silicon with Warped Energy Surfaces // Phys. Rev. — 1955. — V. 100. № 7 — Р. 1650—1657.
6. Mavroides I. G., Lax B. Magnetoresistance of Holes in Germanium and Silicon with Warped Energy Surfaces. //Phys. Rev. — 1957. — V. 107. — P. 1530.
7. Mavroides I. G., Lax B. Magnetoresistance of Holes in Germanium and Silicon with Warped Energy Surfaces. //Phys. Proc. Rev. — 1957. — V. 108. — P. 1648.
8. McClure J. W., //Field Dependence of Magnetoconductivity. //Phys. Rev. — 1956. — V. 101. — P. 1642.
9. Pearson G. L., Suhl H. The Magneto—Resistance Effect in Oriented Single Crystals of Germanium. //Phys. Rev. — 1951. — V. 83. — P. 768.
дипломов

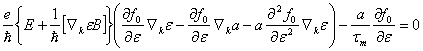 .
. ,
,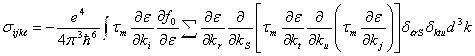 .
.
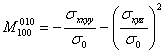 ;…;
;…;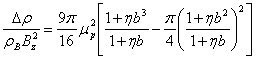 ,
,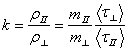 ,
, ,
, 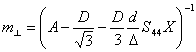 Х║[111].
Х║[111].
Оставить комментарий