Трехмерная модель адсорбционно-диффузионных процессов с тремя состояниями

Алексей Александрович Астапков

аспирант, ЯрГУ им. П. Г. Демидова, г. Ярославль

Е-mail: ph4ntom@mail.ru

Николай Алексеевич Рудь

канд. физ.-мат. наук, доцент ЯрГУ им. П. Г. Демидова, г .Ярославль

Павел Геннадьевич Морозов

аспирант, Московская авиационная академия, г. Москва

Структуры с пониженной размерностью проявляют ряд необычных свойств, что связанно с особенностями перераспределения энергии в этих структурах. В работе [5] отражено влияние адсорбционных процессов на токопрохождение в пористом кремнии, в частности было обнаружено периодическое изменение динамических характеристик с изменением времени. Адсорбция и десорбция молекул (атомов), способных изменять свое зарядовое состояние, проявляет периодичность развития динамики процесса во времени, подобные автоколебательные эффекты обнаружены при полевой десорбции калия с поверхности, на которой находится смесь адсорбатов калий – золото [1, 2]. Совокупность экспериментальных данных, полученных в различных экспериментах, свидетельствуют о необходимости развития теоретической базы, способной качественно и количественно описать и объяснить их. В реальных экспериментах помимо адсорбционных процессов, проходящих на поверхности твердого тела, в объеме происходят реакционно-диффузионные процессы, для их описания необходима трехмерная модель, которая смогла бы учесть как адсорбционные процессы, происходящие на поверхности, так и реакционно-диффузионные процессы, проходящие в приповерхностных слоях. Однако экспериментов, которые смогли бы качественно показать динамические процессы, проходящие в приповерхностных слоях, на данный момент не существует. Отсутствие экспериментальных данных создает сложности в построении трехмерной модели адсорбционно-диффузионных процессов. По этой причине в ходе моделирования за основу используются экспериментальные данные, полученные на поверхности твердого тела.

Динамические процессы в активных средах (реакционно-диффузионные процессы в физике, химии) традиционно представляются дифференциальными уравнениями (или системами уравнений) с частными производными вида:

,

где D – коэффициент диффузии, U – функция распределения, F(U) – дифференцируемая нелинейная функция. Из-за нелинейности реакционной части F(U) аналитические решения получить крайне сложно, задача усложняется, при переходе к большему количеству частиц, а при переходе к трехмерному пространству задача становится, практически, не решаема. Численные методы решения либо плохо распараллеливаются, т. е. имеют неявные схемы решений, либо ограничены условиями устойчивости и точности. В свою очередь алгоритмы КА-диффузии подобных ограничений не имеют. Это означает, что подобные задачи можно решать с помощью дискретной модели асинхронного клеточного автомата, рассматривая этот подход как альтернативу классическому описанию динамических процессов. Реакционно-диффузионные процессы есть комбинация диффузионных и реакционных процессов, о которых будет сказано ниже.

Представим моделируемый объем в виде набора монослоев. Каждый монослой представляет собой самостоятельное клеточное множество. Подвергнем клеточное множество разбиению на блоки 2х2х2 двумя различными способами, которые будем называть четным и нечетным. Четное разбиение – это разбиение, в котором элементарные ячейки на главной диагонали блоков имеют четную сумму координат; нечетное – это разбиение, в котором элементарные ячейки на главной диагонали блоков имеют нечетную сумму координат. Каждый из получившихся блоков может совершить поворот вдоль одной из координатных осей на 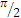. В случае поставленной задачи оператор перехода Θ меняет состояния клеток между собой, разворачивая блоки против или по часовой стрелке вокруг случайной координатной оси. В общем случае на каждой итерации, в каждом блоке, выполняется следующее отображение:

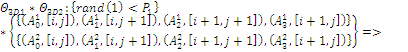
где rand(1) – случайное число (0,1), [i, j] – имя элементарной ячейки, Р – вероятность, «» – объединение конфигураций.

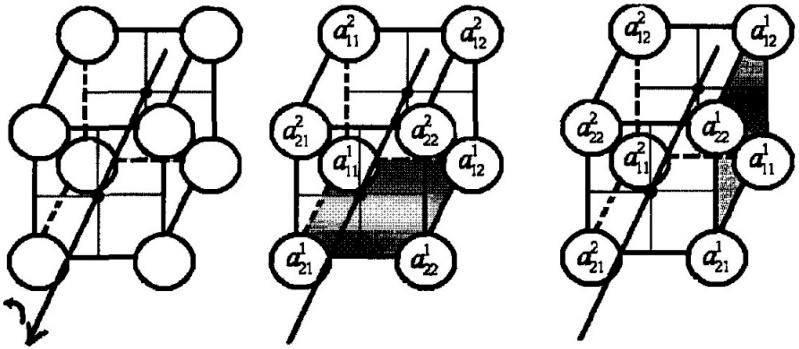
Рисунок 1. Поворот на 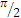 по часовой стрелке вокруг координатной оси «х».

На рис. 1 более наглядно представлен поворот на 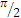 по часовой стрелке вокруг оси «х».

Представим структуру твердого тела в виде простой кубической сингонии. Связанные с моделью поверхность и объем твердого тела считаются идеальными, это означает, что не учитываются дефекты и неоднородности, отсутствуют дислокации и вакансии. Каждая частица является элементарной ячейкой клеточного автомата (КА) и имеет определенный цвет. Белая клетка – молекула исходного вещества, базы, без адсорбированной молекулы; серая клетка – это молекула исходного вещества, базы, с нейтральной адсорбированной молекулой; черная клетка – молекула исходного вещества с заряженной адсорбированной молекулой. Схема перезарядки состояния элементарной ячейки изображена на рис. 2.

Конечное состояние элементарной ячейки зависит от времен жизни, которое определяет через сколько тактов (итераций) клеточного автомата произойдет перезарядка; вероятности перехода из одного состояния в другое. Так же конечное состояние элементарной ячейки зависит от окружения – 26-ти связной окрестности. Каждая соседняя клетка находится в одном из трех состояний, в зависимости от этого происходит переход.

Рисунок 2. Схема перезарядки состояний.

A_k(t) – состояние k-ого элемента системы в момент времени (t).

A_k(t+1) – состояние k-ого элемента системы в момент времени (t+1).

Каждая элементарная ячейка принимает, как было сказано выше, следующие значения:

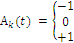, соответственно .

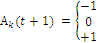Состояние, которому присваивается значение «-1» соответствует «белой» элементарной ячейке, «0» соответствует «серой» элементарной ячейке, «+1» соответствует «черной» элементарной ячейке.

Реализация вышеописанного алгоритма позволяет смоделировать обе части уравнений реакционно-диффузионного типа. Обе части алгоритма не разделены, но работают они независимо друг от друга.

Представим параллелепипед со структурой простой кубической сингонии размером 200х200х50 элементарных ячеек, таким образом, обрабатывалось 2х10⁶ частиц. Адсорбция на поверхность объекта производилась из бесконечного источника, перпендикулярно плоскости «XY». Коэффициент диффузии D изотропный и равный единице. Алгоритм модели произвёл 500 итераций. Заданные времена жизни для элементарных ячеек: для «белой элементарной ячейки» – 10 итераций, для «серой элементарной ячейки» – 5 итераций, для «черной элементарной ячейки» – 5 итераций. Все переходы равновероятны. Условия, для осуществления переходов для «серой элементарной ячейки» и «черной элементарной ячейки» по 4 и 5 соседей соответствующего цвета. На рис. 3 представлен ряд мгновенных снимков сечений в плоскости «ХУ», отражающих эволюцию системы в различные моменты времени при реализации описанного выше алгоритма. Рис. 3а соответствует поверхностному слою, рис. 3б соответствует приповерхностному слою №1, рис. 3в соответствует приповерхностному слою №4. На 50 итерации клеточного автомата начинают активно работать несколько ведущих центров, к 100 итерации эти ведущие центры начинают взаимодействовать друг с другом. В результате конкуренции к 200 итерации большая часть ведущих центров либо вырождается, либо поглощается, что приводит к тому, что к 300 итерации из множества ведущих центров остается только один.

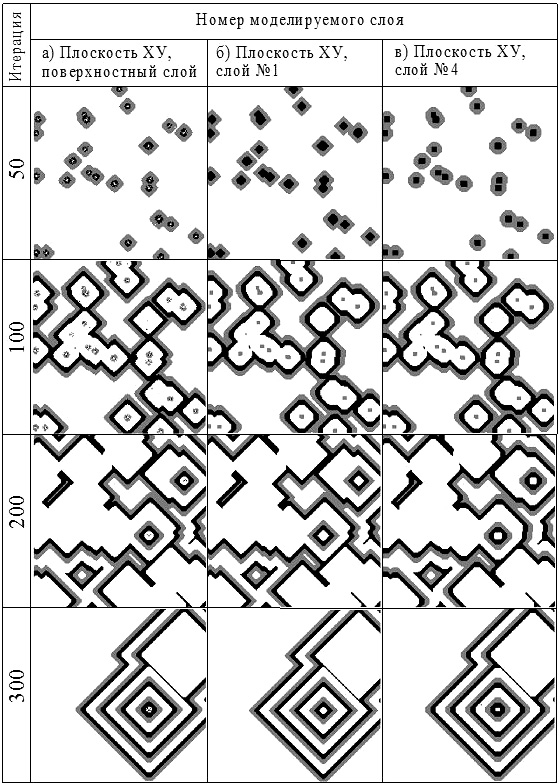
Рисунок 3. Эволюция системы, плоскость ХУ.

Образовавшиеся ведущие центры в ходе эволюции системы могут вырождаться, быть поглощенными одним из ведущих центров, или продолжать взаимодействие по средствам солитонных волн, в дальнейшем и эти ведущие центры вырождаются и система приходит в начальное состояние, это вырождение является следствием конкуренции нескольких ведущих центров. Подобные мгновенные снимки поверхностных слоев представлены в работах [3, 4], однако они отражают лишь состояние поверхности. Предлагаемая нами модель КА позволяет проводить анализ любого слоя, выбрав необходимую плоскость сечения во взаимно ортогональных направлениях.

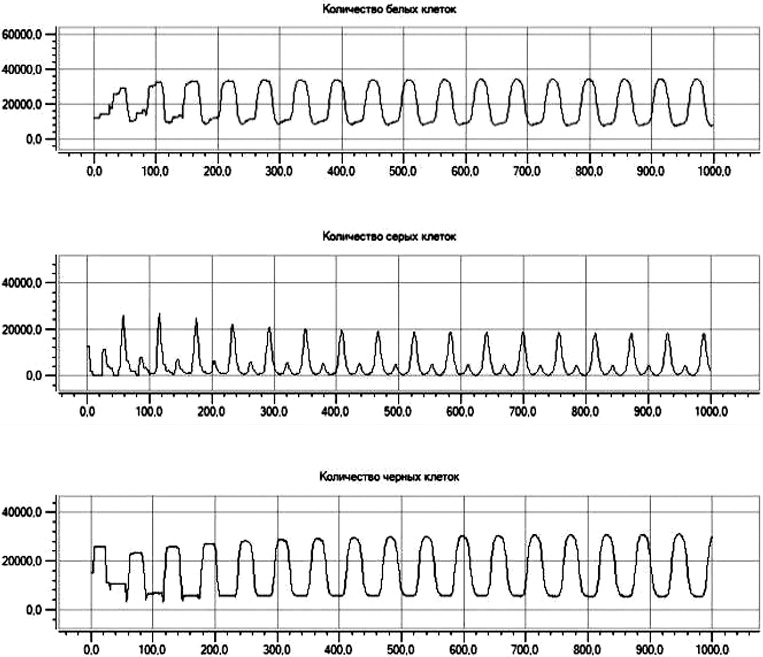
Рисунок 4. Зависимости числа клеток различных цветов от времени для слоя №4.

Выбирая необходимый слой, можно наблюдать за качественной и количественной картиной динамических процессов. Так на рис. 4 представленны зависимости числа клеток различных цветов от времени для четвертого слоя. Подобные измерения невозможно снять в реальном экспиременте, но наша модель КА позволяет производить замеры по любому монослою в любой из трех ортогональных плосткостях. Пересчет зависимостей по всему объему позволяет произвести сравнения с эксперементальными данными. Переход из одного состояния в другое определяется временем жизни ячейки, вероятностью перехода из одного состояния в другое и соседями, находящимися в определенном состоянии, достаточном для осуществления перехода. Применение подобной модели позволяет наблюдать динамические процессы как на поверхности, так и в приповерхностных слоях.

Реализация описанного выше достаточно простого алгоритма приводит к большому числу разнообразных динамических режимов. Таким образом, при переходе от хаоса к синхронизации система проходит стадию локальной синхронизации ведущих центров. Это означает, что возникают ведущие центры с определенными частотами колебаний, и дальнейшее развитие системы является результатом конкуренции этих ведущих центров с последующим поглощением, вырождением или переходом в режим испускания автоволн. Несмотря на простоту алгоритма, он очень требователен к вычислительным мощностям, что вызывает массу трудностей в реализации и накладывает искусственные ограничения.

Список литературы:

1.            Бернацкий Д. П., Павлов В. Г. Автоколебательные эффекты при полевой десорбции щелочных металлов // Письма в ЖТФ. — 2000. — Т. 26, № 6. — С. 22-26.

2.            Бернацкий Д. П., Павлов В. Г. Полевая десорбция пленки калий-золото на вольфраме // ФТТ. — 2004. — Т. 46, № 8. — С. 1494-1497.

3.            Каплий С. А., Проказников А. В., Рудь Н. А. Дискретная модель адсорбции с конечным числом состояний // ЖТФ. — 2005.— Т. 75, № 12. — С. 1-9.

4.            Каплий С. А., Проказников А. В., Рудь Н. А. Дискретная модель адсорбции с тремя состояниями //Письма в ЖТФ. — 2004. — Т. 30, № 14. —С. 46-52.

5.            Лаптев А. Н., Проказников А. В., Рудь Н. А. Автоколебательные процессы в сенсорных структурах на основе низкоразмерных систем // Микросистемная техника. — 2002. — № 6. — С. 31-40.