Статья опубликована в рамках: III Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 27 декабря 2011 г.)
Наука: Физика
Секция: Оптика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ ВОЛНОВОДНЫХ СТРУКТУР МЕТОДОМ РАСПРОСТРАНЕНИЯ ЛУЧА FFT-BPM
Андросик Андрей Борисович
канд. техн. наук, доцент, Государственный открытый Университет, г. Москва
Воробьев Сергей Андреевич
канд. техн. наук, доцент, Государственный открытый Университет, г. Москва
Мировицкая Светлана Дмитриевна
канд. техн. наук, доцент, Государственный открытый Университет, г. Москва
E-mail:vorsa_57@mail.ru
Одним из фундаментальных аспектов интегральной оптики является анализ и имитация распространения электромагнитной волны в приборах фотоники, основанных на волноводных структурах, включая оптические волноводы. В работе рассматривается метод распространения луча (BPM), который используется для анализа неоднородных волноводных структур.
Решение уравнения Гельмгольца или уравнения Френеля для оптического распространения излучения в волноводах, известно как метод распространения луча (BPM). Для решения уравнения Френеля были предложены два численных алгоритма. В одном из них, оптическое распространение моделируется как спектр плоской волны в пространственной частотной области, а влияние неоднородности среды интерпретируется как изменение фазы на каждом шаге пространственного распространения. Если в пространственной и спектральной областях применяется быстрое преобразование Фурье (БПФ), то метод называется BPM с быстрым преобразованием Фурье (БПФ BPM - FFT-BPM) [1, с. 96].
Распространение ЭМ волн в неоднородных средах можно непосредственно описать в пространственной области с помощью конечно - разностной схемы (FD). Этот метод позволяет выполнять имитационное моделирование сильно направляющих структур, а также структур, изменяющихся в направлении распространения. Метод распространения луча, позволяющий получить решение параксиальной формы скалярного волнового уравнения в неоднородной среде, используя метод конечных разностей, называется FD-BPM. Методы, дающие решение векторного волнового уравнения и основанные на конечных разностях, называются FD-VPBM. Известно промежуточное приближение, которое начинается с волнового уравнения, но не учитывает условие связи между поперечными составляющими полей; такой подход называется полувекторный (semi-vectorial) (FD-SVBPM) метод [3, с. 466]. В данной работе рассмотрен метод FFT-BPM, удобный для решения задачи моделирования волноводной структуры.
Скалярное уравнение Гемгольца имеет вид
|
|
(1) |
где Ñ2 – лапласиан
|
|
(2) |
а k0 – волновое число в вакууме.
Для функции y(x,y,z), распространяющейся в направлении оси +z, можно воспользоваться приближением плавного изменения (slowly varying envelope approximation – SVEA). При этом функцию y(x,y,z) можно представить виде двух сомножителей: плавно меняющейся функции f(x,y,z) и быстро осциллирующего фазового члена exp(-j×b×z)
|
|
|
Здесь
|
|
(4) |
где neff – эффективный показатель преломления, связанный с показателем преломления сердцевины и оболочки.
Вторую производную волновой функции y(x,y,z) по z можно представить как
|
|
(5) |
в (1) и, разделив левую и правую часть на exp(-j×b×z), можно записать
|
|
(6) |
где Ñ^2 – лапласиан в поперечном направлении, который имеет вид
|
|
(7) |
Использование соотношения
|
|
(8) |
приводит к
|
|
(9) |
В последнем выражении учитывается вторая производная волновой функции f(x,y,z) по z, поэтому уравнение (9) является широкоугольной формулировкой. С другой стороны, если
|
|
(10) |
для уравнения (9) получается
|
|
(11) |
Допущение, которое не учитывает вторую производную волновой функции f(x,y,z) по z, называется приближением Френеля или параксиальным приближением. Волновая функция f(x,y,z) имеет вид
|
|
(12) |
А волновую функцию f(x,y,z+Dz), которая отличается от функции f(x,y,z) на величину Dz в направлении распространения, можно записать как
|
|
(13) |
Целесообразно использовать соотношение
|
|
|
и допущение, что Dn – достаточно малая величина, чтобы не учитывать (Dn)2.
После преобразований можно записать
|
|
|
Уравнение (14) позволяет получить результат с ошибкой порядка (Dz)3. Это означает, что шаг приращения по направлению распространения Dz в методе FFT-BPM должен быть достаточно малым.
Ниже рассмотрен физический смысл каждого из элементов уравнения (14). Если допустить, что показатель преломления однороден в области анализа, тогда c будет равно нулю. В этом случае, уравнение (14) принимает вид
|
|
(15) |
Это означает, что оператор
|
|
(16) |
соответствует распространению волновой функции на расстояние Dz в свободном пространстве. Поэтому, первый и третий члены уравнения (14) соответствуют распространению света в свободном пространстве на расстояние Dz/2. Таким образом, уравнение (14) показывает, что волновую функцию в плоскости z+Dz можно получить, сначала перемещая волновую функцию в свободном пространстве на Dz/2, затем задавая фазовый сдвиг (-c), связанный с фазовым сдвигом линз и, в заключении, смещая волновую функции в свободном пространстве на Dz/2.
Далее получено выражение для оператора распространения свободного пространства (16), и оно применено к волновой функции.
Дискретное преобразование Фурье (т. е. представление волновой функции в спектральной области) имеет вид
|
|
(17) |
где
|
|
|
|
|
(18) |
|
|
|
|||
|
|
|
|||
Здесь, X и Y – шаг по оси x и y, соответственно. Обратное дискретное преобразование Фурье имеет вид
|
|
(19) |
При использовании оператора (16) и приведенных выше рассуждений, волновая функция на расстоянии z+Dz/2 принимает вид
|
|
(20) |
Волновая функция в плоскости z+Dz/2 получена, заменяя z на z+Dz/2 в уравнении (19)
|
|
(21) |
С другой стороны, подстановка (19) в (20), приводит к:
|
|
(22) |
После преобразований получается другое выражение для волновой функции в плоскости z+Dz/2
|
|
(23) |
Поскольку волновые функции f(x,y,z+Dz/2), задаваемые уравнениями (21) и (23) равны, можно записать следующее соотношение:
|
|
(24) |
Уравнение (24) показывает соотношение между спектральной волновой функцией ![]() в плоскости z+Dz/2 и плоскости z. Фазовый член уравнения (24)
в плоскости z+Dz/2 и плоскости z. Фазовый член уравнения (24)
|
|
|
учитывает факт распространения на расстояние Dz/2 в свободном пространстве. Уравнение (23) является обратным дискретным преобразованием Фурье функции
|
|
|
Таким образом, получается, что оператор
|
|
(25) |
соответствует применению математической операции
|
|
(26) |
к пространственной функции f(x,y,z). Здесь символы F и F-1 соответствуют прямому и обратному дискретному преобразованию Фурье. Переменные kx и ky можно записать как
|
|
|
|
(27) |
Таким образом, процедура расчета методом FFT-BPM включает несколько шагов [2, с. 175, 4, с. 1275]:
1. Вычисляется Фурье-образ волновой функции f(x,y,z), используя прямое дискретное преобразование Фурье.
2. Формируется Фурье-образ волновой функции, смещенный на расстояние Dz/2 путем умножения на коэффициент
|
|
|
Это умножение соответствует смещению на Dz/2 в свободном пространстве.
3. Используется обратное преобразование Фурье и определяется пространственная функция перед фазосдвигающей линзой. Путем умножения волновой функции на фазовый сдвиг, получается волновая функция после фазосдвигающей линзы
|
|
|
|
Берется прямое преобразование Фурье по отношению к волновой функции и умножается на коэффициент
|
|
|
что соответствует смещению на Dz/2 в свободном пространстве; получается Фурье-спектр волновой функции в плоскости Dz.
4. Используется обратное преобразование Фурье и вычисляется пространственная волновая функция в плоскости Dz.
В случае, когда нет необходимости получать пространственную волновую функцию при каждом смещении z+Dz, можно перейти от шага 2 к шагу 4 и повторить шаги 2-4.
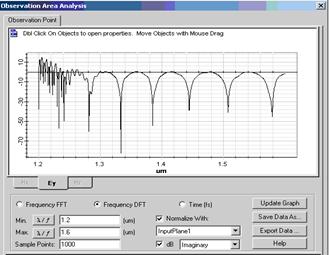
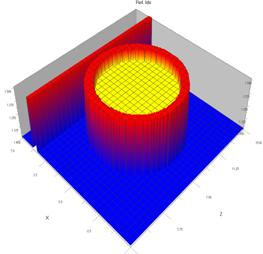
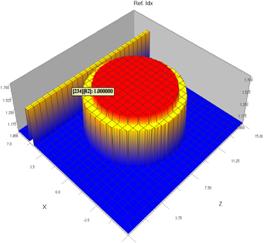
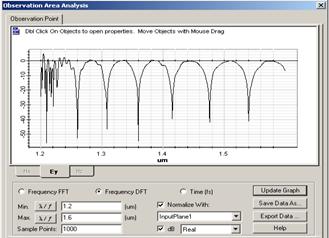
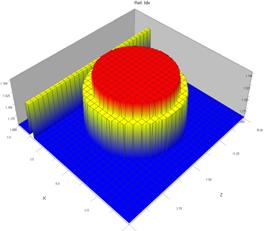
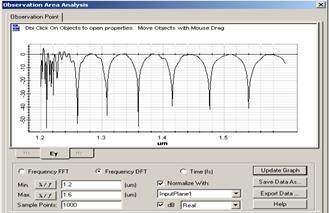
Результаты модельных исследований для структуры, состоящей из волновода и кольца, представлены на рис. 1. Исследования проводились для четырех типов резонаторных структур с одинаковыми геометрическими характеристиками и разными показателями преломления.
Рисунок 1. Результаты расчетов резонансных структур
|
|
Дискретное преобразование Фурье спектра в функции длины волны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретное Фурье преобразование спектра имеет периодический характер. В каждой из картин наблюдается один ярко выраженный пик (для первого варианта при l=1,27 мкм, для второго - l=1,541 мкм, для третьего l=1,418 мкм, для четвертогоl=1,36 мкм). Для случаев (б-г) можно заметить смещение пика в сторону начала координат, амплитуда пика пропорционально уменьшается по абсолютной величине.
Список литературы:
1. Андросик А. Б., Воробьев С. А., Мировицкая С. Д. Волноводная и интегральная фотоника.- М.: МГОУ, 2011, 370 стр.
2. Андросик А. Б., Воробьев С. А., Мировицкая С. Д. Моделирование фотонных структур методом конечных разностей во временной области.- Наука и современность-2011, Новосибирск, часть 2, с. 175-187.
3. Hadley G.R., Smith R. E. Full-vector waveguide modeling using an iterative finite-difference method with transparent boundary conditions //J. Lighhtwave Techn., 1995. V. 13. N. 3. P. 465-469.
4. Masoudi H. M., Al-Sunaidi M.and M.Arnold J. Time-domain finite-difference beam propagation method, IEEE Photonics Technology Letters, vol.11, pp. 1274–1276, Oct. 1999.
дипломов
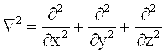 ,
,
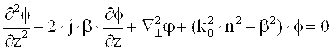 ,
, .
. .
.
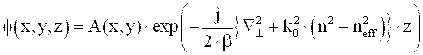 .
. .
.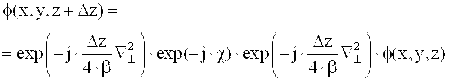 .
.

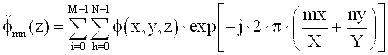 ,
,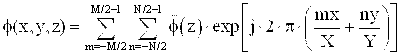 ,
, .
. .
.

 .
.




 .
.

Оставить комментарий