ОСОБЕННОСТИ ИНТЕРФЕРЕНЦИИ ВОЛН В НЕВЗАИМНЫХ СРЕДАХ

Глущенко Александр Григорьевич

д-р физ.-мат. наук, профессор, Поволжский государственный университет телекоммуникаций и информатики (ПГУТИ), г. Самара

Глущенко Евгения Павловна

канд. физ.-мат. наук, Поволжский государственный университет телекоммуникаций и информатики (ПГУТИ), г. Самара

Иванов Виктор Васильевич,

д-р техн. наук, профессор, Поволжский государственный

университет сервиса, г. Тольятти,

Устинова Елена Сергеевна,

старший преподаватель кафедры информационного и электронного сервиса Поволжский государственный университет сервиса, г. Тольятти,

e-mail: zep646@yandex.ru 

При наложении когерентных волн, движущихся во взаимно противоположных направлениях, формируются стоячие волны, которые позволяют накапливать энергию колебательных процессов. В литературе описываются физические свойства стоячих волн в однородных, изотропных средах, резонаторах на основе волноводных структур [1-3]. Стоячие волны в невзаимных структурах и средах не рассматривались. Вместе с тем, анализ показывает, что невзаимность параметров существенно меняет физические свойства стоячих волн. Установлено, что колебательный процесс стоячей волны за счет невзаимных свойств сред носит характер биений. Колебания пространственно разнесенных точек стоячей волны теряют свойство синфазности.

Рассмотрим здесь особенности звуковых стоячих волн в упругой среде, обладающей невзаимными свойствами. На рис. 1 показана модель резонатора в виде экранированной в плоскостях x=0, d среды. Фазовая скорость распространения волн (в неподвижной среде). Если резонатор привести в движение вдоль координатной оси 0x со скоростью u , он приобретает свойства невзаимной среды для прямых () и обратных () упругих волн.

Рисунок 1. Наложение прямой (k₁) и отраженной (k₂) волн в невзаимной среде (d – длина, u – скорость движения среды).

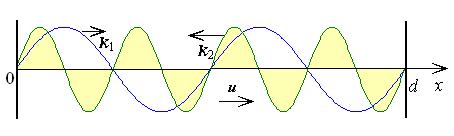
Скорость среды здесь играет роль параметра невзаимности, и при u=0 структура обладает взаимными свойствами. Помимо скоростей различаются волновые числа и длины прямой и обратной волн:

, , , .

Для прямой и отраженной волн сохраняется временная когерентность волн, но физические свойства стоячей волны изменяются и описываются обобщенным уравнением:

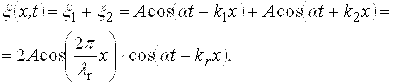                        (1)

где длина стоячей волны , волновое число  и скорость  результирующего волнового процесса определяются соотношениями:

, ,  .

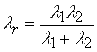Обычно, без каких-либо оговорок, принимается, что равны и волновые числа прямой и обратной волн (). Однако это справедливо только в частном (хотя и наиболее распространенном) случае сред и структур, обладающих взаимными свойствами (одинаковыми параметрами, в частности, одинаковой скоростью распространения прямых и обратных волн ). Уравнение (1) описывает квазистоячую волну - результирующий волновой процесс, который при устранении невзаимности переходит в обычную стоячую волну. Первый сомножитель уравнения обобщенной стоячей волны - амплитуда, которая зависит от координаты и от скоростей прямых и обратных волн. Второй сомножитель показывает (в отличие от обычных стоячих волн) наличие волнового процесса с фазовой скоростью . Направление распространения результирующего волнового процесса зависит от соотношения скоростей  и : 1) совпадает с ось 0x при скоростях, удовлетворяющих соотношениям:  или ; 2) направление распространения противоположно оси 0x при скоростях, удовлетворяющих соотношениям:  или . Таким образом, при малых скоростях перемещения среды  направление волнового процесса противоположно направлению движения этой среды. В отсутствие движения () среда проявляет свойства взаимности  и уравнение (1) сводится к известному уравнению стоячей волны.

В выражении для фазы уравнения стоячей волны во взаимной среде не входит координата и колебательные процессы во всех точках расположенных между ближайшими узлами в областях синфазны по отношению друг к другу. Напротив, из уравнения (1) следует, что в невзаимных средах синфазны только колебания в точках, для которых выполняется соотношение:

.

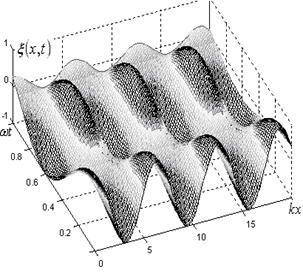
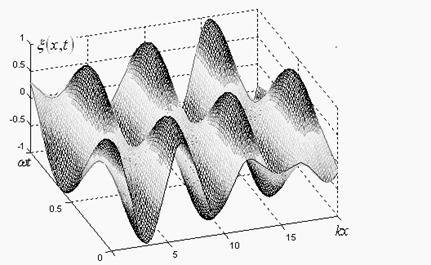
Характер волнового процесса в результате наложения прямых и обратных волн в средах со взаимными свойствами (а) и в невзаимных средах (b) в зависимости от координаты и времени показан на рис. 2. Невзаимность свойств среды приводит к возникновению пространственных биений.

В точках (узлы), координаты которых удовлетворяют условию:

,

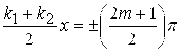m=0,1,2,…, суммарная амплитуда колебаний равна нулю. Координаты узлов определяются соотношениями:

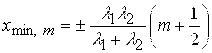.                                        (2)

В точках, где координаты удовлетворяют условию:

суммарная амплитуда достигает максимальных значений 2A. С течением времени (в отличие от стоячих волн во взаимных средах), амплитуда колебаний во всех точках (кроме узлов) меняется по периодическому закону (рис. 2, b). Координаты пульсирующих пучностей определяются из соотношения:

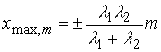.                                                  (3)

Рисунок 2. Характер интерференции прямых и обратных волн во взаимных (a - стоячая волна) и невзаимных (b) средах

Резонансные частоты резонатора с размером :

 .

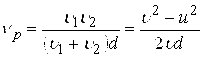При росте скорости среды вплоть до скорости распространения волн () резонансная частота , волновой процесс отсутствует (рис. 3).

Рисунок 3. Зависимость резонансной частоты от скорости стержня (,)

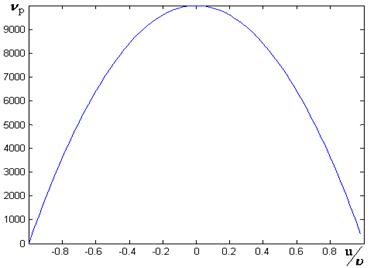
Выводы. Интерференция прямых и обратных когерентных волн в невзаимных средах имеет свои особенности. Стоячие волны становятся нестационарными - на распределение поля стоячей волны накладывается волновой процесс, направление которого определяется параметром невзаимности. Колебания соседних точек теряют свойство синфазности. Резонансные частоты зависят от параметра невзаимности среды. Таким образом, введение в резонаторы сред с невзаимными параметрами существенно расширяет возможности резонансных структур в управлении их параметрами и представляет практический интерес.

Список литературы

1.Горелик Г. С. Колебания и волны. М.: Физматлит, 2008. 656 с.

2. Глущенко А. Г., Захарченко Е. П. Стимулированная прозрачность запредельных структур с активными средами. LAP LAMBERT Academic Publishing, 2011. 186 с.

3. Дубнищев Ю. Н. Колебания и волны. СПб.: Лань, 2011. 384 с.