Статья опубликована в рамках: II Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 30 ноября 2011 г.)
Наука: Физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
ИССЛЕДОВАНИЕ РАЗЛИЧНЫХ ВИДОВ СИЛ ТРЕНИЯ, ВОЗНИКАЮЩИХ ПРИ ДВИЖЕНИИ ПОРШНЯ В ТРУБЕ
Насибуллаев Ильдар Шамилевич
к. ф.-м. н., ФГБОУ УГАТУ, г. Уфа
Насибуллаева Эльвира Шамилевна
доцент, к. ф.-м. н., Институт Механики УНЦ РАН, г. Уфа
E-mail: elvira98@mail.ru
Работа выполнена при финансовой поддержке РФФИ (проекты № 11-01-97007, 11-08-00823, 11-08-97046).
Введение. Исследование влияния трения между внутренними частями технических элементов на характер движения элементов (например, движение поршня в трубе) является актуальной задачей, так как позволяет определить параметры, при которых трение будет минимальным, а коэффициент полезного действия — максимальным.
С точки зрения трибологии различают различные виды трения, прежде всего сухое и вязкое трение. В первом приближении коэффициент сухого трения λ является коэффициентом пропорциональности между силой трения Ff и силой нормальной реакции Nn (закон Амонтона–Кулона). Сила вязкого трения проявляется при движении твердого тела по поверхности жидкости и определяется напряжением, создаваемым жидкостью на поверхности твердого тела. Величина силы вязкого трения Fv ньютоновской жидкости пропорциональна площади контакта и градиенту скорости в направлении, перпендикулярном движению (закон Ньютона). Коэффициентом пропорциональности является величина динамической вязкости жидкости μ [2].
Таким образом, для определения силы вязкого трения, действующей на твердую поверхность, необходимо решить гидродинамическую задачу движения жидкости.
Математическая модель. Рассмотрим движение поршня радиуса r1 и массой m внутри цилиндра радиуса 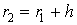 (здесь h — зазор между поршнем и цилиндром), заполненного жидкостью с плотностью ρ и динамической вязкостью μ, под действием периодического по времени перепада давления
(здесь h — зазор между поршнем и цилиндром), заполненного жидкостью с плотностью ρ и динамической вязкостью μ, под действием периодического по времени перепада давления 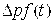 с
с 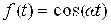 (см. рис. 1), где
(см. рис. 1), где 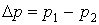 — амплитуда давления;
— амплитуда давления;  — угловая частота; f — частота осцилляций давления. Начало цилиндрической системы координат поместим на оси в центре цилиндра. Координаты в радиальном и осевом направлениях обозначим через r и z соответственно, а соответствующие компоненты скорости течения жидкости — через vr и vz. Скорость движения поршня имеет только одну компоненту vp вдоль оси z.
— угловая частота; f — частота осцилляций давления. Начало цилиндрической системы координат поместим на оси в центре цилиндра. Координаты в радиальном и осевом направлениях обозначим через r и z соответственно, а соответствующие компоненты скорости течения жидкости — через vr и vz. Скорость движения поршня имеет только одну компоненту vp вдоль оси z.
|
|
|
Рисунок 1. Схема геометрии задачи |
Уравнение движения поршня описывается вторым законом Ньютона:
 ,
, 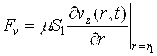 (1)
(1)
где Sp — площадь поперечного сечения поршня; 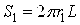 — площадь внешней поверхности поршня; L — длина поршня. Второе слагаемое уравнения (1) описывает силу вязкого трения Fv. В начальный момент времени поршень покоится, т.е.
— площадь внешней поверхности поршня; L — длина поршня. Второе слагаемое уравнения (1) описывает силу вязкого трения Fv. В начальный момент времени поршень покоится, т.е. 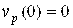 .
.
Пренебрегая краевыми эффектами, которые возникают вблизи краев поршня, и для случая осесимметричного течения получим уравнение движения жидкости [1]:
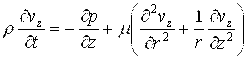 ,
,  . (2)
. (2)
Граничные условия на поверхности поршня и цилиндра определяются из условия залипания: 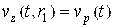 ,
,  .
.
Результаты. Уравнения (1)–(2) с граничными условиями записывались в виде конечно-разностной схемы и решались численно методом Ньютона–Рафсона. При разбиении сетки по координате на 50 узлов и 2·105шагов за 1 с по времени погрешность вычислений не превышала 1%. Расчеты проводились при следующих значениях параметров: 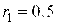 см,
см, 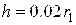 ,
, 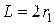 ,
, 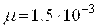 Па·с,
Па·с,  кг/м3,
кг/м3, 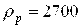 кг/м3,
кг/м3, 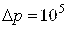 Па,
Па,  Гц.
Гц.
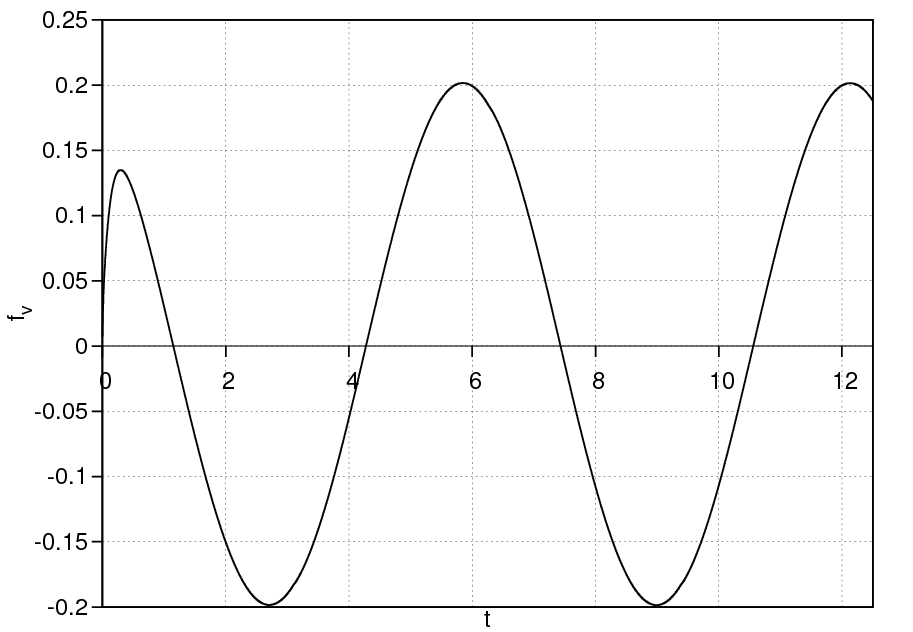
Рисунок 2. Зависимость силы воздействия жидкости fv на поршень
На рис. 2 показана зависимость силы 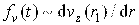 , действующей на поршень со стороны жидкости. При совпадении знаков fv и скорости поршня vp эта сила ускоряет движение поршня, т.е. поршень увлекается потоком жидкости, а при различных знаках fv проявляется как сила вязкого трения, т.е. уменьшает скорость поршня). Двоякая роль силы fv объясняется тем, что на жидкость, как и на поршень, действует одинаковый градиент давления и, в силу того, что инерция поршня выше, жидкость движется быстрее поршня и увлекает его за собой. В моменты, когда градиент давления меняет знак, поршень продолжает двигаться по инерции, а течение жидкости меняет свое направление и fv действует как сила вязкого трения.
, действующей на поршень со стороны жидкости. При совпадении знаков fv и скорости поршня vp эта сила ускоряет движение поршня, т.е. поршень увлекается потоком жидкости, а при различных знаках fv проявляется как сила вязкого трения, т.е. уменьшает скорость поршня). Двоякая роль силы fv объясняется тем, что на жидкость, как и на поршень, действует одинаковый градиент давления и, в силу того, что инерция поршня выше, жидкость движется быстрее поршня и увлекает его за собой. В моменты, когда градиент давления меняет знак, поршень продолжает двигаться по инерции, а течение жидкости меняет свое направление и fv действует как сила вязкого трения.
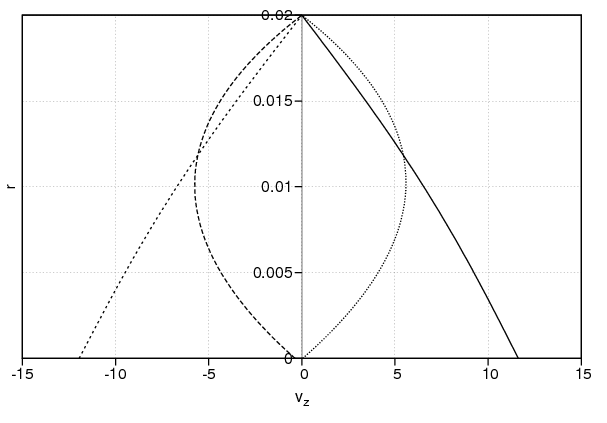
Рисунок 3. Профили скорости жидкости 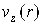 в различные моменты времени: 0.25 периода (—); 0.5 периода (– –); 0.75 периода (- -); 1 период (···)
в различные моменты времени: 0.25 периода (—); 0.5 периода (– –); 0.75 периода (- -); 1 период (···)
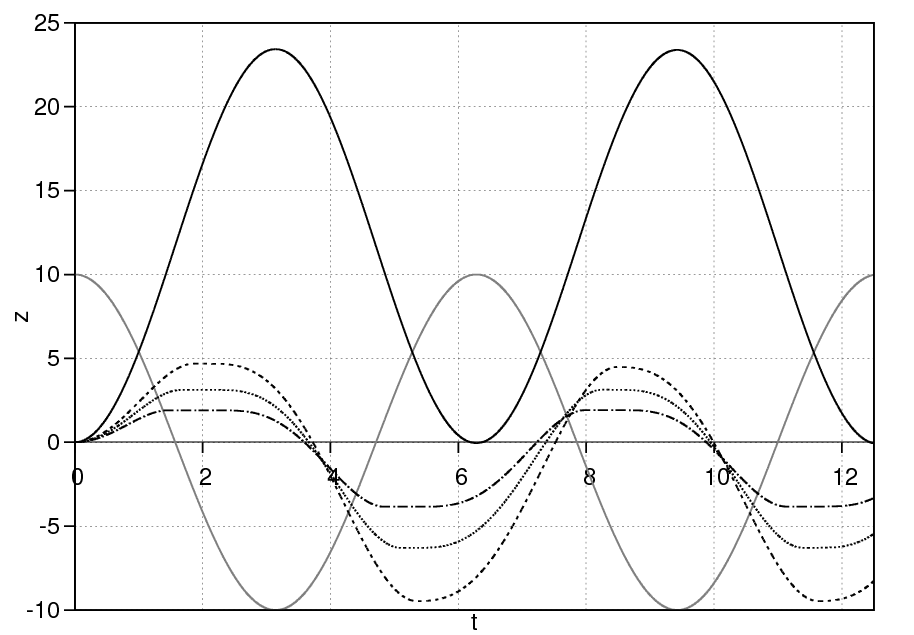
Рис. 4. Координаты положения поршня z от времени t (черные линии): без трения (—); 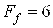 Н (– –);
Н (– –);  Н (- -);
Н (- -); 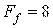 Н (···). Серая линия — давление от времени
Н (···). Серая линия — давление от времени
Отметим, что если убрать действие перепада давления на жидкость (т.е. убрать пуазейлевскую составляющую и оставить только сдвиговую), то fv будет действовать как сила вязкого трения в любой момент времени. Это хорошо видно на рис. 3, где показаны профили скорости жидкости vz в различные моменты времени. Видно, что при малых скоростях движения поршня (0.5 и 1 период) vp профили скорости жидкости vz соответствуют пуазейлевскому течению, а при больших скоростях vp (0.25 и 0.75 периода) реализуется сдвиговое течение. Сила fv по величине намного меньше силы, действующей на поршень со стороны градиента давления, поэтому характер движения поршня с силой вязкого трения и без трения слабо различаются (отличия ~ 2%).
Рассмотрим поведение системы при  , т.е. когда зазор между поршнем и трубой отсутствует и на поршень действует сила сухого трения. Если действующая на поршень сдвигающая сила F1 мала, то поршень покоится из-за действия силы трения покоя
, т.е. когда зазор между поршнем и трубой отсутствует и на поршень действует сила сухого трения. Если действующая на поршень сдвигающая сила F1 мала, то поршень покоится из-за действия силы трения покоя 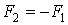 . При переходе F1 через пороговое значение максимальной силы трения покоя, поршень начинает движение и на него действует сила трения скольжения
. При переходе F1 через пороговое значение максимальной силы трения покоя, поршень начинает движение и на него действует сила трения скольжения 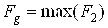 . На рис. 4 показаны зависимости координаты поршня z от времени для различных значений силы Fg. Отметим, что при отсутствии и при наличии силы трения положение точки равновесия будут различными. Это объясняется тем, что в отсутствии трения скорость поршня в первую четверть периода растет, следующую четверть периода уменьшается до нуля, а смещение достигает максимального значения. В течение следующей половины периода скорость отрицательна и в конце поршень доходит до своего первоначального положения. Движение является периодическим с самого начала.
. На рис. 4 показаны зависимости координаты поршня z от времени для различных значений силы Fg. Отметим, что при отсутствии и при наличии силы трения положение точки равновесия будут различными. Это объясняется тем, что в отсутствии трения скорость поршня в первую четверть периода растет, следующую четверть периода уменьшается до нуля, а смещение достигает максимального значения. В течение следующей половины периода скорость отрицательна и в конце поршень доходит до своего первоначального положения. Движение является периодическим с самого начала.
Заключение. В ходе работы было получено, что сила, действующая со стороны жидкости на поршень, может привести как к ускорению, так и к замедлению (вязкое трение) скорости поршня. Наличие сухого трения смещает положение равновесия и сдвиг по фазе относительно фазы градиента давления.
Список литературы:
1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. 6. М.: Наука, 1988. 736 с.
2. Седов Л. И. Механика сплошной среды. Т. 1. М.: Наука, 1970. 492 с.
дипломов


Оставить комментарий