ОПИСАНИЕ  ВОЛН  В  ПРОТЯЖЕННЫХ  СЛОЯХ  ВЛАЖНОЙ  АТМОСФЕРЫ

Ларченко  Инна  Николаевна

аспирантка,  кафедра  теоретической  физики,  Ставропольский  государственный  университет,  г.  Ставрополь

E-mail:  larchenko007@mail.ru

Закинян  Роберт  Гургенович

д.  ф.-м.  н.,  профессор  кафедры  теоретической  физики,  Ставропольский  государственный  университет,  г.  Ставрополь

E-mail:  zakinyan@mail.ru

В  общем  случае  допущение  о  независимости  плотности  воздуха  от  давления  в  протяженных  слоях  атмосферы  не  имеет  места.  Поэтому  можно  говорить  только  об  однородной  атмосфере  с  некоторой  средней  плотностью.

Волны  в  атмосфере  в  этом  случае  описываются  системой  уравнений:

,

.

Решение  данного  уравнения  ищем  в  виде:

.  (1)

Подставляя  данное  решение  в  уравнение  Лапласа,  получим:

,  (2)

где  .  Иначе

.

Общее  решение  данного  уравнения  имеет  вид:

.  (3)

Для  волн  в  протяженной  атмосфере  возмущения  при    (т.е.  к  поверхности  земли)  должны  стремится  к  нулю,  т.е.  .  Этому  условию  удовлетворяет  первое  слагаемое  в  уравнении  (3).  Поэтому  для  волн  в  протяженной  атмосфере  мы  должны  положить:

.  (4)

Тогда  для  потенциала  скорости  запишем  выражение:

.  (5)

Подставляя  это  выражение  в  формулу  (3.1.25),  получим:

  .  (6)

Для  скорости  волны  в  протяженной  влажной  атмосфере  получим  выражение:

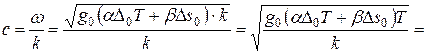
.  (7)

Для  частоты  колебаний  точек  поверхности  волны  получим:

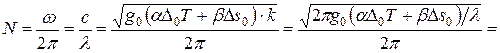
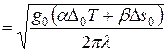.  (8)

Полученные  выражения  для  скорости  волны  и  частоты  колебаний  точек  поверхности  волны  зависят  от  функции  перегрева  и  пересыщения  воздуха.

Из  выражения  (5)  для  потенциала  скорости  следуют  формулы  для  проекций  скорости,  соответственно,  горизонтальной  по  оси    и  вертикальной  по  оси  :

,  (9)

.  (10)

Обе  проекции  скорости  меняются  по  синусоидальному  закону  с  одинаковой  амплитудой  ,  убывающей  с  приближением  к  поверхности  земли.  Однако  в  любой  точке  проекции  скорости  отличаются  фазами  колебаний  [2].  Проекция  скорости  по  оси  отстает  по  фазе  на  90°  от  вертикальной  составляющей  скорости  (что  выражается  множителем  ).  Это  означает,  что  вектор  скорости  вращается  по  часовой  стрелке.  Действительно,  из  формул  (9)  и  (10)  следует,  что  при    и  : 

,

.

Тогда,  для  реальных  частей  этих  выражений  получим:

,  .

Отсюда  видно,  что,  если  в  начальный  момент  времени  имело  место:

,       ,

т.е.  вектор  скорости  был  направлен  вертикально  вверх,  то  в  следующий  момент  времени,  обе  проекции  остаются  положительными,  но  вертикальная  проекция  уменьшается,  а  горизонтальная  проекция  растет,  а  это  возможно,  если  вектор  скорости  вращается  по  часовой  стрелке.  Модуль  скорости  равен:

.  (11)

Частицы  влажного  воздуха  вращаются  по  окружности  радиусом:

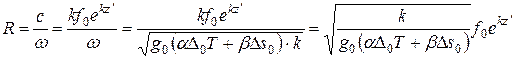.  (12) 

В  невозмущенном  состоянии  атмосферы  изобарическая  поверхность  некоторого  стандартного  уровня  (например,  500  мбар)  ровная.  Так  как  начало  координат  совпадает  с  невозмущенной  поверхностью,  то  для  условия  неглубокой  конвекции  давление  изменяется  по  гидростатическому  закону:

,  (13)

где    –  атмосферное  давление  на  данном  уровне  (500  мбар).  Обозначим  толщину  слоя  атмосферы  .  Тогда  у  земли  при  ,  давление  будет  равно:

,  .

Уравнение  поверхности  запишем  в  виде:

.  (14)

Тогда  давление  возмущенной  атмосферы  будет  равно:

,  (15)

где    –  возмущение  давления,  вызванное  образованием  волны  на  поверхности  уровня.  Так  как  на  поверхности  волны    давление  равно  атмосферному  давлению,  то  отсюда  следует,  что:

.  (16)

Согласно  уравнению  ,  получим:

.  (17)

Согласно  граничному  условию    или  ,  вертикальная  составляющая  скорости  у  плоской  поверхности  земли  равна  нулю:

  или      .  (18)

Так  как

,  (19)

.

Тогда

.

Отсюда  следует,  что:

,             .

Подставляя  полученные  значения  констант  в  формулу  (19),  запишем:

.  (20)

Итак

,  (21)

,  (22)

где  по  определению  гиперболических  функций  записано:

,    .

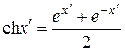Подставляя  выражение  (20)  в  формулу  (17),  получим  дисперсионное  соотношение:

.

Для  поверхности  стандартного  уровня    дисперсионное  соотношение  запишется  в  виде:

,

или

,  (23)

где  по  определению  гиперболического  тангенса  записано  .  Отсюда  для  скорости  волны  во  влажной  атмосфере  получим  выражение:

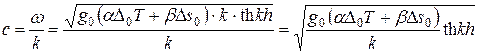.  (24)

Запишем  эту  формулу  в  предельном  случае,  когда  .  Это  значит,  что:

,

т.е.  толщина  слоя  намного  меньше  длины  волны  (условие  длинных  волн  на  поверхности  воды).  Найдем  предел:

.

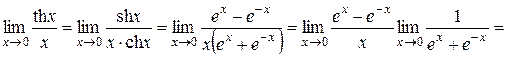
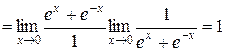Здесь  мы  применили  правило  Лопиталя.  Отсюда  следует,  что  при  малых    имеет  место  приближенное  равенство  .  Тогда  из  формулы  (3.1.49)  следует:

.  (25)

Оценим  значение  скорости  волны  при  следующих  значениях  параметров:  ,  ,  .  Подставляя  численные  значения,  для  скорости  волны  в  сухой  атмосфере  получим  ,  а  для  влажной  атмосферы  .  Для  перегрева    и  пересыщения    скорость  волны  в  сухой  атмосфере  будет  ,  а  во  влажной  –  .  Если  в  формуле  (3.1.50)  допустить,  что  перегрев  равен  нулю,  а  пересыщение  всего  лишь  ,  то  мы  получим  значение  скорости  волны,  вызванной  чисто  пересыщением,  равным  .  Если  бы  мы  применили  известное  выражение  для  скорости  волны  в  баротропной  атмосфере  ,  то  мы  получили  бы  явно  завышенное  значение    [1].

        Из  формулы  (24)  следует,  что  при  ,  т.е.  при    гиперболический  тангенс  порядка  единицы  и  формула  (24)  принимает  вид:

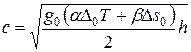.  (26)

Отсюда  следует,  что  для  протяженной  атмосферы,  например  высотой  ,  волна  длинной    при  перегреве    и  пересыщении    движется  со  скоростью  порядка    в  сухой  атмосфере,  а  во  влажной  –  . 

Список  литературы:

1.Грицаева  М.  Н.  Разработка  математической  модели  и  методики  расчета  параметров  атмосферы.  –  Ставрополь,  2011,  168  с.

2.Матвеев  Л.Т.  Физика  атмосферы.  СПб:  Гидрометеоиздат,  2000,  779  с.