ПОСТАНОВКА ЗАДАЧИ ГИДРОУПРУГОСТИ КОЛЬЦЕВОЙ ТРУБЫ ПРИ СВОБОДНОМ ОПИРАНИИ В УСЛОВИЯХ ВИБРАЦИИ

Кондратова Юлия Николаевна

канд. физ.-мат. наук, доцент Саратовский государственный университет, г. Саратов

E-mail: KondratovaUN@info.sgu.ru

Могилевич Лев Ильич

д-р техн. наук, профессор Поволжского филиала МИИТ г. Саратов

Кондратов Дмитрий Вячеславович

д-р физ.-мат. наук, профессор Саратовского государственного технического университета имени Гагарина Ю.А., г. Саратов

Выполнено при поддержке гранта Президента МД-1025.2012.8 и грантов РФФИ 10-01-00177-а, 12-01-31161-мол_а, 12-01-33054-мол_а_вед.

Одной из основных задач современного машино- и агрегатостроения состоит в уменьшении общего веса конструкции при сохранении износоустойчивости при различных внешних воздействиях, вызванных различным факторами. Уменьшение веса конструкции достигается за счет применения тонкостенных конструкций, а поддержание устойчивости к внешним воздействиям использованием жидкости для демпфирования колебаний. Такие конструкции широко применяются в современном железнодорожном, автомобильном и авиационном транспорте, а также ракетно-космических системах [1—3]. Таким образом, практический интерес вызывает построение математических моделей, позволяющих исследовать динамические процессы взаимодействия тонкостенных конструкций и вязкой несжимаемой жидкости.

Рассмотрим трубопроводную систему кольцевого профиля с упругими внутренней и внешней оболочками конечной длины, взаимодействующими с вязкой несжимаемой жидкостью (Рис. 1).

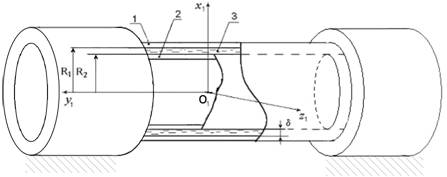
Рисунок1 Физическая модель механической системы

Трубопроводная система состоит из двух упругих соосных цилиндрических оболочек. Обозначим внутренний  и срединной поверхности  радиусы внешней оболочки; внешний радиус  и радиус срединной поверхности  внутренней оболочки. Ширина  цилиндрической щели кольцевого сечения значительно меньше радиуса внутренней оболочки. Толщины внешней  и внутренней  оболочек значительно меньше радиусов их срединных поверхностей  и . Длины оболочек  — одинаковы, а упругие перемещения значительно меньше ширины  цилиндрической щели. Жидкость свободно вытекает из цилиндрической щели. Перемещения внутренней оболочки относительно внешней как твердого тела отсутствуют.

Уравнения Навье — Стокса и уравнение неразрывности для вязкой несжимаемой жидкости с учетом переносного движения основания механической системы в выбранной системе координат , жестко связанной с центром внутренней оболочки, примут вид [2, 3]:

, ,                               (1)

здесь  — давление жидкости;  — плотность жидкости;  — кинематический коэффициент вязкости жидкости; — оператор Лапласа.

Скалярная форма уравнений динамики жидкости (1) имеет вид:

,

,

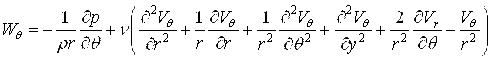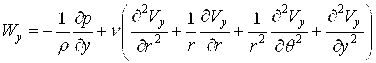,          (2)

,

где

.

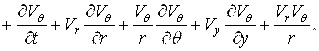
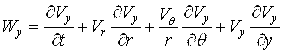Граничные условия для системы уравнений (2) на непроницаемой поверхности в цилиндрической щели запишутся так

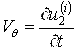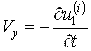, ,  при ,                       (3)

где , .

Кроме того, запишем условия согласования давления:

 при                                                        (4)

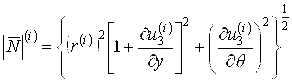
Скалярные уравнения динамики внешней и внутренней упругих цилиндрических оболочек, основанные на гипотезах Кирхгофа-Лява, с учётом переносного движения относительно инерциального пространства, запишутся в виде:

;

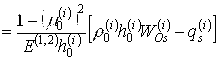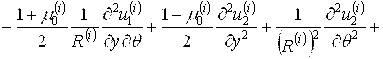
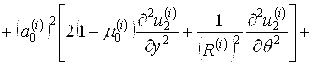                        (5)

,

, .

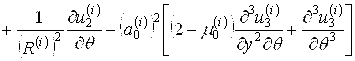
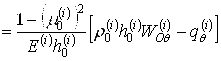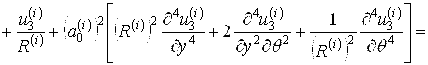
где верхний индекс 1 относится к внешней оболочке, а индекс 2 — к внутренней оболочке;  — модуль Юнга,  — коэффициент Пуассона,  — плотность материала,  — радиус срединной поверхности,  — толщина оболочки,

;

;

; ,

; , ; ; ; ; ;; ; ; ; ; .

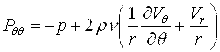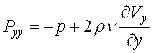В последнем уравнении (5) перед  для внешней оболочки () взят знак минус потому, что жидкость действует на оболочку снизу, для внутренней оболочки () — берется знак плюс.

Граничные условия для перемещений оболочки состоят в условиях свободного опирания:

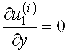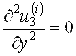, , ,  при .                          (6)

Кроме того, для обеих оболочек ставятся условия периодичности параметров по  с периодом .

Таким образом, получаем математическую модель механической системы, состоящей из двух соосных упругих цилиндрических оболочек, взаимодействующих через слой вязкой несжимаемой жидкости при наличии внешней вибрации.

Список литературы

1.Башта Т.М. Машиностроительная гидравлика ./ Башта Т.М. — М.: Машгиз, 1963.—696 с.

2.Могилевич Л.И. Динамика гироскопов с цилиндрическим поплавковым подвесом./ Андрейченко К.П., Могилевич Л.И..— Саратов: Изд-во. Сарат. ун-та, 1987, 160 с.

3.Могилевич Л.И. Прикладная гидроупругость в машино- и приборостроении/ Могилевич Л.И., Попов В.С. — Саратов: ФГОУ ВПО «Саратовский ГАУ», 2003. — 156 с