Статья опубликована в рамках: VIII Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 26 ноября 2012 г.)
Наука: Информационные технологии
Секция: Методы и системы защиты информации, информационная безопасность
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОДИКА ВЫБОРА ОПТИМАЛЬНОГО НАБОРА СРЕДСТВ ПРОГРАММНО-АППАРАТНОЙ ЗАЩИТЫ ИНФОРИАЦИИ
Хализев Вячеслав Николаевич
канд. техн. наук, профессор КубГТУ, г. Краснодар
Е-mail: ha53@mail.ru
Кузьмин Денис Игоревич
студент КубГТУ, г. Краснодар
Е-mail: kuzmin_ib1@mail.ru
В литературе неоднократно формулировалась задача определения мер и средств защиты как оптимизационная задача выбора при заданных ограничениях, например в [1, с. 4], как задача первого или второго вида. Первая - минимизация стоимости при требуемой эффективности мер защиты и второго вида — максимизация эффективности мер защиты при ограничении на стоимоcть средств.
Между тем, нормативными документами ФСТЭК строго определен порядок построения эффективной защиты — выявление всех возможных угроз безопасности информации, оценка их актуальности, вероятности реализации, определения класса защищенности АС, (либо требуемого уровня защищенности для ИСПДн) и установление по этим данным определенного набора мер соответствия введенному классу защищенности (уровню защиты), то есть третий вид задачи из [1] — покрытия множества требований РД (или угроз) множеством мер и способов защиты (создание профиля функциональных требований (ФТ) защиты — в терминах ГОСТ Р ИСО\МЭК 15408). В этом случае задача количественного определения эффективности и оптимизации стоимости выбранных мер и средств защиты не ставится. При этом отсутствие строгой методики обоснования выбора конкретных мер и способов защиты и реализующих их средств защиты информации (СрЗИ) может привести к неоптимальности, а иногда даже к несостоятельности выбранного далее набора компонентов системы защиты.
Процесс поиска, изучения, анализа и выбора средств достаточно сложен и продолжителен, зависим от уровня знаний специалиста, при этом надо учитывать множество влияющих факторов. Поэтому возможно появление ошибок в силу различных причин, которые могут привести к выбору не лучшего варианта, что может затем сказаться на бюджете и безопасности. Поэтому задача выбора оптимального состава комплекта СрЗИ является актуальной.
Решать эту задачу можно применив систему поддержки принятия решения, базирующуюся на комплексе математических моделей многокритериальной оптимизации.
В [6, с. 55] предлагается оптимизацию выбора СрЗИ проводить по критерию «предпочтительности выбора», вычисляемого как суммарный показатель экспертных оценок обязательных (по функциональным требованиям РД ФСТЭК и ФСБ) и дополнительных показателей, взвешенных коэффициентами важности, по каждому виду СрЗИ в отдельности — защиты от НСД, межсетевым экранам (МЭ), антивирусным средствам (АВС) (по одному средству каждого вида). Эта модель не решает проблемы выбора комплекта СрЗИ когда имеются средства, покрывающие ФТ из разных видов подсистем (известны средства с функциями МЭ, СОВ и АВС одновременно и всеми их сочетаниями), а также внутри одного вида СрЗИ — защиты от НСД, когда одни средства покрывают все ФТ, другие — частично, а некоторые элементы с одним — двумя ФТ (е-токен как электронный ключ, Шипка как электронный ключ и средство хранения сертификатов КриптоПРО)
Решить эту задачу можно применив предлагаемую модель оптимизации, базирующуюся на уточненых моделях многокритериальной оптимизации и методах системного анализа.
Данная модель сочетает принятую парадигму построения CЗИ в виде покрытия набора функциональных требований для класса защищенности АС (уровня защиты ИСПДн) и выработки комплексного показателя защищенности и его оптимизации внутри каждого класса.
Задача выбора оптимальной структуры системы из составляющих ее объектов может быть сформулирована в теоретико-множественной интерпретации как задача о наименьшем покрытии (ЗНП) множества следующим образом [3, с. 1].
Пусть определено множество требований R={r1,r2,…rm} и множество объектов (элементов оборудования) S={S1,S2,…,Sn}, таких, что каждый Sj ассоциирован с подмножеством Rj Í R, где jÎN={1,..,n}, при этом Sj удовлетворяет требованиям из Rj , либо выполняет функцию из Rj.. Совокупность {Rj}, j Î J, JÍN называется покрытием множества R, если È Rj=R, j Î J.
Каждому Rj приписан вес (стоимость) Cj>0. Требуется найти покрытие, имеющее минимальный суммарный вес.
Приведем соответствующую модель целочисленного линейного программирования (ЦЛП). Введем переменные: xj=1, если множество Rj входит в покрытие, иначе xj=0, jÎN. Определим матрицу А=(аij):
|
aij= |
|
Задача выбора оптимального набора объектов S={S1,S2,…,Sn}, при реализации полного набора функций (требований) R={r1,r2,…rm} как задача ЦЛП имеет вид:
|
|
(1) |
при условиях:
|
|
(2)
|
|
|
(3) |
Если Вj интерпретировать как эффективность элементов оборудования, то значения целевой функции (4) определят максимальную эффективность набора оборудования, для построения системы, удовлетворяющей всем заданным требованиям, при тех же ограничениях (2) и (3):
|
|
|
Задача выбора составляющих системы по критерию максимума ее эффективности (4) практически трудно реализуема из-за существенной нелинейности входящих в нее составляющих элементов. Для более точного учета противоречивости предпочтений выбора объектов из S, модифицируем задачу (4), путем ввода матрицы натуральных чисел В:
Определим матрицу В=(bij), iÎM, jÎN :
|
bij = |
|
Пусть величины b определяются экспертным путем, например по методу Саати, методом парных сравнений и нормализации по каждому требованию ri. Если задачи из R имеют разный весовой коэффициент, то вводится вектор a={a1a2….am}, (a1+a2+….+am=1).
Тогда задача выбора оптимального набора объектов S={S1,S2,…,Sn}, для реализации заданных функций (требований) R={r1,r2,…rm} по критерию максимума качества решения задачи ri как задача ЦЛП принимает вид:
|
|
|
При этом фактически, введением матрицы В, мы изменили задачу (2) на задачу многокритериальной дискретной оптимизации (МДО) с критериями вида (5) для каждой функции из R.
При этом в работе [4, с. 59] предложен метод решения задач МДО путем использования нелинейной свертки, чувствительной к упорядочению важности критериев не экспертным путем, а строгим вычислительным алгоритмом, например ЦЛП, применением метода изменения ограничений.
Таким образом, задачу МДО удается свести к итерационному алгоритму А1 следующего вида:
Шаг1: Решить m раз задачу ЦЛП вида (6), при условиях:
 , iÎM (7)
, iÎM (7)
 , iÎM (8).
, iÎM (8).
![]() , jÎN
, jÎN
Шаг 2: Определить вектор X*, при котором
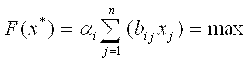
Шаг 3: Вычислить значение точки [Вmin, С*] по формуле (9),
 (9),
(9),
С*=С*+∆; Если С*>Сmax, то стоп, иначе перейти на шаг1.
Этот алгоритм решает задачу МДО методом линейной свертки (анализа иерархий) Саати, скорректированный нелинейной сверткой. В [5, с. 1] доказано, что таким образом множество парето-оптимальных решений сужается до “разумного” многокритериального выбора.
Известна задача МДО, в частности двухкритериальная задача о покрытии множества, в которой требуется найти покрытие одновременно минимизирующее функцию затрат (1) и максимизирующее функцию эффективности, имеющую вид (4) [2, c. 1].
Путем последовательных итераций методом уступок меняя поочереди параметры С и В, предлагается строить парето-оптимальный фронт, из которого ЛПР уже может выбрать решение пользуясь экспертными знаниями.
Практическая реализация алгоритмов А1 в Exel показала практическую возможность решения задач размерностью 100х50 с приемлемой точностью.
Список литературы:
1.Бурушкин А.А., Соловьев С.В., Ступников А.В. Об актуальности разработки методического обеспечения построения комплексных систем защиты информации в системах электронного документооборота при интеграции разноплатформенных программно-технических средств. // Информационное противодействие угрозам терроризма. Научно-практический журнал — 2009. — № 13.
2.Заозерская Л.А., Колоколов А.А. Исследование и решение двухкритериальной задачи о покрытии множества. // Проблемы информатики. — 2009. — № 2 [Электронный ресурс]- Режим доступа — URL: problem-info.ru/2009-2/2.pdf, (дата обращения: 25.10.2012).
3.Львович Я.Е., Чернышева Г.Д., Каширина И.Л., Воронежский государственный технический университет, Воронежский государственный университет- Оптимизация проектных решений в САПР на основе эквивалентных преобразований задачи о минимальном покрытии. Электронное научно-техническое издание № ФС 77-30569. Государственная регистрация № 0421100025 [Электронный ресурс] — Режим доступа — URL: http://technomag.edu.ru/index.html, (дата обращения: 25.06.2012).
4.Ногин В.Д. Границы применимости распространенных методов скаляризации при решении задач многокритериального выбора // Методы возмущений в гомологической алгебре и динамика систем: Межвуз. сб. науч. тр. Саранск: Изд-во Мордов. ун-та, 2004, С. 59—68.
5.Ногин В.Д., Басков О.В. Сужение множества Парето на основе учёта произвольного конечного набора числовой информации об отношении предпочтения // Доклады АН, 2011, т. 438, № 4, С. 1—4.
6.Прокушева А.П., Прокушев Я.Е. Моделирование и оптимизация выбора средств программно-аппаратной защиты информации с точки зрения экономической и технической целесообразности. // Информация и безопасность — 2012. — № 1. С. 55—60.
дипломов

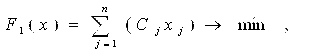
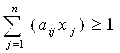 , где iÎM
, где iÎM ,
,
Оставить комментарий