МОДЕЛИРОВАНИЕ ВЕТВИ НАМАГНИЧИВАНИЯ СИЛОВОГО ТРАНСФОРМАТОРА ПРИ ГЕОМАГНИТНЫХ БУРЯХ В МАТЕМАТИЧЕСКОЙ СРЕДЕ MATLAB

Вахнина Вера Васильевна

канд. техн. наук, доцент, зав. кафедрой «Электроснабжение и электротехника», Тольяттинского государственного университета, г. Тольятти

Е-mail: vvvahnina@yandex.ru

Черненко Алексей Николаевич

канд. техн. наук, доцент кафедры «Электроснабжение и электротехника», Тольяттинского государственного университета, г. Тольятти

Е-mail: tchernenko83@yandex.ru

Кретов Дмитрий Алексеевич

аспирант кафедры «Электроснабжение и электротехника», Тольяттинского государственного университета, г. Тольятти

Е-mail: dmitry.kretov@gmail.com

Кузнецов Виталий Александрович

аспирант кафедры «Электроснабжение и электротехника», Тольяттинского государственного университета, г. Тольятти

Е-mail: V.A.Kuznetcov@yandex.ru

Во время геомагнитной бури (ГМБ) на поверхности Земли возбуждается медленно меняющееся геоэлектрическое поле напряженностью 1—20 В/км и периодом до 30 минут [7]. Между заземленными точками нейтралей силовых трансформаторов подстанций систем электроснабжения (СЭС) появляется значительная разность потенциалов, и по электрическим сетям циркулируют практически постоянные — геоиндуцированные токи (ГИТ). Основное воздействие ГИТ на СЭС заключается в насыщении магнитопроводов силовых трансформаторов (СТ), в результате чего возрастают несинусоидальные намагничивающие токи, которые также циркулируют по электрической сети. В СЭС увеличивается потребление реактивной мощности и снижается пропускная способность сети, происходит падение напряжения, появляются высшие гармонические составляющие тока и напряжения, возможны ложные срабатывания релейной защиты и автоматики, и, как следствие, нарушение нормальной работы потребителей [3]. Поэтому при моделировании режимов работы СЭС при геомагнитных бурях в модели силового трансформатора необходимо учитывать нелинейность ветви намагничивания [1].

Для моделирования режимов работы СЭС при геомагнитных бурях авторами используется матричная математическая система MATLAB. Система стала мировым стандартом в области современного математического и научно-технического программного обеспечения [5, 6].

Трехфазный двухобмоточный трансформатор в среде MATLAB моделируется на основе Т-образной схемы замещения, представленной на рис. 1 [6].

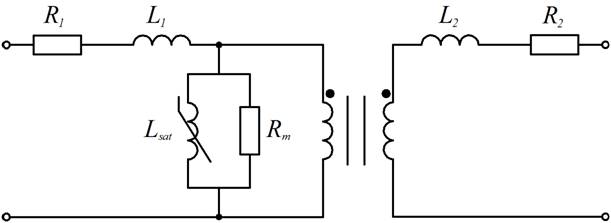
Рисунок 1. Схема замещения двухобмоточного трансформатора в среде MATLAB

На схеме замещения (рис. 1): R₁ и R₂ — активные сопротивления, учитывающие потери активной мощности в первичной и во вторичной обмотках трансформатора при протекании по ним соответствующих рабочих токов; L₁ и L₂ — индуктивности первичной и вторичной обмоток от полей рассеяния силового трансформатора; R_m — активное сопротивление ветви намагничивания, учитывающее потери активной мощности в магнитопроводе трансформатора от основного магнитного поля; L_sat — индуктивность ветви намагничивания, учитывающая нелинейность трансформатора.

В [1] установлено, что при геомагнитных бурях взаимная индуктивность ветви намагничивания силового трансформатора связана зависимостью магнитной проницаемости магнитопровода силового трансформатора от протекающего в обмотке тока намагничивания, который при ГМБ является функцией от ГИТ:

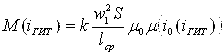,                                        (1)

где w₁ — число витков обмотки ВН;  — площадь поперечного сечения сердечника; l_ср — средняя длина магнитной линии;  — эмпирический коэффициент, зависящий от конструкции трансформатора.

Функция  определяется из кривой намагничивания B=f(H), которая в общем случае нелинейна и зависит от величины геоиндуцированного тока. При возрастании ГИТ и насыщении магнипровода СТ магнитная проницаемость сердечника уменьшается в десятки раз и в пределе стремится к единице.

Однако, при исследовании процессов насыщения магнитопроводов СТ при ГМБ, возникают затруднения. В среде MATLAB для моделирования силовых трансформаторов используется функция Ψ(i₀) (рис. 2), которая задается по четырем точкам и соответствует силовому трансформатору ТДЦ ‑ 250000/735/315.

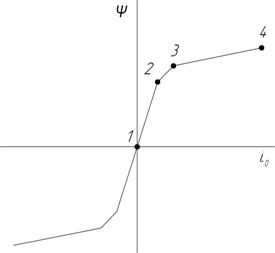
Рисунок 2. Задаваемая в среде MATLAB функция Ψ(i₀) для силового трансформатора ТДЦ-250000/735/315

Использование кривой Ψ(i₀) в относительных единицах при задании индуктивности ветви намагничивания для силовых трансформаторов других классов напряжения и мощности приводит к искажению результатов моделирования СЭС при геомагнитных бурях.

Предлагается кривую Ψ(i₀) определять из кривой намагничивания  с помощью упрощенной гистерезисной модели магнитного сердечника силового трансформатора с использованием основных параметров петли магнитного гистерезиса: коэрцитивной силы H_c, остаточной индукции B_r и индукции насыщения B_s [2]:

для восходящего участка

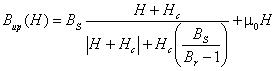                                                           (1)

и для нисходящего участка

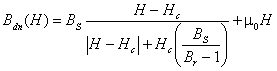.                                                          (2)

Начальная кривая моделируется выражением:

.                                                                               (3)

Для моделирования кривой Ψ(i₀) используется 150—200 значений (рис. 3).

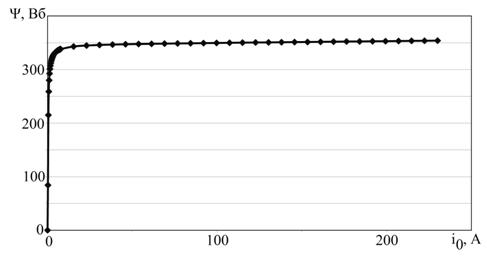
Рисунок 3. Смоделированная начальная кривая Ψ(i₀) намагничивания сердечника силового трансформатора

Для расчета взаимной индуктивности ветви намагничивания силовых трансформаторов должны быть заданы:

·конструктивные параметры силового трансформатора: сечение стержня магнитопровода S, средняя длина магнитного потока магнитопровода l_ср, количество витков обмотки высокого напряжения w₁;

·параметры петли магнитного гистерезиса стали магнитопровода силового трансформатора: коэрцитивная сила H_c, остаточная индукция B_r и индукция насыщения B_s для моделирования кривой намагничивания B=f(H);

·параметры схемы замещения СЭС (паспортные электрические параметры силового трансформатора и линии электропередачи, сопротивления заземляющего устройства и грунта и др.);

·напряженность геоэлектрического поля Е.

Алгоритм расчета взаимной индуктивности M(i_ГИТ) реализован с помощью математического пакета MATLAB (рис. 4).

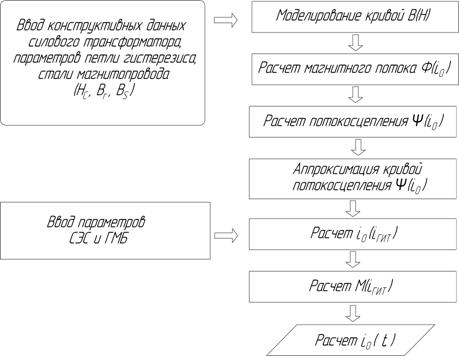
Рисунок 4. Алгоритм расчета нелинейной взаимной индуктивности силовых трансформаторов при геомагнитных бурях

Выполнено моделирование режимов работы силового трансформатора ТРДН-63000/110/6,3/6,3 (схема соединения обмоток Yн/∆/∆) в нормальном режиме при отсутствии ГИТ и при геомагнитных бурях со стандартной кривой Ψ(i₀) и уточненной по алгоритму, приведенному на рис. 4. Результаты моделирования приведены на рис. 5, 6.

При использовании кривой Ψ(i₀) из стандартной модели силового трансформатора ток холостого хода является синусоидальным (рис. 5, а), т. к. рабочая точка не выходит за пределы участка 1—2 (рис. 2). При использовании уточненной модели СТ кривая тока холостого хода соответствует действительной (рис. 5, б) [4].

При расчете процессов насыщения магнитопровода силового трансформатора при протекании ГИТ по обмотке ВН с использованием кривой Ψ(i₀) из стандартной модели амплитудное значение тока намагничивания в 1,5 раза ниже значения (рис. 6, а), полученного с использованием кривой Ψ(i₀) из уточненной модели СТ (рис. 6, б). Также следует отметить, при расчете процесса насыщения магнитопровода СТ при протекании ГИТ по его обмоткам необходимо более точное описание участка перегиба кривой намагничивания.

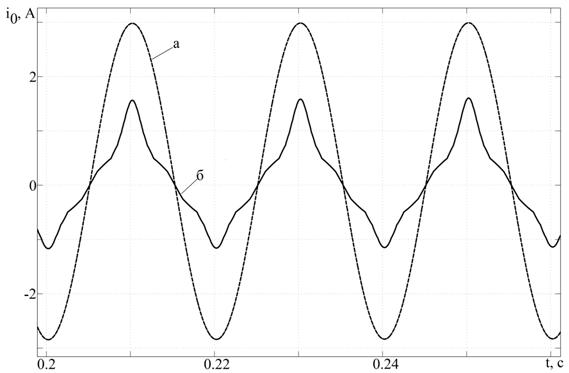
Рисунок 5. Ток холостого хода силового трансформатора ТРДН-63000/110/6,3/6,3 при использовании кривой намагничивания из стандартной (а) и уточненной (б) модели СТ в MATLAB

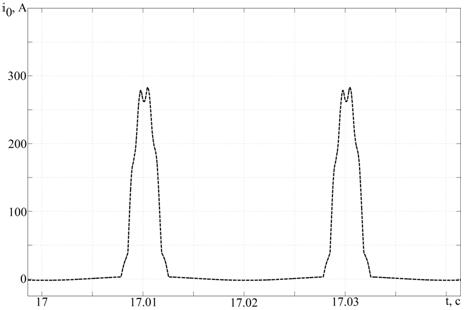
а)

б)

Рисунок 6. Ток намагничивания силового трансформатора ТРДН-63000/110/6,3/6,3 при геомагнитных бурях при использовании кривой намагничивания из стандартной (а) и уточненной (б) модели СТ в MATLAB

Получено, для моделирования процессов в СЭС при геомагнитных бурях в среде MATLAB необходимо учитывать нелинейность взаимной индуктивности ветви намагничивания, которая определяется, как конструктивными параметрами силового трансформатора и параметрами кривой намагничивания его магнитопровода, так и параметрами геоэлектрического поля. Применение уточненной модели силового трансформатора позволяет получить расчетные значения тока намагничивания, близкие к реальным.

Список литературы:

1.Вахнина В.В., Черненко А.Н., Кузнецов В.А. Влияние геоиндуцированных токов на насыщение магнитной системы силовых трансформаторов // Вектор науки Тольяттинского государственного университета. 2012. № 3(21). С. 65—69.

2.Володин В. Гистерезисная модель нелинейной индуктивности симулятора LTspise // Силовая электроника. 2010. № 1. С. 56—60.

3.Гершенгорн А.И. Воздействия геомагнитных токов на электрооборудование энергосистем // Электрические станции. 1993. № 6. С. 54—3.

4.Петров Г.В. Электрические машины: в 3-х частях. Ч. 1. Введение. Трансформаторы. М.: Энергия, 1974. — 240 с.

5.Смоленцев Н.К. MATLAB: программирование на Visual C#, Borland C#, JBuilder, VBA. М.: ДМК-Пресс, 2011. — 456 с.

6.Черных И.В. Моделирование электротехнических устройств в MATLAB, SimPowerSystems и Simulink. М.: ДМК Пресс, 2008. — 290 с.

7.Key A.J. Geoelectric Fields and Geomagnetically Induced Currents in the United Kington / University of Edinburgh. 2003. — 260 p.