ФОРМИРОВАНИЕ ОПТИМАЛЬНОГО СЕМЕЙСТВА МАРШРУТОВ ШКОЛЬНЫХ АВТОБУСОВ

Назмутдинова Айгуль Венеровна

выпускник УГАТУ по специальности «экономист-математик», г. Уфа

E-mail: nav40162@gmail.com

Уже на протяжении многих десятилетий оптимизационным задачам уделяется значительное внимание. К ним относят также задачи в области логистики. Логистика — это процесс планирования, обеспечения и контроля эффективного поступления товаров, услуг и сопутствующей информации из места производства к месту потребления, с целью удовлетворить потребности целевой группы. Минимизация временных затрат является актуальным решением проблемы в условиях перевозки пассажиров, в особенности школьников (соблюдение санитарных норм). Кроме того, в сложившейся на сегодняшний день экономической ситуации, когда не каждая семья имеет возможность владеть индивидуальным видом транспорта, организуемый и контролируемый перевоз детей является адекватным решением проблемы [2, c. 96].

Задача о школьном автобусе впервые была поставлена в 1969 г. математиками Р.М. Ньютоном и В.Х. Томасом (SBRP — School Bus Routing Problem). В данной статье рассматриваются два метода решения задачи, позволяющие минимизировать время движения и сформировать маршруты транспортных средств.

В качестве элементов задачи о школьном автобусе выступают:

1.         транспортные средства (автобусы);     

2.         пассажиры (ученики);

3.         базовое депо (школа);

4.         множество остановок, где должны выйти ученики.

Кроме того, в качестве входных данных используются также количество пассажиров, которое необходимо высадить на каждой остановке; вместимость автобусов (рассмотрен случай, когда все автобусы имеют одинаковую вместимость); время проезда от одной остановки до другой [3].

Неизвестным является количество учеников, которое каждый автобус высаживает на каждой остановке (возможна ситуация, что на каждую остановку студентов можно доставить на разных автобусах). И впоследствии строится маршрут каждого автобуса.

Математически формализовать задачу можно следующим образом: Пусть G=(S,A) — исходный ориентированный граф, в котором S={0,..,n} — множество вершин (остановок), причем О_ой пункт — это школа.

Дано:

S_i — автобусная остановка (i=1,..,n),

где    n — количество остановок.

0_ой пункт — база, откуда отходят все автобусы с пассажирами (школа).

D_i — число пассажиров, которое необходимо высадить на i-й остановке(i=1,..,n).

A_ij — время движения от i-й до j-й остановки (i,j=1,..,n).

T^k — вместимость k-го автобуса, где k=1,..,K — количество имеющихся автобусов.

Неизвестные параметры:

P_i^k — количество пассажиров, которое k-й автобус высаживает на i-ой остановке.

С(R^k) — время, которое k-й автобус затрачивает на свой маршрут с целью развезти пассажиров по остановкам, где R^k — подмножество остановок, которые проезжает k-й автобус на своем пути, R^k={i: P_i^k >0}

Ограничения:

1.         Суммарное число пассажиров, которое автобусы высаживают на i-й остановке должно быть равно числу пассажиров, которое необходимо доставить на i-ю остановку:

                                                      (1)

2.         Суммарное число пассажиров, попавших в k-й автобус не может превышать вместимости данного автобуса:

                                                   (2)

3.         Со всех k=1,..,K автобусов пассажиры только высаживаются на остановках i=1,..,n:

,

где P_i^k — целые                  (3)

Целевая функция: max{С(R^k)} → min

т. е. необходимо минимизировать время высадки самого последнего пассажира на последней остановке в маршруте самого «долгого» автобуса. Под маршрутом автобуса k понимается цепь остановок, которые данный k-й автобус проезжает, высаживая пассажиров на каждой из посещаемых, за исключением 0-го пункта (базы/школы), откуда начинается непосредственное движение автобуса. Из 0-го пункта отправляются все пассажиры и никто не высаживается [1, с. 139].

Вторая математическая модель имеет следующий линейный вид: введем новую булеву переменную Y_i^k такую, что:

                                                       (4)

Таким образом, если Y_i^k =1, это говорит о том, что k-ый автобус высаживает на i-ой остановке пассажиров. В противном случае, Y_i^k =0.

Количество пассажиров, которое k-й автобус высаживает на i-й остановке не может превосходить вместимости k-го автобуса, согласно условию (2), тогда  [0;1]. Для введенной булевой переменной будет справедливо следующее неравенство:

                                          (5)

где    i=1,..,n и k=1,..K.

Введем следующую булеву переменную  такую, что:

 =                 (6)

где u,v=0,..,n

Если k-й автобус после u-ой остановки заезжает v-ую остановку, он должен будет в v-ой остановке обязательно высадить пассажиров. Таким образом, справедливы следующие ограничения (7.1) — (8.2). При этом важно отметить, что мы рассматриваем ситуацию, когда автобусы после отправления из 0-го пункта и проезда через все остановки в соответствующих маршрутах необязательно возвращаются в 0-ой пункт (рассматривается цепь, а не цикл остановок в маршруте). Таким образом, необходимо исключить вариант, где в качестве v-ой остановки выступает 0-ой пункт.

                                                  7.1)

                                                  (7.2)

Z₀₀^k=0                                                                   (7.3)

Для любого k-го автобуса, отправляющегося из 0-го пункта справедливо, что он может попасть в v-ую остановку (8.1), но не сможет вернуться в 0-ой пункт (базу) — (8.2)

                                                     (8.1)

                                                     (8.2)

Кроме того, количество ветвей между остановками, которые посещает k-ый автобус последовательно, направляясь из u-ой остановки в v-ую, будет равно общему количеству посещенных остановок, на которых k-ый автобус высаживает пассажиров за вычетом 1. (основываясь на правиле, что число связей между вершинами в цепи равно w=f-1, где w — количество связей(ветвей), f — количество вершин(остановок):

                                              (9)

Введем целочисленные переменные  (u=0,..n) такие, что:

                                                    (10)

                                                  (11)

Переменные  имеют смысл номеров остановок в порядке прохождения в маршруте автобуса.

Время, которое затрачивают все автобусы на то, чтобы развезти всех пассажиров на остановки не превышает некого t , где t — новая переменная:

                                      (12)

где с_uv — это время, затрачиваемое на перевоз пассажиров от остановки u до v

Тогда целевая функция в нашей задаче примет следующий вид:

t + max { 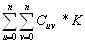,1}*→min           (13)

Таким образом, мы составили две модели: линейную и нелинейную. Методы, применяемые для решения задачи, естественным образом будут отличаться друг от друга. Сначала рассмотрим методы решения линейной задачи [5].

Сформулировав линейную целочисленную задачу, мы можем применить точные методы, которые, в свою очередь, гарантируют нахождение оптимального решения. Кроме точных методов существуют аппроксимирующие, эвристические методы. Но, безусловно, нахождение оптимального решения проблемы является главным достоинством точных методов. Однако, имея дело с большой размерностью, попытка полного перебора решений не даст необходимого результата даже на самых современных компьютерах. Произведена попытка определить эти границы «перехода» от решения линейной к нелинейной задаче. Схема проведенной работы выглядит следующим образом: на первом шаге строится матрица кратчайших путей (времени) от i остановки до j. На втором шаге, если решается нелийнейная задача, применяется новый эвристический метод гармонического поиска, а в случае линейной задачи — метод ветвей и границ. Точный метод ветвей и границ позволяет найти оптимальное решение — маршруты школьных автобусов. Но при этом нахождение решения возможно лишь при малой размерности (пример 1, количество остановок = 3). В реально жизни мы сталкиваемся с проблемами, где размерность задачи намного больше. При количестве остановок равным 8 математическая среда Matlab, где производились вычисления, не справилась с решением данной задачи за выделенное компьютером время. Расчет производился более 6000 секунд, после чего происходит прерывание и выдача ошибки: «Превышение временного лимита вычисления». Таким образом, можно сделать вывод, что при реальной размерности задачи, точные методы не разрешают проблемы, и приходится обращаться к эвристическим методам.

Как было отмечено, для решения задачи применяется относительно новый эвристический алгоритм Harmony Search, разработанный в 2005 году [4]. Отличительная черта его адаптации к этой задаче о школьном автобусе заключается в том, что в русской литературе еще не встречалось аналогов применения. Достоинство любой эвристики — быстрота вычисления при любой размерности. Но главный недостаток заключается в том, что, к сожалению, применяя эвристические алгоритмы, не удается найти оптимальное решение, а только допустимое. Таким образом, невозможно гарантировать правильность выбора маршрутов школьных автобусов, используя эвристику. Но на сегодняшний день это единственная возможность получить решение такого типа задач — использование эвристических алгоритмов.

Список литературы:

1.Лукинский В.С., Лукинский В.В., Пластуняк И.А., Плетнева Н.Г.: Транспортировка в логистике: учеб. пособ. / Спб.:СПбГИУЭ, 2005. — 139 с.

2.Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике: учебное пособие. СПб.: Изд-во СПбГУЭФ 2010 — 96 с.

3.Dantzig G. B., Fulkerson D.R, Johnson S.M.: Solution of a large-scale traveling salesman problem, Oper. Res.,2(1954), p. 393—410.

4.Geem Z.W.: School Bus Routing using Harmony Search, Johns Hopkins University, Rockville, p. 1—6.

5.Goldberg D.E.: Genetic Algorithms in Search Optimization and Machine Learning. Addison Wesley, MA, 1989.