Статья опубликована в рамках: VI Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 25 сентября 2012 г.)
Наука: Информационные технологии
Секция: Системный анализ, управление и обработка информации
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ ОТКАЗОУСТОЙЧИВОСТИ СИСТЕМ УПРАВЛЕНИЯ НЕПРЕРЫВНЫМИ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ
Кораблев Юрий Анатольевич
канд. техн. наук, доцент каф АПУ, СПбГЭТУ, г. Санкт-Петербург
E-mail: Korablev@pochta.tvoe.tv
Шестопалов Михаил Юрьевич
канд. техн. наук, проректор по научной работе, доцент каф. АПУ, СПбГЭТУ, г. Санкт-Петербург
В статье для решения задачи определения множества потенциально возможных отказов технологического оборудования предлагается подход на основе обобщенной методологии, построенной по принципу эволюционного исследования сложных систем [3, 4] с привлечением классических статистических и нечетких технологий [1, 7, 9], позволяющей упорядочить процесс анализа в виде поэтапной процедуры, организованной иерархически.
Организационную последовательность проведения исследований можно представить в виде трех этапов.
I. Этап сбора экспериментальных данных для построения топологической модели непрерывного технологического процесса
II. Нечеткая топологическая идентификация
Выходным результатом этого этапа является ориентированный нечеткий граф модели технологического процесса, т. е. модель первого ранга неопределенности. Представление модели в виде нечеткого графа в рамках предлагаемой процедуры имеет свои особенности.
Традиционно нечеткий ориентированный граф определяется как граф ![]() , у которого
, у которого ![]() — четкое множество вершин, а
— четкое множество вершин, а ![]() — нечеткое множество ребер, где
— нечеткое множество ребер, где ![]()
![]() — значение функции принадлежности
— значение функции принадлежности ![]() для ребра
для ребра ![]() .
.
Здесь целесообразно рассматривать множество вершин графа также как нечеткое множество, т. е. ![]() ,
, ![]() — нечеткое множество вершин и
— нечеткое множество вершин и ![]() .
.
Топология объекта включает в себя множество координат и множество отношений между ними. Определение наличия этих отношений является целью нечеткой топологической идентификации. Таким образом, процесс построения топологии модели естественным образом разбивается на:
1. проверку координат на изолированность
2. проверку координат на наличие связи
3. ориентацию связи
Процедуры проверки координат на изолированность и наличие связи предполагают формирование матрицы корреляции R:

состоящей из парных коэффициентов корреляции (ПКК), учитывающих тесноту линейной корреляционной связи между всеми парами координат с учетом их взаимного влияния и взаимодействия. Коэффициент корреляции между каждой парой координат X и Y ![]() рассчитывается по формуле:
рассчитывается по формуле:
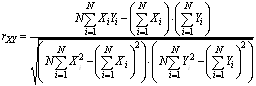
Для проверки координат на изолированность на основе матрицы корреляции рассчитывается для каждой координаты множественный коэффициент корреляции (МКК) ![]() , характеризующий степень тесноты связи между координатой и всеми остальными независимыми переменными:
, характеризующий степень тесноты связи между координатой и всеми остальными независимыми переменными:

где ![]() — определитель матрицы корреляции,
— определитель матрицы корреляции,
![]() — алгебраическое дополнение матрицы корреляции для исследуемой координаты.
— алгебраическое дополнение матрицы корреляции для исследуемой координаты.
Величина МКК лежит в пределах 0£![]() £1. При этом идеальными с точки зрения процедуры проверки являются крайние точки диапазона. При значении 0 для МКК делается вывод, что координата изолированная. При значении МКК=1 является справедливым альтернативное утверждение.
£1. При этом идеальными с точки зрения процедуры проверки являются крайние точки диапазона. При значении 0 для МКК делается вывод, что координата изолированная. При значении МКК=1 является справедливым альтернативное утверждение.
Для проверки на наличие связи на основе матрицы корреляции рассчитывается для каждой пары координат частный коэффициент корреляции (ЧКК) ![]() , характеризующий тесноту линейной корреляционной связи между парой анализируемых координат
, характеризующий тесноту линейной корреляционной связи между парой анализируемых координат ![]() и
и ![]() без учета влияния на эту пару других переменных
без учета влияния на эту пару других переменных ![]() ,
,![]() и т. д. В матричном виде формула для расчета частных коэффициентов корреляции выглядит следующим образом:
и т. д. В матричном виде формула для расчета частных коэффициентов корреляции выглядит следующим образом:
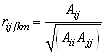 ,
,
где ![]() ,
, ![]() ,
, ![]() — алгебраические дополнения соответствующих элементов матрицы парных корреляций R.
— алгебраические дополнения соответствующих элементов матрицы парных корреляций R.
Величина ЧКК лежит в пределах —1£![]() £1. Значение ЧКК, равное 0, говорит об отсутствии связи между координатами, 1 — о положительной функциональной зависимости, —1 — о полной обратной линейной связи.
£1. Значение ЧКК, равное 0, говорит об отсутствии связи между координатами, 1 — о положительной функциональной зависимости, —1 — о полной обратной линейной связи.
Для оценки значимости МКК и ЧКК применяют два подхода.
Первый подход базируется на применении методов математической статистики [5, 6]. В рамках этого подхода требуется оценить значимость выборочной величины коэффициента или, в соответствии с постановкой задач проверки статистических гипотез, проверить гипотезу о равенстве нулю соответствующего коэффициента корреляции. Если гипотеза Н0 о равенстве нулю коэффициента корреляции будет принята, то оценка коэффициента не значима, и делается вывод об изолированности координаты для МКК и отсутствии связи для ЧКК. Если гипотеза Н0 будет отвергнута, то выборочный коэффициент значим, справедливы альтернативные предположения.
Для МКК в качестве критерия проверки нулевой гипотезы Н0 применяют критерий Фишера
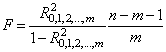 ,
,
где m — число координат,
n — объем выборки.
Проверка гипотезы Н0 о равенстве нулю МКК проводится следующим образом. Фактическое значение частного F-критерия сравнивается с табличным значением распределения Фишера при заданном уровне значимости ![]() . Если фактическое значение превышает табличное, то включение координаты xi в модель статистически оправданно. Если же фактическое значение меньше табличного, то нецелесообразно включение этой координаты в модель, координата изолирована.
. Если фактическое значение превышает табличное, то включение координаты xi в модель статистически оправданно. Если же фактическое значение меньше табличного, то нецелесообразно включение этой координаты в модель, координата изолирована.
Для ЧКК как критерий проверки нулевой гипотезы Н0 применяют:
 ,
,
где k — число пассивных координат,
n — объем выборки.
Величина t при справедливости нулевой гипотезы распределена по закону Стьюдента с n-к-2 степенями свободы. Конкурирующая гипотеза Н1 соответствует утверждению, что значение ![]() не равно нулю. Проверка гипотезы Н0 о равенстве нулю ЧКК двумерной нормально распределенной случайной величины проводится аналогично проверке равенства нулю МКК.
не равно нулю. Проверка гипотезы Н0 о равенстве нулю ЧКК двумерной нормально распределенной случайной величины проводится аналогично проверке равенства нулю МКК.
Таким образом, данный подход находится фактически в русле классической логики: решение по каждой координате или связи принимается по принципу «нет/да». Но так как при этом вводится вероятностная оценка, то в полученной топологической модели в форме нечеткого графа значения функций принадлежности для всех ребер и вершин будут равны 1-a.
Процедура ориентации связей, т. е. проведение причинно-следственного анализа может осуществляться разными способами:
1. Сравнение интервалов корреляций взаимнокорреляционных функций для каждой пары координат
Это подход основан на выявлении временной задержки, возникающей при прохождении сигнала по ориентируемой динамической связи, что проявляется в несимметричности взаимных корреляционных функций для любой пары координат. Правило для ориентации связи:
Если ![]() , тo
, тo ![]() ,
,
где ![]() ,
, ![]() — интервалы корреляции для взаимнокорреляционный функций
— интервалы корреляции для взаимнокорреляционный функций ![]() и
и ![]() соответственно.
соответственно.
2. Перекрестно-отсроченные корреляции (ПОК) Кэмпбелла [8]
Для анализа методом ПОК две переменные должны быть измерены несколько раз через один и тот же промежуток времени. В основе данного метода лежит положение о том, что если А — более сильная причина В, чем наоборот, то можно ожидать, что коэффициент корреляции ![]() больше, чем
больше, чем ![]() ,
, ![]() больше, чем
больше, чем ![]() и т. д.
и т. д.
3. Причинный анализ сопутствий в непрерывных временных сериях
Основан на следующем положении: X можно рассматривать как причину Y, если она вносит вклад в предсказание Y свыше того, которое дает упорядоченное поведение самого Y. Применяя приемы перекрестно-отсроченных корреляций к временным сериям, можно попытаться установить направленность причинно-следственных связей (X→Y или Y→X). Это осуществляется путем сравнения перекрестно-отсроченных корреляций, когда X упреждает Y и когда Y упреждает X на 1, 2...n сдвигов.
4.Путевой анализ
Путевой анализ состоит в построении схем, изображающих систему корреляционных отношений в виде путевых диаграмм.
Если в рассматриваемых подходах корреляционную связь нельзя считать линейной, что справедливо в случаях заметных отклонений распределений вероятностей исследуемых координат от нормальных, то в основу предлагаемой методики должно быть положено корреляционное отношение.
Корреляционное отношение — это отношение двух средних квадратичных отклонений, одно из которых характеризует часть изменчивости первого признака, обусловленную его зависимостью от второго признака, а второе является обычной мерой общей изменчивости первого признака:
![]()
![]()
Второй подход базируется на применении методов нечеткой логики. В этом случае исходят из качественной оценки тесноты связи между каждой координатой и всеми остальными (при проверке на изолированность) или между каждой парой координат (при проверке на наличие связи).
Для качественной оценки тесноты связи на основе МКК И ЧКК можно использовать следующую классификацию, часто применяемую на практике:
· 0.0 — нет связи (точно нет);
· 0.25 — слабая связь (скорее нет, чем есть);
· 0.5 — неопределенная связь (трудно отнести к слабой или сильной);
· 0.75 — возможная связь (скорее есть, чем нет);
· 1.0 — есть связь (точно есть) ;
Это экспертное представление о тесноте связи позволяет построить механизм нечетких логических выводов для оценки нечеткой вероятности (значения функции принадлежности) наличия координаты и связи в нечетком графе, представляющем топологическую модель технологического процесса.
Входной лингвистической переменной R в процедуре проверки координаты на изолированность является МКК, а в процедуре проверки на наличие связи модуль ЧКК со следующими нечеткими значениями (термами):
· Ноль (Z);
· Меньше половины (LTH);
· Половина (H);
· Больше половины (MTH);
· Единица (O);
Начальное распределение термов входной переменной R показано на рис. 1:

Рисунок 1. Начальное распределение термов входной переменной R
В рамках данной методики целесообразно сохранить информацию о знаке ЧКК, т. е. о характере линейной связи: о положительной функциональной зависимости или о полной обратной линейной связи.
Выходной лингвистической переменной P будет нечеткая вероятность наличия координаты при проверке на изолированность и тесноты связи при проверке наличия связи:
· Нет связи (N)
· Слабая связь (WC)
· Неопределенная связь (UC)
· Возможная связь (PC)
· Есть связь (E)
Начальное распределение термов выходной переменной P показано на рис. 2:
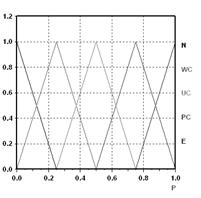
Рисунок 2. Начальное распределение термов выходной переменной P
База правил имеет вид:
ЕСЛИ R=Z ТО P=N
ЕСЛИ R=LTH ТО P=WC
ЕСЛИ R=H ТО P=UC
ЕСЛИ R=MTH ТО P=PC
ЕСЛИ R=O ТО P=E
Полученные значения нечеткой вероятности устанавливаются на вершинах и дугах нечеткого графа, причем на дугах с учетом знака ЧКК для пары координат, которые они соединяют.
Механизм нечетких логических выводов может быть реализован по схеме MAX-MIN или МАХ-PROD. В качестве метода дефазификации целесообразно использовать модифицированный метод центра тяжести.
III. Анализ возникновения потенциальных отказов на основе нечеткого ориентированного графа технологического процесса
Идея анализа основывается на рассмотрении нечеткого ориентированного графа технологического процесса как нечеткой когнитивной карты (Fuzzy Cognitive Maps), введенной Коско [10]. В когнитивном анализе решаются два типа задач: статические и динамические. Статический анализ — это анализ путей влияния одних факторов на другие. Динамический анализ — это генерация и анализ сценариев развития ситуации во времени.
Среди координат процесса выделяются управляющие и регулируемые, изменение или стабилизация которых является целью управления. Путем внесения в нечеткую когнитивную карту отказа оценивается степень влияния управляющих координат на регулируемые, что классифицирует отказ как:
· несущественный, не требующий коррекции
· компенсируемый полностью
· компенсируемый с потерей качества управления
· фатальный, когда коррекция не является возможной
Отказы моделируются на топологическом уровне изменением величины нечетких вероятностей:
1. Выпадение (или ослабление влияния) вершин графа.
2. Выпадение (или ослабление силы) связи между вершинами графа.
Физическая интерпретация каждого конкретного топологического отказа возлагается на экспертов в данной предметной области исследований.
Задача может решаться статически: путем расчета и анализа выбранных системных показателей нечеткой когнитивной карты (взаимных консонансов, диссонансов, положительных и отрицательных влияний концептов друг на друга и на систему в целом). Но более предпочтительно использование динамического анализа, т. е. анализ когнитивной карты во времени.
Базовым элементом нечеткой когнитивной карты [2] является связь, описывающая влияние одного концепта Кi на другой Кj. Направленность связи wij означает, что концепт-источник влияет на концепт-приемник. При положительной связи и увеличении концепта Кi Кj увеличивается, при уменьшении Кi Кj уменьшается. При отрицательном значении связи увеличение значения Кi вызовет уменьшение Кj и наоборот. Влияния входных концептов суммируются и для предотвращения выхода за пределы диапазона выходного концепта используется специальная нелинейная функция f:
![]()
где wij — вес влияния концепта i на концепт j,
N — число концептов, влияющих на концепт j,
Ki и Kj — значения входного и выходного концептов.
Нелинейная функция f [·] используется для нормализации вычислений в диапазоне [0, 1]. Обычно используется сигмоидальная функция:
![]() , λ>0
, λ>0
Функционирование нечеткой когнитивной карты в дискретном времени:
![]()
Если в нечеткой когнитивной карте имеются петли обратной связи, то:
 .
.
Список литературы:
1.Алексеев А.А., Кораблев Ю.А., Шестопалов М.Ю. Идентификация и диагностика систем. М.: Издательский центр «Академия», 2009.
2.Борисов В.В., Круглов В.В., Федулов А.С. Нечеткие модели и сети. М.: Горячая линия — Телеком, 2007.
3.Вавилов А.А. Структурный и параметрический синтез сложных систем. Л.: ЛЭТИ, 1979.
4.Вавилов А.А., Имаев Д.X. Эволюционный синтез систем управления. Л.: ЛЭТИ, 1983.
5.Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. 4-е издание, переработанное и дополненное. Москва: Финансы и Статистика, 2002.
6.Кобзарь А.И. Прикладная математическая статистика. М.: Физматлит, 2006.
7.Кораблев Ю.А., Шестопалов М.Ю. Идентификация технологических процессов и управление ими на основе FUZZY- и NEURO-FUZZY-технологий: Учебное пособие. СПб.: изд-во СПбГЭТУ «ЛЭТИ», 2007.
8.Корнилова Т.В., Шуранова О.И. Корреляционные исследования: пути приближения к причинному анализу. Becтн. Моск. ун-та. Сер. 14, Психология. 1987. № 4.
9.Прикладные нечеткие системы: Перевод с япон. /К. Асаи, Д. Ватада, С. Иваи и др.; под. ред. Т. Тэрано, К. Асаи, М. Сугено. М.: Мир, 1993.
10.Kosko B. Fuzzy Cognitive Maps // Int. Journal of Man-Machine Studies. 1986. V. 24. P. 65—75.
дипломов

Оставить комментарий