СВЯЗЬ МЕЖДУ ТЕРМИЧЕСКИМИ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ ДЛЯ МНОГОСЛОЙНЫХ КОНСТРУКЦИЙ ИЗ ПОЛИМЕРНЫХ МАТЕРИАЛОВ

Фазлутдинова Татьяна Евгеньевна

аспирант 2 курса ОГПУ, г. Оренбург

E-mail: ucheba_v_ogpu@mail.ru

Связь между температурными напряжениями и деформациями проста и вытекает непосредственно из следующего определения. Термические напряжения – напряжения, возникающие в связи с изменением теплового состояния тел при их нагреве, охлаждении, а также длительном пребывании при повышенной или пониженной температуре. Действие термических напряжений состоит, например, в разрушении (растрескивании) при полимеризации, оно может проявляться не в момент изменения теплового состояния (охлаждения), а спустя некоторое время (иногда спустя несколько суток) в результате постепенного накопления напряжений, возникающих при изменении удельных объемов структурных составляющих.

Исследуемая связь хорошо отражена в теории линейной вязко-упругости (наследственности), развитой Больцманом, Вольтера, Работновым и получившей широкое распространение в последнее время. Одной из основных гипотез данной теории является гипотеза о затухающей памяти, подробно обсужденная в книге Кристенсена [3].

Гипотеза о затухающей памяти принималась безоговорочно для полимерных тел до тех пор, пока Фитцджеральдом не был указан класс полимерных материалов и описан ряд опытов на них, для которых гипотеза о затухающей памяти не подтверждается, — это наполненные тонко дисперсными минеральными частицами эластомеры. Под незатухающей памятью обычно понимается свойство материала накапливать при действии напряжений некоторые необратимые изменения, не исчезающие далее под действием времени [5]. Определить же линейно-упругую вязкость можно следующим образом. Если напряжение σ, определяемое как функция от ε, изменяется для некоторого тела с изменением ε так, что удовлетворяются равенства

σ(С∙ε) = С∙σ(ε)                                            (1)

и (или)

σ(ε₁+ε₂)=σ(ε₁)+σ(ε₂)                                        (2)

(С – постоянная величина, ε(t₁) и ε(t₂) - законы изменения деформаций во времени t), то такое тело есть линейное вязко – упругое. Условие (1) Фитцджеральд называет условием однородности. Это название соответствует определению однородной функции, данной Смирновым, согласно которому функция любого числа переменных называется однородной функцией этих переменных степени m, если при умножении всех этих переменных на произвольную величину t функция умножается на число, равное t^m. Из этого определения видно, что удовлетворяющая условию (1) функция есть однородность первой степени.

Условие (2) есть математическое выражение принципа линейной суперпозиции (наложения) [1].

Отечественными исследователями Трифоновым и Малининым, показано что для некоторых материалов, обнаруживающих свойство незатухающей памяти, при не слишком высоких напряжениях удовлетворяется условие (1), а условие (2) существенно не удовлетворяется [3]. Такого типа поведение  названо этими авторами полулинейным, для описания полулинейного поведения известные теории линейной и нелинейной вязко-упругости непригодны.

Зададимся целью получить уравнения связи между напряжениями и деформациями для материала, для которого в частном случае удовлетворяется условие (1), но не удовлетворяется условие (2).

Сформулируем следующие гипотезы:

1.  При макроскопической деформации ε деформации в различных микрообъемах (или для полимерного материала деформации цепи) ε могут быть разными и при этом существует связь между ε₁ и ε₂:

ε₁ = η₁∙ε,                                                      (3)

где η₁ - некоторый коэффициент, который можно назвать коэффициентом концентрации деформации. Наличие концентрации деформации может быть вызвано влиянием частиц наполнителя, а также разнодлинностью цепей полимера при полимеризации.

2.  В процессе деформирования в микрообъемах возникают повреждения π_i, определяемые соотношением:

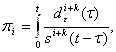                                                   (4)

где t - время, s(t) - деформация при разрушении в функции времени t в опыте на релаксацию напряжений, k - параметр. Критерий разрушения представляет собой обобщение на нелинейный случай предложенного А. А. Ильюшиным линейного критерия [4], где последний записан в деформациях.

3.  Для всех микрообъемов (или для всех цепей) существует один и тот же закон связи между микронапряжениями σ₁ и деформациями ε₁

                                   (5)

4.  Функция s(t) есть степенная

s(t) = A∙t^-m ,                                                 (6)

где A и m – параметры.

Из (4) с учетом (3) и (6) устанавливаем связь между η₁ и π₁

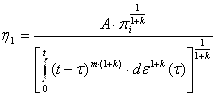.                                      (7)

Для простоты функционал, стоящий в знаменателе правой части этой формулы, будем обозначать F[ε(τ)] или F[ε], т.е.

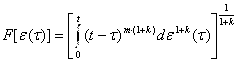.                                  (8)

Более правильным было бы обозначение , однако, в связи с тем, что в F[ε] в нижнем и верхнем пределах τ всегда будет 0 и t, писать их не будем.

В момент разрушения π_i=1 и максимальная величина η_i, для которой в момент t произошло разрушение, будет равна величине η_c, определяемой отношением

                                                  (9)

С учетом (9) гипотеза (3) может быть записана в виде

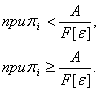                              (10)

Величину η_c можно считать запасом прочности полимера; при η_c =1 происходит разрушение образца [2].

Рассматриваемое напряжение σ, с учетом изложенного, можно записать в виде:

                                      (11)

Здесь в качестве нижнего предела коэффициента η, характеризующего концентрацию деформации мягкого связующего в зазоре между жесткими частицами, принята единица. В самом деле, если бы жесткие частицы отсутствовали, то можно было бы считать η=1 по всему объему полимера. При наличии жестких частиц можно предполагать все же в каких-то объемах полимера, на большем удалении от частиц наполнителя существование областей, где η≈1. Кроме того, как было показано ранее, при снижении η_c до 1 происходит разрушение образца. Весовая функция N(η) определяет вклад в величину σ тех областей, для которых коэффициент η находится от η до η +d η.

По поводу функции N(η) можно утверждать следующее. Разложим ее в ряд Лорана

                                             (12)

Поскольку N(η) должна удовлетворять условиям нормирования , то члены в ряде Лорана, для которых i ≥ -1, должны обращаться в нуль, чтобы ряд (12) был абсолютно сходящимся. Ограничиваясь членами ряда (12), при этом имеем:

                                                (13)

Можно предполагать, что функция σ=f(ηε) есть монотонная возрастающая функция при не слишком больших деформациях многослойной конструкции. Разлагая ее в ряд Тейлора  с учетом того, что f(0)=0  из (11) с учетом (9) имеем:

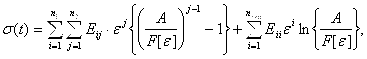                 (14)

где E_ij и E_ii – постоянные, n_min – минимальная из n₁, n₂.

Соотношение (14) в том виде, как оно здесь приведено, использовать сложно, поэтому для практических применений будет частный случай (14), который можно записать в виде:

                          (15)

Существует ряд неравенств, предложенных еще Фитцджеральдом, важных для понимания поведения полимерного материала, причем они имеют место при k≥0 и для функционала F[ε] при условии, что или ε₁ в (4) всегда больше нуля, или, если ε₁ - отрицательна, то берется ее абсолютное значение.

Эти неравенства имеют вид:

F[ε₁∙ε₂]≤F[ε₁]∙F[ε₂].                                       (16)

F[ε₁+ε₂]≤F[ε₁]+F[ε₂].                                      (17)

F[ε₁-ε₂]≤F[ε₁-ε₃]∙F[ε₃-ε₂].                                   (18)

Справедливо также равенство:

F[c∙ε₁]=c∙F[ε₁] (c=const) .                                  (19)

Равенство (19) с учетом (8) доказывается путем несложных преобразований, неравенство (18) вытекает из (17), а для доказательства неравенства (17) используется неравенство Минковского

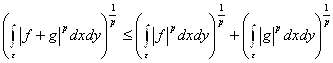.                      (20)

Интегрируя по частям с учетом того, что k≤0 и m>0, имеем:

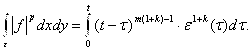
Далее полагаем:

|f|=ε₁, |g|=ε₂, τ=x, p=1+k . Интегрирование ведем в области ε, ограниченной осью абсцисс, ординатой x=t и графиком y=(t-τ)^m(1+k)-1. Например, для ε₁ при этом имеем:

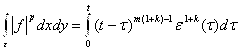, и из (20) имеем (17).

Из неравенства (17) и равенства (19) мы можем получить в частном случае поведение материала такое, что условие однородности (1) удовлетворяется, а принцип суперпозиции (2) не удовлетворяется. Ограничимся для простоты в (15) двумя членами в правой части. Пусть имеем законы деформирования: первый, когда ε=ε(t) и второй, когда ε=c∙ε(t) (c=const). Из (15) видно, что в любой момент времени t напряжения σ будут во втором случае в c раз больше, чем в первом.

Теперь ограничимся в (15) двумя первыми членами в правой части. Представим себе, что рассматриваются два закона деформирования, когда деформации и напряжения в функции времени были ε₁(t), ε₂(t) и σ₁(t), σ₂(t), а также третий закон, когда ε₃(t)=ε₁(t)+ε₂(t). Найдем σ₃ по формуле (15), где удержаны два члена разложения. Имеем:

.                                             (21)

Поскольку в (17) F[ε₁+ε₂]≤F[ε₁]+F[ε₂], а нас здесь может интересовать лишь знак «больше», то из (21) в общем случае будем имеет

σ₃(t)>σ₁(t)+σ₂(t).                                                       (22)

Иллюстрация неравенства (22) приведена в работе [4]. В проводимых опытах всегда получалось, что фактическое напряжение было всегда больше расчетного, определенного с помощью принципа суперпозиции, так что экспериментальная кривая в координатах σ0ε при больших t в опыте с задержкой приближалась к диаграмме, снятой в опыте без задержки.

Список литературы.

1.Акимов И.А., Акимов А.И. Математическое описание теплофизических процессов полимеризации.// Санкт-Петербург. Изд.-во СПбГПУ. Формирование технологической политики инновационных наукоемких технологий. Материалы научно-технической конференции и школы семинара. — 2003. — С. 299 — 306.

2.Акимов И.А., Акимов А.И., Инчин А.Н. Теоретические и экспериментальные исследования технологического процесса изготовления изделий из композиционных материалов. // Препринт. – Уфа: Редакционно-издательский центр Башгосуниверситета, 2003. — 38 с.

3.Вигак В.М. Управление температурными напряжениями и перемещениями. Киев: Наукова Думка, 1988 — 313 с.

4.Ильюшин А.А. Об одной теории длительной прочности. — Изв. АН СССР, «Механика твердого тела», 1967, № 3, с. 21 — 35

5.Кутателадзе С.С. Основы теории теплообмена. – Изд. 5-е перераб. И доп. — М.: Атомиздат, 1979, — 416 с.

6.Лыков А.В. Теория теплопроводности. – М., «Высшая школа», 1967 — 599 с.